
Question and Answers Forum
Question Number 123859 by sdfg last updated on 28/Nov/20
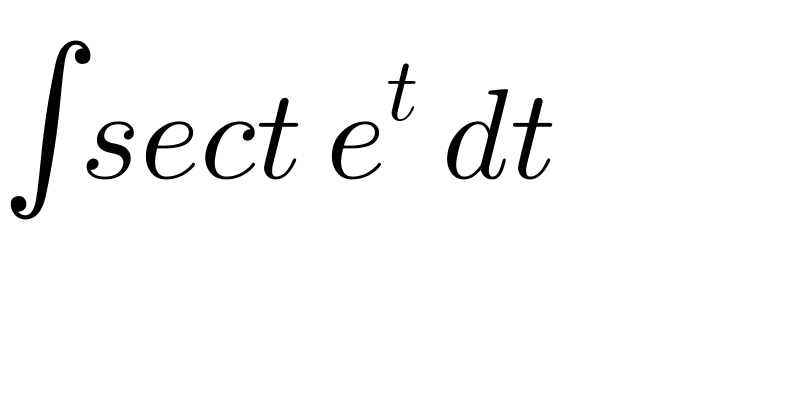
Answered by mindispower last updated on 29/Nov/20
![sec(x)=(2/(e^(ix) +e^(−ix) )),we use cos(x)=((e^(ix) +e^(−ix) )/2) =((2e^(ix) )/(1+e^(2ix) ))=2Σ_(n≥0) (−1)^n e^((2n+1)ix) ∫sec(x)e^x dx=2∫Σ_(n≥0) (−1)^n e^((2n+1)ix+x) dx 2Σ_(n≥0) (−1)^n ∫e^((2n+1)ix+x) dx =2Σ_(n≥0) (−1)^n (e^(((2n+1)i+1)x) /((2n+1)i+1))+c =2e^((1+i)x) Σ_(n≥0) (((−e^(2ix) )^n )/((2n+1)i+1)) =2e^((1+i)x) Σ_(n≥0) ((−i(−e^(2ix) )^n )/(2n+1−i))=e^((1+i)x) Σ_(n≥0) (((−i)(−e^(2ix) )^n )/(n+(((1−i)/2)))) =e^((1+i)x) Σ_(n≥0) (((−i)(−e^(2ix) )^n )/(n!)).((n!)/(n+(((1−i)/2)))) =e^((1+i)x) (((−2i)/(1−i))+Σ_(n≥1) (((−i)(−e^(2ix) )^n .Π_(k=0) ^(n−1) (k+(((1−i)/2)).Π_(k=0) ^(n−1) (1+k))/(Π_(k=0) ^(n−1) (k+(((3−i)/2))).(((1−i)/2)))) =−((2i)/(1−i))e^((1+i)x) (1+((1−i)/(−2i))Σ_(n≥1) (((−i))/((((1−i)/2)))).(((((1−i)/2))_n (1)_n )/((((3−i)/2))_n )).(((−e^(2ix) )^n )/(n!))) =(1−i)e^((1+i)x) (1+Σ_(n≥1) (((((1−i)/2))_n (1)_n )/((((3−i)/2))_n )).(((−e^(2ix) )^n )/(n!)))+c (a)_n =Π_(k=0) ^(n−1) (a+k),n!=1......n=(1+0)....(1+(n−1)) =(1)_n ....we used this all long now use 2F_1 (a,b;c;[x])=(1+Σ_(n≥1) (((a_n )(b)_n )/((c)_n )).(x^n /(n!))) we get =(1−i)e_ ^((1+i)x) _2 F_1 (((1−i)/2),1;((3−i)/2),[−e^(2ix) ])+C C constante ∫sec(x)e^x dx=(1−i)e^((1+i)x) _2 F_1 (((1−i)/2),1,((3−i)/2);[−e^(2ix) ])+C [X] is argument of function not floor function](Q123897.png)
| ||
Question and Answers Forum | ||
Question Number 123859 by sdfg last updated on 28/Nov/20 | ||
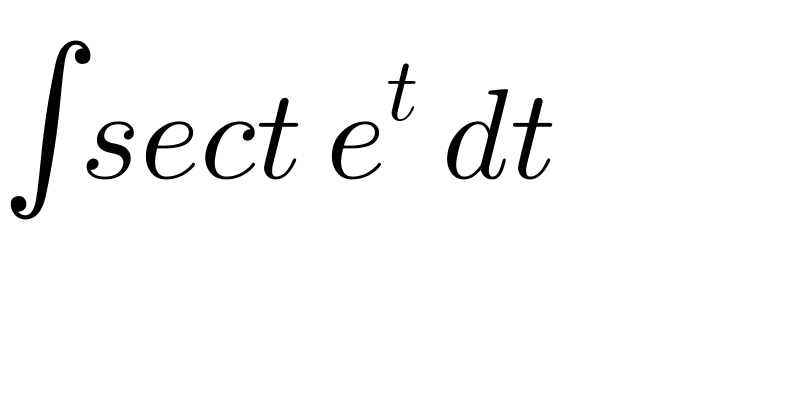 | ||
Answered by mindispower last updated on 29/Nov/20 | ||
![sec(x)=(2/(e^(ix) +e^(−ix) )),we use cos(x)=((e^(ix) +e^(−ix) )/2) =((2e^(ix) )/(1+e^(2ix) ))=2Σ_(n≥0) (−1)^n e^((2n+1)ix) ∫sec(x)e^x dx=2∫Σ_(n≥0) (−1)^n e^((2n+1)ix+x) dx 2Σ_(n≥0) (−1)^n ∫e^((2n+1)ix+x) dx =2Σ_(n≥0) (−1)^n (e^(((2n+1)i+1)x) /((2n+1)i+1))+c =2e^((1+i)x) Σ_(n≥0) (((−e^(2ix) )^n )/((2n+1)i+1)) =2e^((1+i)x) Σ_(n≥0) ((−i(−e^(2ix) )^n )/(2n+1−i))=e^((1+i)x) Σ_(n≥0) (((−i)(−e^(2ix) )^n )/(n+(((1−i)/2)))) =e^((1+i)x) Σ_(n≥0) (((−i)(−e^(2ix) )^n )/(n!)).((n!)/(n+(((1−i)/2)))) =e^((1+i)x) (((−2i)/(1−i))+Σ_(n≥1) (((−i)(−e^(2ix) )^n .Π_(k=0) ^(n−1) (k+(((1−i)/2)).Π_(k=0) ^(n−1) (1+k))/(Π_(k=0) ^(n−1) (k+(((3−i)/2))).(((1−i)/2)))) =−((2i)/(1−i))e^((1+i)x) (1+((1−i)/(−2i))Σ_(n≥1) (((−i))/((((1−i)/2)))).(((((1−i)/2))_n (1)_n )/((((3−i)/2))_n )).(((−e^(2ix) )^n )/(n!))) =(1−i)e^((1+i)x) (1+Σ_(n≥1) (((((1−i)/2))_n (1)_n )/((((3−i)/2))_n )).(((−e^(2ix) )^n )/(n!)))+c (a)_n =Π_(k=0) ^(n−1) (a+k),n!=1......n=(1+0)....(1+(n−1)) =(1)_n ....we used this all long now use 2F_1 (a,b;c;[x])=(1+Σ_(n≥1) (((a_n )(b)_n )/((c)_n )).(x^n /(n!))) we get =(1−i)e_ ^((1+i)x) _2 F_1 (((1−i)/2),1;((3−i)/2),[−e^(2ix) ])+C C constante ∫sec(x)e^x dx=(1−i)e^((1+i)x) _2 F_1 (((1−i)/2),1,((3−i)/2);[−e^(2ix) ])+C [X] is argument of function not floor function](Q123897.png) | ||
| ||