
Question and Answers Forum
Question Number 123874 by john_santu last updated on 29/Nov/20

Answered by liberty last updated on 29/Nov/20
![solve this question (1) lim_(θ→0) ((θ−sin θcos θ)/(tan θ−θ)) (2) lim_(x→0) ((sin 3x−3x+x^2 )/(sin x sin 2x)) Solution : (1) by L′Hopital rule lim_(θ→0) ((θ−(1/2)sin 2θ)/(tan θ−θ)) = lim_(θ→0) ((1−cos 2θ)/(sec^2 θ−1)) lim_(θ→0) ((cos^2 θ(2sin^2 ((θ/2))))/(sin^2 θ)) = lim_(θ→0) 2(((sin (θ/2))/(tan θ)))^2 = (1/2) (2) lim_(x→0) ((sin 3x−3x+x^2 )/(−(1/2)(cos 3x−cos x))) = −2×lim_(x→0) ((3cos 3x−3+2x)/(−3sin 3x+sin x)) = −2×lim_(x→0) ((−9sin 3x+2)/(−9cos 3x+cos x)) = −2× [(2/(−8)) ] = (1/2).](Q123875.png)
Answered by Dwaipayan Shikari last updated on 29/Nov/20
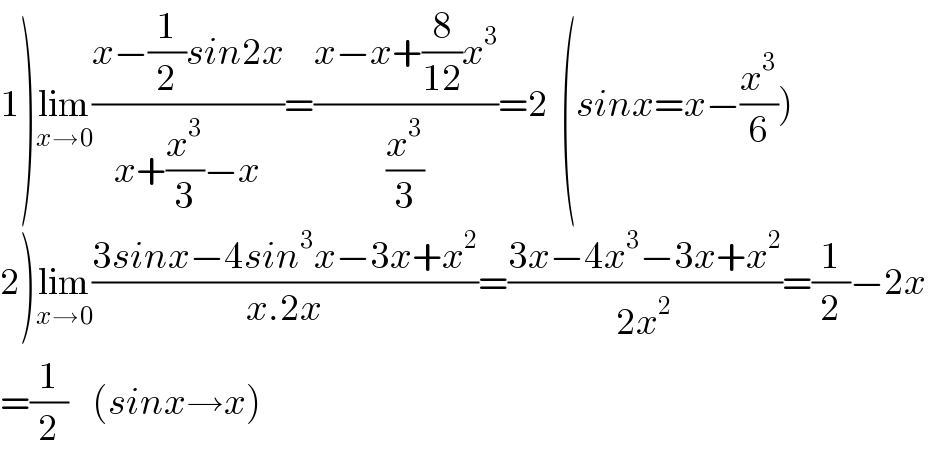
| ||
Question and Answers Forum | ||
Question Number 123874 by john_santu last updated on 29/Nov/20 | ||
 | ||
Answered by liberty last updated on 29/Nov/20 | ||
![solve this question (1) lim_(θ→0) ((θ−sin θcos θ)/(tan θ−θ)) (2) lim_(x→0) ((sin 3x−3x+x^2 )/(sin x sin 2x)) Solution : (1) by L′Hopital rule lim_(θ→0) ((θ−(1/2)sin 2θ)/(tan θ−θ)) = lim_(θ→0) ((1−cos 2θ)/(sec^2 θ−1)) lim_(θ→0) ((cos^2 θ(2sin^2 ((θ/2))))/(sin^2 θ)) = lim_(θ→0) 2(((sin (θ/2))/(tan θ)))^2 = (1/2) (2) lim_(x→0) ((sin 3x−3x+x^2 )/(−(1/2)(cos 3x−cos x))) = −2×lim_(x→0) ((3cos 3x−3+2x)/(−3sin 3x+sin x)) = −2×lim_(x→0) ((−9sin 3x+2)/(−9cos 3x+cos x)) = −2× [(2/(−8)) ] = (1/2).](Q123875.png) | ||
| ||
Answered by Dwaipayan Shikari last updated on 29/Nov/20 | ||
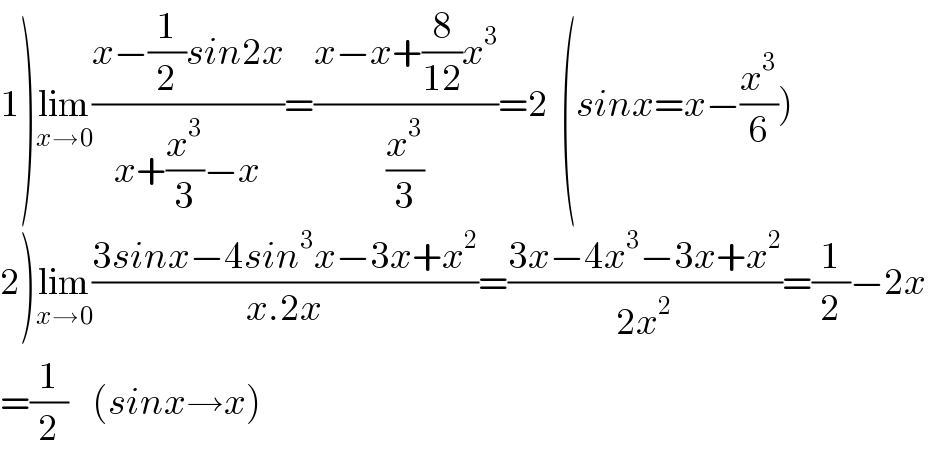 | ||
| ||