Question Number 123900 by mnjuly1970 last updated on 29/Nov/20
$$\:\:\:\:\:\:\:\:\:...\:{advanced}\:\:{integral}... \\ $$$$\:\:\:{prove}\:\:{that}\::: \\ $$$$\:\:\:\:\:\:\Omega=\int_{\mathrm{0}} ^{\:\infty} \frac{{sin}^{\mathrm{2}} \left({x}\right)}{{x}^{\mathrm{2}} \left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx}\:=\frac{\pi}{\mathrm{4}}\left(\mathrm{1}+\frac{\pi}{{e}^{\mathrm{2}} }\right) \\ $$
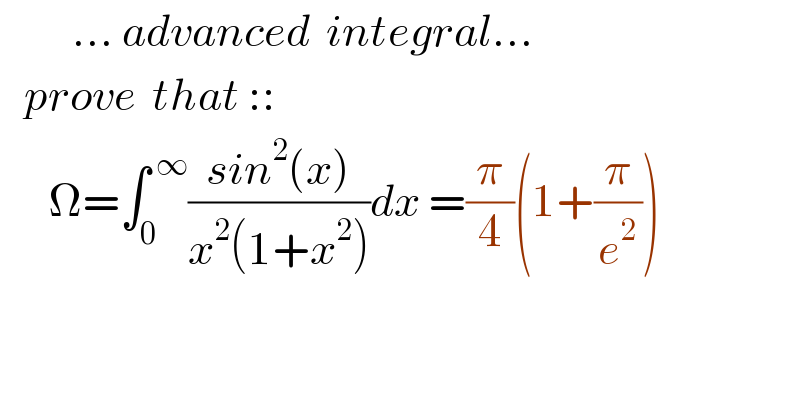
Answered by mathmax by abdo last updated on 29/Nov/20
![I=∫_0 ^∞ ((sin^2 x)/(x^2 (1+x^2 )))dx ⇒I =∫_0 ^∞ ((1/x^2 )−(1/(1+x^2 )))sin^2 x dx =∫_0 ^∞ ((sin^2 x)/x^2 )−∫_0 ^∞ ((sin^2 x)/(x^2 +1))dx we have by[psrts ∫_0 ^∞ ((sin^2 x)/x^2 )dx =[−((sin^2 x)/x)]_0 ^∞ +∫_0 ^∞ ((2sinx cosx)/x)dx =∫_0 ^∞ ((sin(2x))/x)dx =_(2x=t) ∫_0 ^∞ ((sin(t))/(t/2))(dt/2)=∫_0 ^∞ ((sint)/t)dt=(π/2) ∫_0 ^∞ ((sin^2 x)/(x^2 +1))dx =∫_0 ^∞ ((1−cos(2x))/(2(x^2 +1)))dx =(1/2)∫_0 ^∞ (dx/(x^2 +1))−(1/2)∫_0 ^∞ ((cos(2x))/(x^2 +1))dx =(π/4)−(1/2)∫_0 ^∞ ((cos(2x))/(x^2 +1))dx we have ∫_0 ^∞ ((cos(2x))/(x^2 +1))dx =(1/2)Re(∫_(−∞) ^(+∞) (e^(2ix) /(x^2 +1))dx) ∫_(−∞) ^(+∞) (e^(2ix) /(x^2 +1))dx =2iπ×(e^(−2) /(2i)) =(π/e^2 ) ⇒∫_0 ^∞ ((cos(2x))/(x^2 +1))dx=(π/(2e^2 )) ⇒ I =(π/2)−(π/4) +(1/2).(π/(2e^2 )) =(π/4)+(π/(4e^2 )) =(π/4)(1+(1/e^2 ))](Q123916.png)
$$\mathrm{I}=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}\mathrm{dx}\:\Rightarrow\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)\mathrm{sin}^{\mathrm{2}} \mathrm{x}\:\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}^{\mathrm{2}} }−\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{by}\left[\mathrm{psrts}\right. \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:=\left[−\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}}\right]_{\mathrm{0}} ^{\infty} +\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2sinx}\:\mathrm{cosx}}{\mathrm{x}}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sin}\left(\mathrm{2x}\right)}{\mathrm{x}}\mathrm{dx}\:=_{\mathrm{2x}=\mathrm{t}} \:\:\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sin}\left(\mathrm{t}\right)}{\frac{\mathrm{t}}{\mathrm{2}}}\frac{\mathrm{dt}}{\mathrm{2}}=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sint}}{\mathrm{t}}\mathrm{dt}=\frac{\pi}{\mathrm{2}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}\:=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)}\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx} \\ $$$$=\frac{\pi}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Re}\left(\int_{−\infty} ^{+\infty} \:\frac{\mathrm{e}^{\mathrm{2ix}} }{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx}\right) \\ $$$$\int_{−\infty} ^{+\infty} \:\frac{\mathrm{e}^{\mathrm{2ix}} }{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx}\:=\mathrm{2i}\pi×\frac{\mathrm{e}^{−\mathrm{2}} }{\mathrm{2i}}\:=\frac{\pi}{\mathrm{e}^{\mathrm{2}} }\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}=\frac{\pi}{\mathrm{2e}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{I}\:=\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{2}}.\frac{\pi}{\mathrm{2e}^{\mathrm{2}} }\:=\frac{\pi}{\mathrm{4}}+\frac{\pi}{\mathrm{4e}^{\mathrm{2}} }\:=\frac{\pi}{\mathrm{4}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{e}^{\mathrm{2}} }\right) \\ $$
Commented by mnjuly1970 last updated on 29/Nov/20
$${grateful}\:{my}\:{master}\:{sir}\:{max} \\ $$
Commented by mathmax by abdo last updated on 29/Nov/20
$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome}\:\mathrm{sir} \\ $$
Answered by mindispower last updated on 29/Nov/20
![Ω=∫_0 ^∞ (((1+x^2 −x^2 )sin^2 (x)dx)/(x^2 (1+x^2 ))) ∫((sin^2 (x))/x^2 )−∫_0 ^∞ ((sin^2 (x))/(1+x^2 ))dx sin^2 (x)=((1−cos(2x))/2) Ω=∫((sin^2 (x))/x_(=A) ^2 )−∫(dx/(2(1+x^2 )))+(1/2)∫_0 ^∞ ((cos(2x))/(1+x^2 ))dx A by part [−((sin^2 (x))/x)]_0 ^∞ +∫_0 ^∞ ((sin(2x))/x)dx =∫_0 ^∞ 2.sin(2x).(dx/(2x))=∫_0 ^∞ ((sin(t))/t)dt=(π/2) ∫_0 ^∞ (dx/(2(1+x^2 )))=(1/2)arctan(x)]_0 ^∞ =(π/4) Ω=(π/2)−(π/4)+(1/2)∫((cos(2x))/(1+x^2 ))dx(π/4)+(1/2)B B=(1/2)∫_(−∞) ^∞ ((cos(2x))/(1+x^2 ))dx=(1/2)Re∫_(−∞) ^∞ (e^(2ix) /(1+x^2 ))dx =(1/2).2iπRes((e^(2ix) /(1+x^2 )),x=i{ =iπ(e^(−2) /(2i))=(π/e^2 ) Ω=(π/4)+.(1/2)(π/(2e^2 ))=(π/4)(1+(1/e^2 ))](Q123905.png)
$$\Omega=\int_{\mathrm{0}} ^{\infty} \frac{\left(\mathrm{1}+{x}^{\mathrm{2}} −{x}^{\mathrm{2}} \right){sin}^{\mathrm{2}} \left({x}\right){dx}}{{x}^{\mathrm{2}} \left(\mathrm{1}+{x}^{\mathrm{2}} \right)} \\ $$$$\int\frac{{sin}^{\mathrm{2}} \left({x}\right)}{{x}^{\mathrm{2}} }−\int_{\mathrm{0}} ^{\infty} \frac{{sin}^{\mathrm{2}} \left({x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$${sin}^{\mathrm{2}} \left({x}\right)=\frac{\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}} \\ $$$$\Omega=\int\frac{{sin}^{\mathrm{2}} \left({x}\right)}{{x}_{={A}} ^{\mathrm{2}} }−\int\frac{{dx}}{\mathrm{2}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{cos}\left(\mathrm{2}{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$${A}\:{by}\:{part} \\ $$$$\left[−\frac{{sin}^{\mathrm{2}} \left({x}\right)}{{x}}\right]_{\mathrm{0}} ^{\infty} +\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left(\mathrm{2}{x}\right)}{{x}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \mathrm{2}.{sin}\left(\mathrm{2}{x}\right).\frac{{dx}}{\mathrm{2}{x}}=\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left({t}\right)}{{t}}{dt}=\frac{\pi}{\mathrm{2}} \\ $$$$\left.\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\mathrm{2}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}=\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left({x}\right)\right]_{\mathrm{0}} ^{\infty} =\frac{\pi}{\mathrm{4}} \\ $$$$\Omega=\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{cos}\left(\mathrm{2}{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\frac{\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}{B} \\ $$$${B}=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{\infty} \frac{{cos}\left(\mathrm{2}{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}=\frac{\mathrm{1}}{\mathrm{2}}{Re}\int_{−\infty} ^{\infty} \frac{{e}^{\mathrm{2}{ix}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{2}{i}\pi{Res}\left(\frac{{e}^{\mathrm{2}{ix}} }{\mathrm{1}+{x}^{\mathrm{2}} },{x}={i}\left\{\right.\right. \\ $$$$={i}\pi\frac{{e}^{−\mathrm{2}} }{\mathrm{2}{i}}=\frac{\pi}{{e}^{\mathrm{2}} } \\ $$$$\Omega=\frac{\pi}{\mathrm{4}}+.\frac{\mathrm{1}}{\mathrm{2}}\frac{\pi}{\mathrm{2}{e}^{\mathrm{2}} }=\frac{\pi}{\mathrm{4}}\left(\mathrm{1}+\frac{\mathrm{1}}{{e}^{\mathrm{2}} }\right) \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 29/Nov/20
$${thanks}\:{alot}\:{sir}\:{mindspower} \\ $$$$\:{nice}\:\:{as}\:{always}... \\ $$
Commented by mindispower last updated on 29/Nov/20
$${withe}\:{pleasur}\: \\ $$$${sad}\:{not}\:{times}\:{too}\:{do}\:{maths}\:{these}\:{days} \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 29/Nov/20
$${i}\:{hope}\:{you}\:{are}\:{successful} \\ $$$${in}\:{all}\:{stages}\:{of}\:{your}\:{life}\: \\ $$$${god}\:\:{keep}\:\:{you}.. \\ $$