
Question and Answers Forum
Question Number 123920 by john_santu last updated on 29/Nov/20
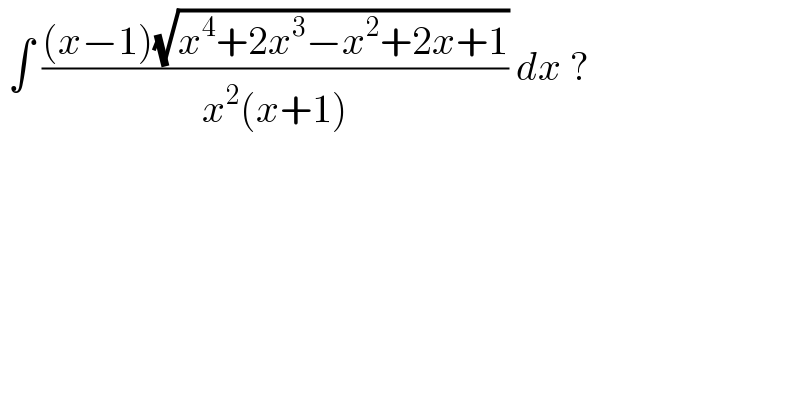
Answered by liberty last updated on 29/Nov/20
![(•) ((x−1)/(x^2 (x+1))) = ((x^2 −1)/(x^2 (x+1)^2 )) =(1−(1/x^2 ))((1/(x^2 (x+(1/x)+2)))) (••) x^4 +2x^3 −x^2 +2x+1=x^2 (x^2 +(1/x^2 )+2(x+(1/x))−1) = x^2 ((x+(1/x))^2 +2(x+(1/x))−3)=x^2 ((x+(1/x)+1)^2 −4) letting 2sec v = x+(1/x)+1 T=∫ ((√(4sec^2 v−4))/(2sec v+1)) (2sec v tan v )dv T=∫ ((4tan^2 v sec v )/(2sec v +1)) dv = ∫(2sec^2 v−sec v)dv−∫((3sec v dv)/(2sec v +1)) T= 2tan v −ℓn ∣sec v + tan v∣ −∫ ((3(2−cos v))/(4−cos^2 v)) dv let L=∫ ((6−3cos v)/(4−cos^2 v)) dv = ∫ ((6sec^2 v)/(4sec^2 v−1))dv−∫((3cos v)/(3+sin^2 v)) dv L=∫ ((6du)/(4u^2 +3)) [ u = tan v ] −∫((3dj)/(3+j^2 )) [ j = sin v ] L= (√3) tan^(−1) (((2u)/( (√3))))−(√3) tan^(−1) ((j/( (√3)))) L= (√3) tan^(−1) (((2tan v)/( (√3))))−(√3) tan^(−1) (((sin v)/( (√3)))) Thus T = 2tan v −ℓn∣sec v + tan v ∣− (√3) {tan^(−1) (((2tan v)/( (√3))))−tan^(−1) (((sin v)/( (√3))))}+ c where v = sec^(−1) (((x^2 +x+1)/(2x))) .](Q123923.png)
Answered by MJS_new last updated on 29/Nov/20
![∫(((x−1)(√(x^4 +2x^3 −x^2 +2x+1)))/(x^2 (x+1)))dx= =∫(((x−1)(√((x^2 −x+1)(x^2 +3x+1))))/(x^2 (x+1)))dx= [t=((√(x^2 −x+1))/( (√(x^2 +3x+1)))) → dx=(((x^2 +3x+1)^(3/2) (√(x^2 −x+1)))/(2(x^2 −1)))dt] =32∫(t^2 /(t^6 +t^4 −5t^2 +3))dt= =32∫(t^2 /((t−1)^2 (t+1)^2 (t^2 +3)))dt= =2∫(dt/((t−1)^2 ))+2∫(dt/((t+1)^2 ))−6∫(dt/(t^2 +3))+∫(dt/(t−1))−∫(dt/(t+1))= =−(2/(t−1))−(2/(t+1))−2(√3)arctan (((√3)t)/3) +ln (t−1) −ln (t+1) = =−((4t)/(t^2 −1))−2(√3)arctan (((√3)t)/3) +ln ((t−1)/(t+1)) = =((√((x^2 −x+1)(x^2 +3x+1)))/x)−2(√3)arctan ((√(3(x^2 −x+1)))/(3(√(x^2 +3x+1)))) +ln ∣((x^2 +x+1−(√((x^2 −x+1)(x^2 +3x+1))))/(2x))∣ +C](Q123935.png)
Commented by liberty last updated on 29/Nov/20

| ||
Question and Answers Forum | ||
Question Number 123920 by john_santu last updated on 29/Nov/20 | ||
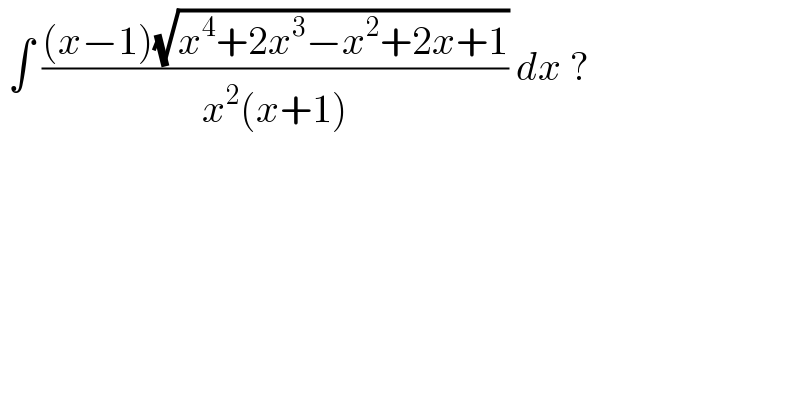 | ||
Answered by liberty last updated on 29/Nov/20 | ||
![(•) ((x−1)/(x^2 (x+1))) = ((x^2 −1)/(x^2 (x+1)^2 )) =(1−(1/x^2 ))((1/(x^2 (x+(1/x)+2)))) (••) x^4 +2x^3 −x^2 +2x+1=x^2 (x^2 +(1/x^2 )+2(x+(1/x))−1) = x^2 ((x+(1/x))^2 +2(x+(1/x))−3)=x^2 ((x+(1/x)+1)^2 −4) letting 2sec v = x+(1/x)+1 T=∫ ((√(4sec^2 v−4))/(2sec v+1)) (2sec v tan v )dv T=∫ ((4tan^2 v sec v )/(2sec v +1)) dv = ∫(2sec^2 v−sec v)dv−∫((3sec v dv)/(2sec v +1)) T= 2tan v −ℓn ∣sec v + tan v∣ −∫ ((3(2−cos v))/(4−cos^2 v)) dv let L=∫ ((6−3cos v)/(4−cos^2 v)) dv = ∫ ((6sec^2 v)/(4sec^2 v−1))dv−∫((3cos v)/(3+sin^2 v)) dv L=∫ ((6du)/(4u^2 +3)) [ u = tan v ] −∫((3dj)/(3+j^2 )) [ j = sin v ] L= (√3) tan^(−1) (((2u)/( (√3))))−(√3) tan^(−1) ((j/( (√3)))) L= (√3) tan^(−1) (((2tan v)/( (√3))))−(√3) tan^(−1) (((sin v)/( (√3)))) Thus T = 2tan v −ℓn∣sec v + tan v ∣− (√3) {tan^(−1) (((2tan v)/( (√3))))−tan^(−1) (((sin v)/( (√3))))}+ c where v = sec^(−1) (((x^2 +x+1)/(2x))) .](Q123923.png) | ||
| ||
Answered by MJS_new last updated on 29/Nov/20 | ||
![∫(((x−1)(√(x^4 +2x^3 −x^2 +2x+1)))/(x^2 (x+1)))dx= =∫(((x−1)(√((x^2 −x+1)(x^2 +3x+1))))/(x^2 (x+1)))dx= [t=((√(x^2 −x+1))/( (√(x^2 +3x+1)))) → dx=(((x^2 +3x+1)^(3/2) (√(x^2 −x+1)))/(2(x^2 −1)))dt] =32∫(t^2 /(t^6 +t^4 −5t^2 +3))dt= =32∫(t^2 /((t−1)^2 (t+1)^2 (t^2 +3)))dt= =2∫(dt/((t−1)^2 ))+2∫(dt/((t+1)^2 ))−6∫(dt/(t^2 +3))+∫(dt/(t−1))−∫(dt/(t+1))= =−(2/(t−1))−(2/(t+1))−2(√3)arctan (((√3)t)/3) +ln (t−1) −ln (t+1) = =−((4t)/(t^2 −1))−2(√3)arctan (((√3)t)/3) +ln ((t−1)/(t+1)) = =((√((x^2 −x+1)(x^2 +3x+1)))/x)−2(√3)arctan ((√(3(x^2 −x+1)))/(3(√(x^2 +3x+1)))) +ln ∣((x^2 +x+1−(√((x^2 −x+1)(x^2 +3x+1))))/(2x))∣ +C](Q123935.png) | ||
| ||
Commented by liberty last updated on 29/Nov/20 | ||
 | ||