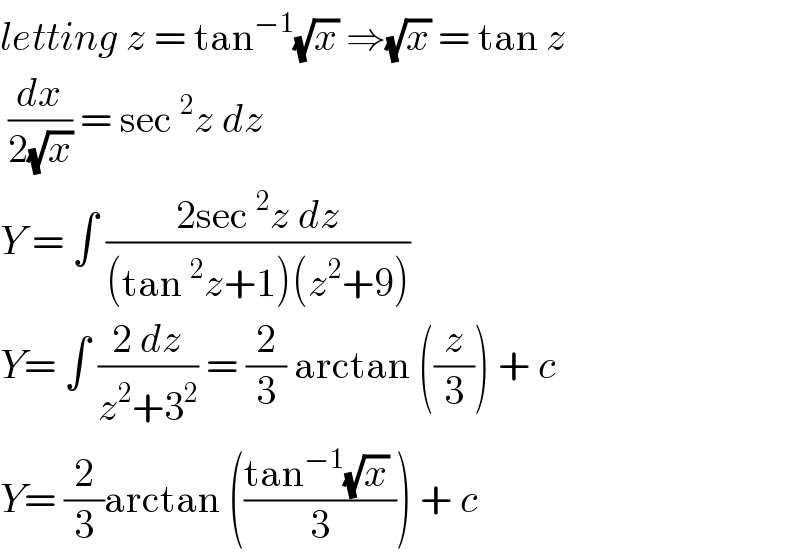Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 123921 by john_santu last updated on 29/Nov/20

∫ (1/( (√x) (x+1)((tan^(−1) (√x))^2 +9)))dx

$$\int\:\frac{\mathrm{1}}{\:\sqrt{{x}}\:\left({x}+\mathrm{1}\right)\left(\left(\mathrm{tan}^{−\mathrm{1}} \sqrt{{x}}\right)^{\mathrm{2}} +\mathrm{9}\right)}{dx} \\ $$

Answered by mindispower last updated on 29/Nov/20

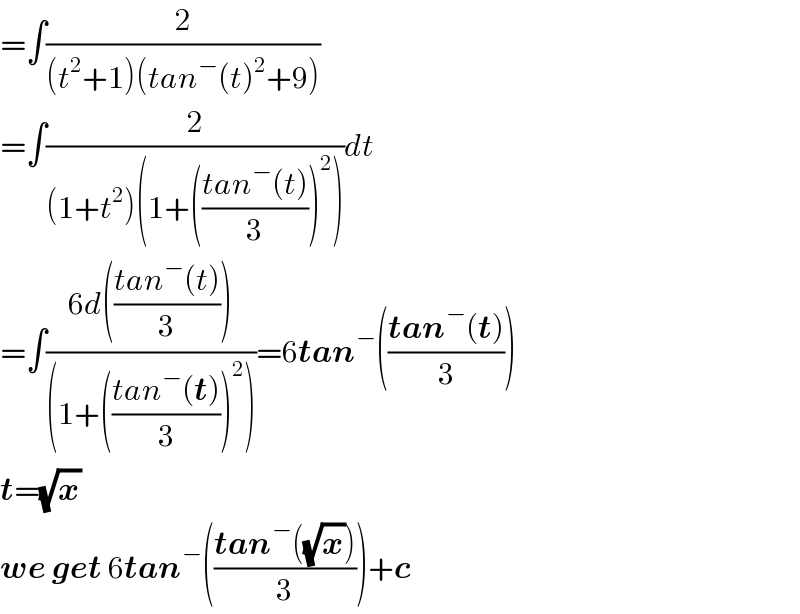
=∫(2/((t^2 +1)(tan^− (t)^2 +9))) =∫(2/((1+t^2 )(1+(((tan^− (t))/3))^2 )))dt =∫((6d(((tan^− (t))/3)))/((1+(((tan^− (t))/3))^2 )))=6tan^− (((tan^− (t))/3)) t=(√x) we get 6tan^− (((tan^− ((√x)))/3))+c

$$=\int\frac{\mathrm{2}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left({tan}^{−} \left({t}\right)^{\mathrm{2}} +\mathrm{9}\right)}\: \\ $$$$=\int\frac{\mathrm{2}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}+\left(\frac{{tan}^{−} \left({t}\right)}{\mathrm{3}}\right)^{\mathrm{2}} \right)}{dt} \\ $$$$=\int\frac{\mathrm{6}{d}\left(\frac{{tan}^{−} \left({t}\right)}{\mathrm{3}}\right)}{\left(\mathrm{1}+\left(\frac{{tan}^{−} \left(\boldsymbol{{t}}\right)}{\mathrm{3}}\right)^{\mathrm{2}} \right)}=\mathrm{6}\boldsymbol{{tan}}^{−} \left(\frac{\boldsymbol{{tan}}^{−} \left(\boldsymbol{{t}}\right)}{\mathrm{3}}\right) \\ $$$$\boldsymbol{{t}}=\sqrt{\boldsymbol{{x}}} \\ $$$$\boldsymbol{{we}}\:\boldsymbol{{get}}\:\mathrm{6}\boldsymbol{{tan}}^{−} \left(\frac{\boldsymbol{{tan}}^{−} \left(\sqrt{\boldsymbol{{x}}}\right)}{\mathrm{3}}\right)+\boldsymbol{{c}} \\ $$

Commented by Mammadli last updated on 29/Nov/20

Commented by liberty last updated on 29/Nov/20

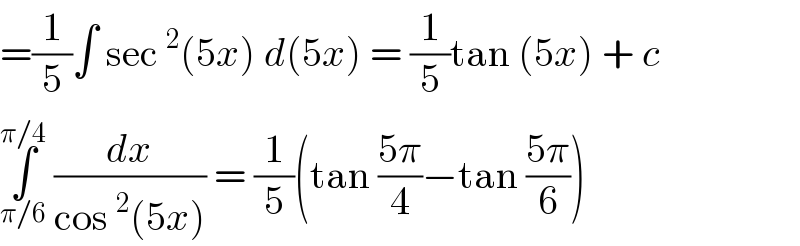
=(1/5)∫ sec^2 (5x) d(5x) = (1/5)tan (5x) + c ∫_(π/6) ^(π/4) (dx/(cos^2 (5x))) = (1/5)(tan ((5π)/4)−tan ((5π)/6))

$$=\frac{\mathrm{1}}{\mathrm{5}}\int\:\mathrm{sec}\:^{\mathrm{2}} \left(\mathrm{5}{x}\right)\:{d}\left(\mathrm{5}{x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{5}}\mathrm{tan}\:\left(\mathrm{5}{x}\right)\:+\:{c}\: \\ $$$$\underset{\pi/\mathrm{6}} {\overset{\pi/\mathrm{4}} {\int}}\:\frac{{dx}}{\mathrm{cos}\:^{\mathrm{2}} \left(\mathrm{5}{x}\right)}\:=\:\frac{\mathrm{1}}{\mathrm{5}}\left(\mathrm{tan}\:\frac{\mathrm{5}\pi}{\mathrm{4}}−\mathrm{tan}\:\frac{\mathrm{5}\pi}{\mathrm{6}}\right) \\ $$

Commented by Dwaipayan Shikari last updated on 29/Nov/20

∫_(π/6) ^(π/4) sec^2 5x dx =(1/5)∫_((5π)/6) ^((5π)/4) sec^2 u du =(1/5)[tanu]_((5π)/6) ^((5π)/4) =(((√3)−1)/(5(√3)))

$$\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{4}}} {sec}^{\mathrm{2}} \mathrm{5}{x}\:{dx}\:=\frac{\mathrm{1}}{\mathrm{5}}\int_{\frac{\mathrm{5}\pi}{\mathrm{6}}} ^{\frac{\mathrm{5}\pi}{\mathrm{4}}} {sec}^{\mathrm{2}} {u}\:{du}\:=\frac{\mathrm{1}}{\mathrm{5}}\left[{tanu}\right]_{\frac{\mathrm{5}\pi}{\mathrm{6}}} ^{\frac{\mathrm{5}\pi}{\mathrm{4}}} =\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{5}\sqrt{\mathrm{3}}} \\ $$

Answered by Olaf last updated on 29/Nov/20

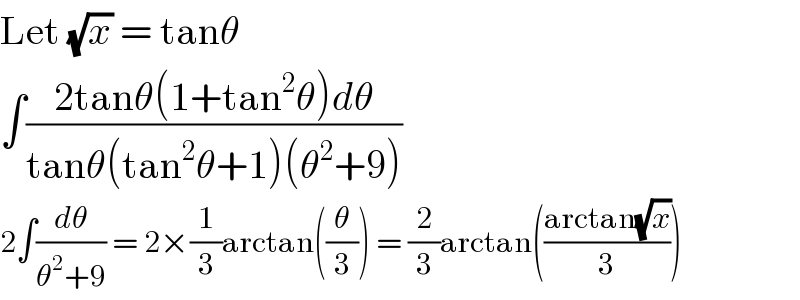
Let (√x) = tanθ ∫((2tanθ(1+tan^2 θ)dθ)/(tanθ(tan^2 θ+1)(θ^2 +9))) 2∫(dθ/(θ^2 +9)) = 2×(1/3)arctan((θ/3)) = (2/3)arctan(((arctan(√x))/3))

$$\mathrm{Let}\:\sqrt{{x}}\:=\:\mathrm{tan}\theta \\ $$$$\int\frac{\mathrm{2tan}\theta\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta\right){d}\theta}{\mathrm{tan}\theta\left(\mathrm{tan}^{\mathrm{2}} \theta+\mathrm{1}\right)\left(\theta^{\mathrm{2}} +\mathrm{9}\right)} \\ $$$$\mathrm{2}\int\frac{{d}\theta}{\theta^{\mathrm{2}} +\mathrm{9}}\:=\:\mathrm{2}×\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arctan}\left(\frac{\theta}{\mathrm{3}}\right)\:=\:\frac{\mathrm{2}}{\mathrm{3}}\mathrm{arctan}\left(\frac{\mathrm{arctan}\sqrt{{x}}}{\mathrm{3}}\right) \\ $$

Answered by liberty last updated on 29/Nov/20

letting z = tan^(−1) (√x) ⇒(√x) = tan z (dx/(2(√x))) = sec^2 z dz Y = ∫ ((2sec^2 z dz)/((tan^2 z+1)(z^2 +9))) Y= ∫ ((2 dz)/(z^2 +3^2 )) = (2/3) arctan ((z/3)) + c Y= (2/3)arctan (((tan^(−1) (√x) )/3)) + c

$${letting}\:{z}\:=\:\mathrm{tan}^{−\mathrm{1}} \sqrt{{x}}\:\Rightarrow\sqrt{{x}}\:=\:\mathrm{tan}\:{z} \\ $$$$\:\frac{{dx}}{\mathrm{2}\sqrt{{x}}}\:=\:\mathrm{sec}\:^{\mathrm{2}} {z}\:{dz}\: \\ $$$${Y}\:=\:\int\:\frac{\mathrm{2sec}\:^{\mathrm{2}} {z}\:{dz}}{\left(\mathrm{tan}\:^{\mathrm{2}} {z}+\mathrm{1}\right)\left({z}^{\mathrm{2}} +\mathrm{9}\right)}\: \\ $$$${Y}=\:\int\:\frac{\mathrm{2}\:{dz}}{{z}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} }\:=\:\frac{\mathrm{2}}{\mathrm{3}}\:\mathrm{arctan}\:\left(\frac{{z}}{\mathrm{3}}\right)\:+\:{c}\: \\ $$$${Y}=\:\frac{\mathrm{2}}{\mathrm{3}}\mathrm{arctan}\:\left(\frac{\mathrm{tan}^{−\mathrm{1}} \sqrt{{x}}\:}{\mathrm{3}}\right)\:+\:{c}\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com