Question Number 123937 by mnjuly1970 last updated on 29/Nov/20
$$\:\:\:\:\:\:\:\:\:\:\:\:...{nice}\:\:\:\:\:\:{calculus}... \\ $$$$\:{prove}\:{that}:: \\ $$$$\:\int_{\frac{−\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{4}}} \frac{\left(\pi−\mathrm{4}{x}\right){tan}\left({x}\right)}{\mathrm{1}−{tan}\left({x}\right)}{dx}\overset{???} {=}\pi{ln}\left(\mathrm{2}\right)−\frac{\pi^{\mathrm{2}} }{\mathrm{4}} \\ $$$$ \\ $$
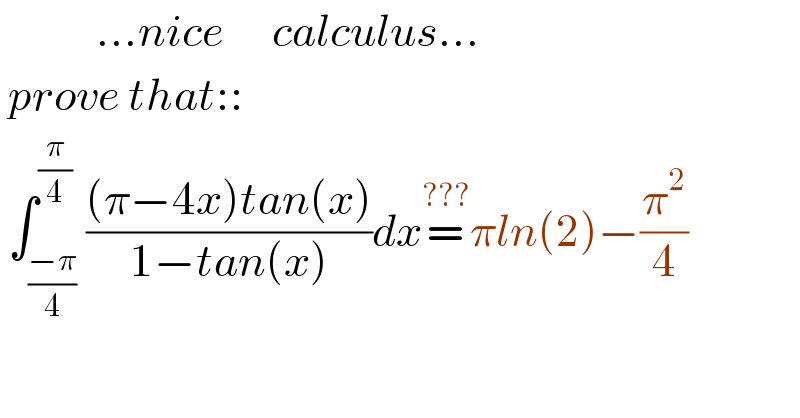
Answered by Dwaipayan Shikari last updated on 29/Nov/20
![∫_(−(π/4)) ^(π/4) (((π−4x)tanx)/(1−tanx))dx=4∫_(−(π/4)) ^(π/4) ((x(1−tanx))/(2tanx)) =4∫_0 ^(π/4) xcotx−x dx =2∫_0 ^(π/2) xcotx−x dx =2x[log(sinx)]_0 ^(π/2) −2∫_0 ^(π/2) log(sinx)−(π^2 /4) =−2.(−(π/2)log(2))−(π^2 /4) =πlog(2)−(π^2 /4) =−0.289815](Q123944.png)
$$\int_{−\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{4}}} \frac{\left(\pi−\mathrm{4}{x}\right){tanx}}{\mathrm{1}−{tanx}}{dx}=\mathrm{4}\int_{−\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{4}}} \frac{{x}\left(\mathrm{1}−{tanx}\right)}{\mathrm{2}{tanx}} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {xcotx}−{x}\:{dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {xcotx}−{x}\:{dx}\:=\mathrm{2}{x}\left[{log}\left({sinx}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} −\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left({sinx}\right)−\frac{\pi^{\mathrm{2}} }{\mathrm{4}} \\ $$$$=−\mathrm{2}.\left(−\frac{\pi}{\mathrm{2}}{log}\left(\mathrm{2}\right)\right)−\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\:=\pi{log}\left(\mathrm{2}\right)−\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\:\:=−\mathrm{0}.\mathrm{289815} \\ $$
Commented by mnjuly1970 last updated on 29/Nov/20
$${thank}\:{you}\:{so}\:{much}... \\ $$
Commented by CanovasCamiseros last updated on 29/Nov/20
$$\boldsymbol{{Please}}\:\boldsymbol{{who}}\:\boldsymbol{{can}}\:\boldsymbol{{help}}\:\boldsymbol{{me}}\:\boldsymbol{{with}}\:\boldsymbol{{hard}}\:\boldsymbol{{differential}}\:\boldsymbol{{equations}}\:\boldsymbol{{questions}}? \\ $$
Commented by Dwaipayan Shikari last updated on 29/Nov/20
$${Kindly}\:{post}\:{your}\:{problem}\:{sir}! \\ $$
Answered by mnjuly1970 last updated on 29/Nov/20
![solution:I=∫_((−π)/4) ^( (π/4)) (((π−4x)tan(x))/(1−tan(x)))dx note :: ∫_0 ^(π/2) ln(sin(x))dx=((−π)/2)ln(2) =^(u=(π/4)−x) 4∫_0 ^( (π/2)) ((xtan((π/4)−u))/(1−tan((π/4)−u)))du =4∫_0 ^( (π/2)) {((x((1−tan(u))/(1+tan(u))))/((2tan(x))/(1+tan(x))))}du =2∫_0 ^( (π/2)) xcot(x)(1−tan(x))dx =2∫_0 ^( (π/2)) xcot(x)dx−((π^2 /4)) =2{[xln(sin(x))]_0 ^(π/2) −∫_0 ^( (π/2)) ln(sin(x))dx}−(π^2 /4) =−2∫_0 ^( (π/2)) ln(sin(x))dx−(π^2 /4) =−2(((−π)/2)ln(2))−(π^2 /4)=πln(2)−(π^2 /4) ∴ ∫_((−π )/4) ^( (π/4)) (((π−4x)tan(x))/(1−tan(x)))dx=πln(2)−(π^2 /4) ✓](Q123940.png)
$${solution}:\mathrm{I}=\int_{\frac{−\pi}{\mathrm{4}}} ^{\:\frac{\pi}{\mathrm{4}}} \frac{\left(\pi−\mathrm{4}{x}\right){tan}\left({x}\right)}{\mathrm{1}−{tan}\left({x}\right)}{dx} \\ $$$${note}\:::\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({sin}\left({x}\right)\right){dx}=\frac{−\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\: \\ $$$$\:\:\:\:\:\overset{{u}=\frac{\pi}{\mathrm{4}}−{x}} {=}\mathrm{4}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \frac{{xtan}\left(\frac{\pi}{\mathrm{4}}−{u}\right)}{\mathrm{1}−{tan}\left(\frac{\pi}{\mathrm{4}}−{u}\right)}{du} \\ $$$$\:=\mathrm{4}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \left\{\frac{{x}\frac{\mathrm{1}−{tan}\left({u}\right)}{\mathrm{1}+{tan}\left({u}\right)}}{\frac{\mathrm{2}{tan}\left({x}\right)}{\mathrm{1}+{tan}\left({x}\right)}}\right\}{du} \\ $$$$\:=\mathrm{2}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {xcot}\left({x}\right)\left(\mathrm{1}−{tan}\left({x}\right)\right){dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {xcot}\left({x}\right){dx}−\left(\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\right) \\ $$$$\:\:=\mathrm{2}\left\{\left[{xln}\left({sin}\left({x}\right)\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} −\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {ln}\left({sin}\left({x}\right)\right){dx}\right\}−\frac{\pi^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\:\:\:=−\mathrm{2}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {ln}\left({sin}\left({x}\right)\right){dx}−\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\:\: \\ $$$$\:\:\:=−\mathrm{2}\left(\frac{−\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\right)−\frac{\pi^{\mathrm{2}} }{\mathrm{4}}=\pi{ln}\left(\mathrm{2}\right)−\frac{\pi^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\therefore\:\:\int_{\frac{−\pi\:\:}{\mathrm{4}}} ^{\:\frac{\pi}{\mathrm{4}}} \frac{\left(\pi−\mathrm{4}{x}\right){tan}\left({x}\right)}{\mathrm{1}−{tan}\left({x}\right)}{dx}=\pi{ln}\left(\mathrm{2}\right)−\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\:\:\checkmark \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\: \\ $$$$\: \\ $$