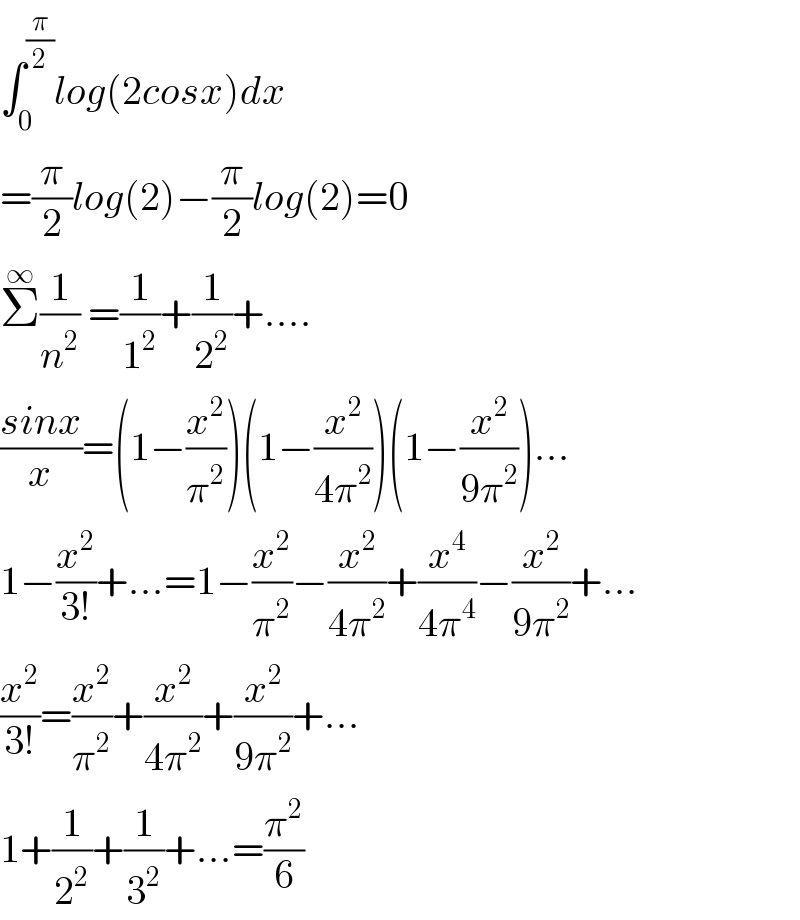Math Question and Answers


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 123977 by mnjuly1970 last updated on 29/Nov/20

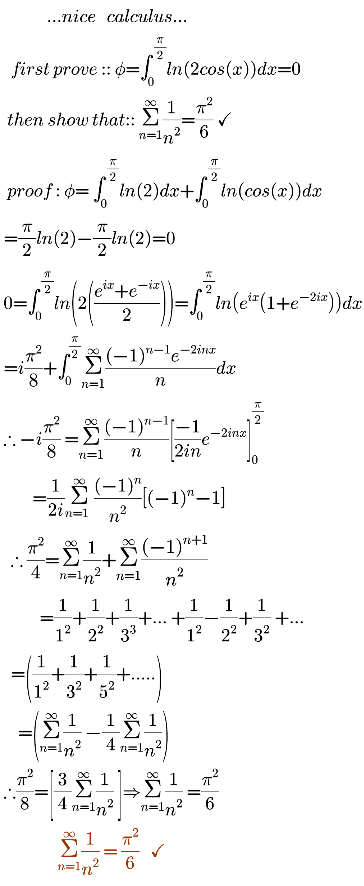
	Answered by mathmax by abdo last updated on 29/Nov/20
	$let A =∫_0 ^(π/2) ln(cosx)dx we have A =−(π/2)ln(2) also A =∫_0 ^(π/2) ln(((e^(ix) +e^(−ix) )/2))dx =∫_0 ^(π/2) ln(e^(ix) +e^(−ix) )dx−(π/2)ln(2) ⇒ ∫_0 ^(π/2) ln(e^(ix) +e^(−ix) )dx=0 ⇒∫_0 ^(π/2) ln(e^(ix) (1+e^(−2ix) ))=0 ⇒ [i(x^2 /2)]_0 ^(π/2) +∫_0 ^(π/2) ln(1+e^(−2ix) )dx we have ln^′ (1+u)=(1/(1+u))=Σ_(n=0) ^∞ (−1)^n u^n ⇒ln(1+u)=Σ_(n=0) ^∞ (((−1)^n u^(n+1) )/(n+1)) =Σ_(n=1) ^∞ (((−1)^(n−1) u^n )/n) ⇒ ∫_0 ^(π/2) ln(1+e^(−2ix) )=Σ_(n=1) ^∞ (((−1)^(n−1) )/n)∫_0 ^(π/2) e^(−2inx) dx =Σ_(n=1) ^∞ (((−1)^(n−1) )/n)×(1/(−2in))[e^(−2inx) ]_0 ^(π/2) =(i/2) Σ_(n=1) ^∞ (((−1)^(n−1) )/n^2 ){(−1)^n −1} =−iΣ_(n=0) ^∞ (1/((2n+1)^2 )) ⇒ i(π^2 /8)−iΣ_(n=0) ^∞ (1/((2n+1)^2 ))=0 ⇒Σ_(n=0) ^∞ (1/((2n+1)^2 ))=(π^2 /8) we have Σ_(n=1) ^∞ (1/n^2 )=Σ_(n=1) ^∞ (1/(4n^2 ))+Σ_(n=0) ^∞ (1/((2n+1)^2 )) ⇒ (3/4)Σ_(n=1) ^∞ (1/n^2 )=(π^2 /8) ⇒Σ_(n=1) ^∞ (1/n^2 )=(4/3)×(π^2 /8) =(π^2 /6)$
	$let A = \int_{0}^{\frac{π}{2}} \ln (cosx) dx we have A = - \frac{π}{2} \ln (2) also$ $A = \int_{0}^{\frac{π}{2}} \ln (\frac{e^{ix} + e^{- ix}}{2}) dx = \int_{0}^{\frac{π}{2}} \ln (e^{ix} + e^{- ix}) dx - \frac{π}{2} \ln (2) \Rightarrow$ $\int_{0}^{\frac{π}{2}} \ln (e^{ix} + e^{- ix}) dx = 0 \Rightarrow \int_{0}^{\frac{π}{2}} \ln (e^{ix} (1 + e^{- 2 ix})) = 0 \Rightarrow$ ${[i \frac{x^{2}}{2}]}_{0}^{\frac{π}{2}} + \int_{0}^{\frac{π}{2}} \ln (1 + e^{- 2 ix}) dx we have \ln^{^{'}} (1 + u) = \frac{1}{1 + u} = \sum_{n = 0}^{\infty} {(- 1)}^{n} u^{n}$ $\Rightarrow \ln (1 + u) = \sum_{n = 0}^{\infty} \frac{{(- 1)}^{n} u^{n + 1}}{n + 1} = \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1} u^{n}}{n} \Rightarrow$ $\int_{0}^{\frac{π}{2}} \ln (1 + e^{- 2 ix}) = \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1}}{n} \int_{0}^{\frac{π}{2}} e^{- 2 inx} dx$ $= \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1}}{n} \times \frac{1}{- 2 in} {[e^{- 2 inx}]}_{0}^{\frac{π}{2}}$ $= \frac{i}{2} \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1}}{n^{2}} {{(- 1)}^{n} - 1} = - i \sum_{n = 0}^{\infty} \frac{1}{{(2 n + 1)}^{2}} \Rightarrow$ $i \frac{π^{2}}{8} - i \sum_{n = 0}^{\infty} \frac{1}{{(2 n + 1)}^{2}} = 0 \Rightarrow \sum_{n = 0}^{\infty} \frac{1}{{(2 n + 1)}^{2}} = \frac{π^{2}}{8}$ $we have \sum_{n = 1}^{\infty} \frac{1}{n^{2}} = \sum_{n = 1}^{\infty} \frac{1}{{4 n}^{2}} + \sum_{n = 0}^{\infty} \frac{1}{{(2 n + 1)}^{2}} \Rightarrow$ $\frac{3}{4} \sum_{n = 1}^{\infty} \frac{1}{n^{2}} = \frac{π^{2}}{8} \Rightarrow \sum_{n = 1}^{\infty} \frac{1}{n^{2}} = \frac{4}{3} \times \frac{π^{2}}{8} = \frac{π^{2}}{6}$
	Commented by mnjuly1970 last updated on 29/Nov/20

	$t h a n k y o u s o m u c h s i r m a x$ $v e r y n i c e a s a l w a y s . . .$
	Commented by mathmax by abdo last updated on 30/Nov/20

	$you are welcome$
	Answered by Dwaipayan Shikari last updated on 30/Nov/20

	$\int_{0}^{\frac{π}{2}} l o g (2 c o s x) d x$ $= \frac{π}{2} l o g (2) - \frac{π}{2} l o g (2) = 0$ $\sum^{\infty} \frac{1}{n^{2}} = \frac{1}{1^{2}} + \frac{1}{2^{2}} + . . . .$ $\frac{s i n x}{x} = (1 - \frac{x^{2}}{π^{2}}) (1 - \frac{x^{2}}{4 π^{2}}) (1 - \frac{x^{2}}{9 π^{2}}) . . .$ $1 - \frac{x^{2}}{3!} + . . . = 1 - \frac{x^{2}}{π^{2}} - \frac{x^{2}}{4 π^{2}} + \frac{x^{4}}{4 π^{4}} - \frac{x^{2}}{9 π^{2}} + . . .$ $\frac{x^{2}}{3!} = \frac{x^{2}}{π^{2}} + \frac{x^{2}}{4 π^{2}} + \frac{x^{2}}{9 π^{2}} + . . .$ $1 + \frac{1}{2^{2}} + \frac{1}{3^{2}} + . . . = \frac{π^{2}}{6}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum