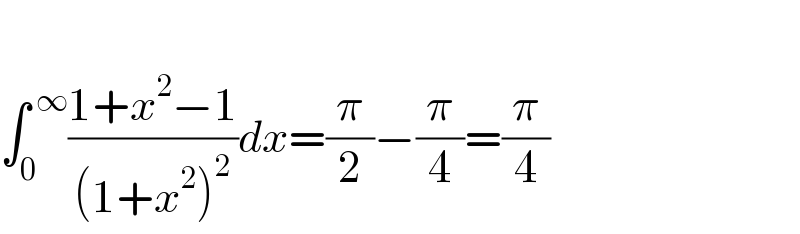Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 123998 by john_santu last updated on 30/Nov/20

$${\int }_0^{\mathrm{\infty }}\frac{x^2}{{(1+x^2)}^2}dx$$

Answered by liberty last updated on 30/Nov/20

$$substitutingx=\tan qwithupperlimit\frac{\pi }{2}$$$$andlowerlimit0$$$${\int }_0^{\pi /2}\frac{\tan {}^{2}q.\sec {}^{2}qdq}{\sec {}^{4}q}={\int }_0^{\pi /2}\sin {}^{2}qdq$$$$={\int }_0^{\pi /2}(\frac{1}{2}-\frac{1}{2}\cos 2q)dq={[\frac{1}{2}q-\frac{1}{4}\sin 2q]}_0^{\pi /2}$$$$=\frac{\pi }{4}.$$

Answered by Dwaipayan Shikari last updated on 30/Nov/20

$${\int }_0^{\mathrm{\infty }}\frac{x^2}{{(1+x^2)}^2}dx\frac{1}{1+x^2}=t\Rightarrow -\frac{2x}{{(1+x^2)}^2}=\frac{dt}{dx}x=\sqrt{\frac{1-t}{t}}$$$$=\frac{1}{2}{\int }_0^1\sqrt{\frac{1-t}{t}}dt=\frac{1}{2}{\int }_0^1{t}^{-\frac{1}{2}}{(1-t)}^{\frac{1}{2}}dt=\frac{1}{2}\beta (\frac{1}{2},\frac{3}{2})$$$$=\frac{{\mathrm{\Gamma }}^2\left(\frac{1}{2}\right)}{4}=\frac{\sqrt{\pi }.\sqrt{\pi }}{4}=\frac{\pi }{4}$$

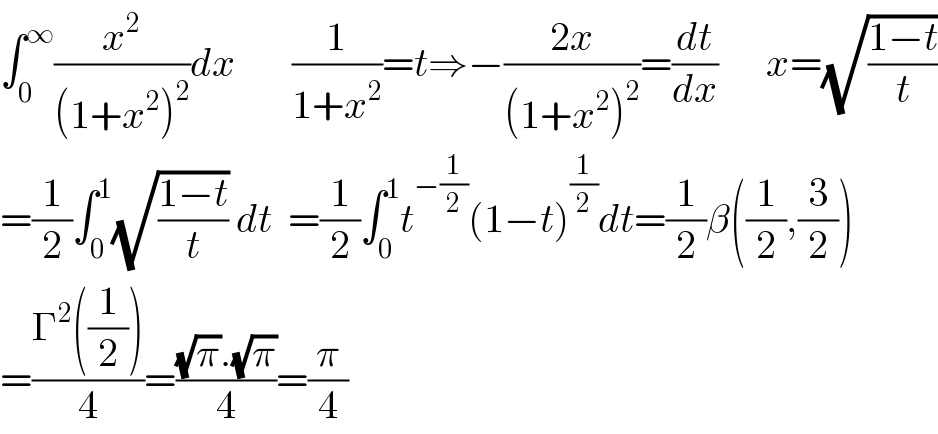
Answered by mathmax by abdo last updated on 30/Nov/20

$$\mathrm{I}={\int }_0^{\mathrm{\infty }}\frac{{\mathrm{x}}^2}{{({\mathrm{x}}^2+1)}^2}\mathrm{dx}\Rightarrow \mathrm{I}={\int }_0^{\mathrm{\infty }}\frac{{\mathrm{x}}^2+1-1}{{({\mathrm{x}}^2+1)}^2}\mathrm{dx}$$$$={\int }_0^{\mathrm{\infty }}\frac{\mathrm{dx}}{{\mathrm{x}}^2+1}-{\int }_0^{\mathrm{\infty }}\frac{\mathrm{dx}}{{({\mathrm{x}}^2+1)}^2}=\frac{\pi }{2}-\mathrm{J}\mathrm{with}\mathrm{J}={\int }_0^{\mathrm{\infty }}\frac{\mathrm{dx}}{{({\mathrm{x}}^2+1)}^2}$$$$2\mathrm{J}={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\frac{\mathrm{dx}}{{({\mathrm{x}}^2+1)}^2}\mathrm{let}\phi \left(\mathrm{z}\right)=\frac{1}{{({\mathrm{z}}^2+1)}^2}=\frac{1}{{(\mathrm{z}-\mathrm{i})}^2{(\mathrm{z}+\mathrm{i})}^2}$$$${\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\phi -\mathrm{z})\mathrm{dz}=2\mathrm{i}\pi \mathrm{Res}(\phi ,\mathrm{i})$$$$\mathrm{Res}(\phi ,\mathrm{i})={\lim }_{\mathrm{z}\to \mathrm{i}}\frac{1}{(2-1)!}{\left\{{(\mathrm{z}-\mathrm{i})}^2\phi \left(\mathrm{z}\right)\right\}}^{\left(1\right)}$$$$={\lim }_{\mathrm{z}\to \mathrm{i}}{\left\{{(\mathrm{z}+\mathrm{i})}^{-2}\right\}}^{\left(1\right)}={\lim }_{\mathrm{z}\to \mathrm{i}}-2{(\mathrm{z}+\mathrm{i})}^{-3}={\lim }_{\mathrm{z}\to \mathrm{i}}\frac{-2}{{(\mathrm{z}+\mathrm{i})}^3}$$$$=\frac{-2}{{\left(2\mathrm{i}\right)}^3}=\frac{-2}{-8\mathrm{i}}=\frac{1}{4\mathrm{i}}\Rightarrow {\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\phi \left(\mathrm{z}\right)\mathrm{dz}=2\mathrm{i}\pi \times \frac{1}{4\mathrm{i}}=\frac{\pi }{2}=2\mathrm{J}\Rightarrow$$$$\mathrm{J}=\frac{\pi }{4}\Rightarrow \mathrm{I}=\frac{\pi }{2}-\frac{\pi }{4}=\frac{\pi }{4}$$

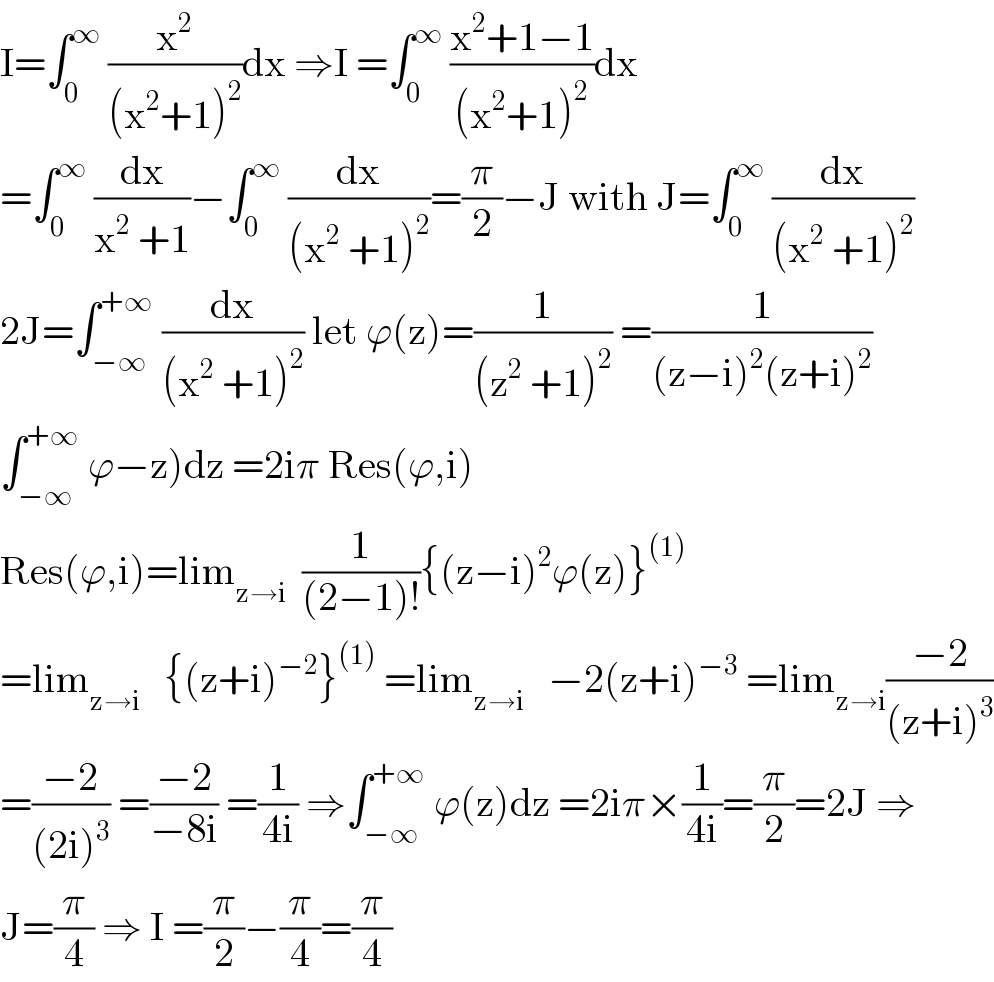
Answered by mnjuly1970 last updated on 01/Dec/20

$$$$$${\int }_0^{\mathrm{\infty }}\frac{1+x^2-1}{{(1+x^2)}^2}dx=\frac{\pi }{2}-\frac{\pi }{4}=\frac{\pi }{4}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com