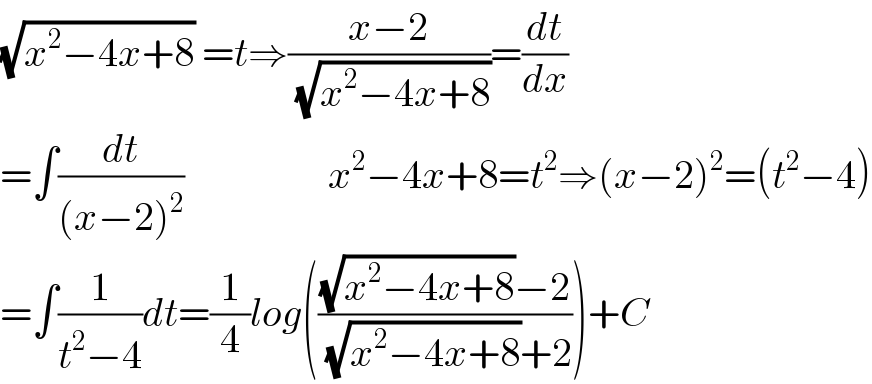Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 124000 by joki last updated on 30/Nov/20

Answered by liberty last updated on 30/Nov/20

$$\int \frac{dx}{(x-2)\sqrt{{(x-2)}^2+2^2}};[x-2=2\tan r]$$$$\mu \left(x\right)=\int \frac{2\sec {}^{2}rdr}{2\tan r\sqrt{4\sec {}^{2}r}}=\frac{1}{2}\int \frac{dr}{\sin r}$$$$\mu \left(x\right)=\frac{1}{2}\int \mathrm{cosec}rdr=\frac{1}{2}\ell n\mid \mathrm{cosec}r-\cot r\mid +c$$$$\mu \left(x\right)=\ell n\sqrt{\frac{\sqrt{x^2-4x+8}}{2}-\frac{2}{x-2}}+c$$

Answered by mathmax by abdo last updated on 30/Nov/20

$$\mathrm{A}=\int \frac{\mathrm{dx}}{(\mathrm{x}-2)\sqrt{{\mathrm{x}}^2-4\mathrm{x}+8}}\Rightarrow \mathrm{A}=\int \frac{\mathrm{dx}}{(\mathrm{x}-2)\sqrt{{(\mathrm{x}-2)}^2+4}}$$$$\mathrm{we}\mathrm{do}\mathrm{the}\mathrm{changement}\mathrm{x}-2=2\mathrm{sht}\Rightarrow$$$$\mathrm{A}=\int \frac{2\mathrm{cht}}{2\mathrm{sht}2\mathrm{cht}}\mathrm{dt}=\int \frac{\mathrm{dt}}{2\mathrm{sh}\left(\mathrm{t}\right)}=\int \frac{\mathrm{dt}}{{\mathrm{e}}^{\mathrm{t}}-{\mathrm{e}}^{-\mathrm{t}}}$$$${=}_{{\mathrm{e}}^{\mathrm{t}}=\mathrm{z}}\int \frac{\mathrm{dz}}{\mathrm{z}(\mathrm{z}-{\mathrm{z}}^{-1})}=\int \frac{\mathrm{dz}}{{\mathrm{z}}^2-1}=\frac{1}{2}\int (\frac{1}{\mathrm{z}-1}-\frac{1}{\mathrm{z}+1})\mathrm{dz}$$$$=\frac{1}{2}\ln \mid \frac{\mathrm{z}-1}{\mathrm{z}+1}\mid +\mathrm{k}\mathrm{we}\mathrm{have}\mathrm{t}=\mathrm{argsh}\left(\frac{\mathrm{x}-2}{2}\right)=\ln (\frac{\mathrm{x}-2}{2}+\sqrt{1+{\left(\frac{\mathrm{x}-2}{2}\right)}^2})$$$$\Rightarrow \mathrm{z}={\mathrm{e}}^{\mathrm{t}}=\frac{\mathrm{x}-2}{2}+\sqrt{1+{\left(\frac{\mathrm{x}-2}{2}\right)}^2}\Rightarrow$$$$\mathrm{A}=\frac{1}{2}\ln \mid \frac{\frac{\mathrm{x}-2}{2}+\frac{\sqrt{4+{(\mathrm{x}-2)}^2}}{2}-1\mid }{\frac{\mathrm{x}-2}{2}+\frac{\sqrt{4+{(\mathrm{x}-2)}^2}}{2}+1}\mid +\mathrm{k}$$$$=\frac{1}{2}\ln \mid \frac{\mathrm{x}-4+\sqrt{{(\mathrm{x}-2)}^2+4}}{\mathrm{x}+\sqrt{{(\mathrm{x}-2)}^2+4}}\mid +\mathrm{k}$$

Answered by Ar Brandon last updated on 30/Nov/20

$$\mathrm{t}=\frac{1}{\mathrm{x}-2}\Rightarrow \mathrm{dt}=-\frac{\mathrm{dx}}{{(\mathrm{x}-2)}^2}=-{\mathrm{t}}^2\mathrm{dx}$$$$\Rightarrow \mathcal{I}=-\int \frac{\mathrm{tdt}}{{\mathrm{t}}^2\sqrt{\frac{1}{{\mathrm{t}}^2}+4}}=-\int \frac{\mathrm{dt}}{\sqrt{1+{4\mathrm{t}}^2}}$$$$=-\frac{1}{2}\mathrm{Arcsinh}\left(2\mathrm{t}\right)+\mathcal{C}=-\frac{1}{2}\ln \mid 2\mathrm{t}+\sqrt{1+{4\mathrm{t}}^2}\mid +\mathcal{C}$$$$=-\frac{1}{2}\ln \mid \frac{2+\sqrt{{\mathrm{x}}^2-4\mathrm{x}+8}}{\mathrm{x}-2}\mid +\mathcal{C}$$

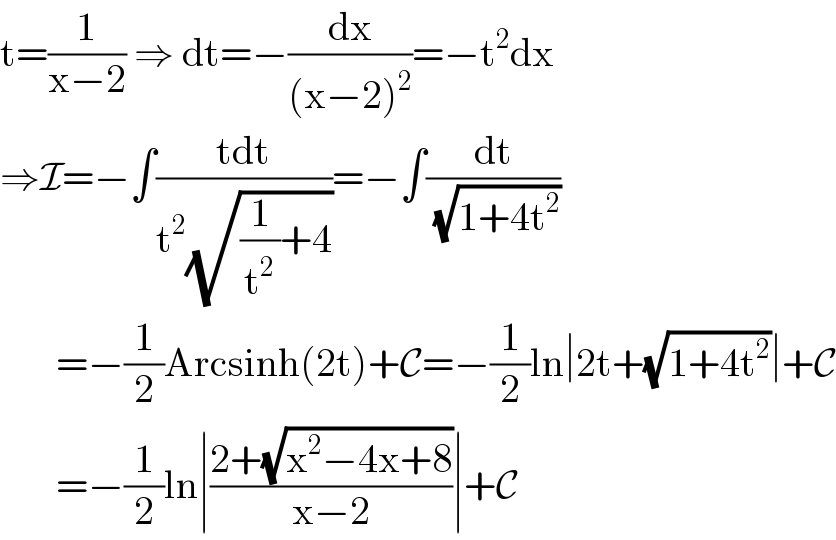
Commented by liberty last updated on 30/Nov/20

$$if2t=\cos u\Rightarrow I=-\int \frac{\frac{1}{2}(-\sin u)du}{\sqrt{1+\cos {}^{2}u}}$$$$howyougot\frac{1}{2}\mathrm{arc}\cos \left(2t\right)?$$

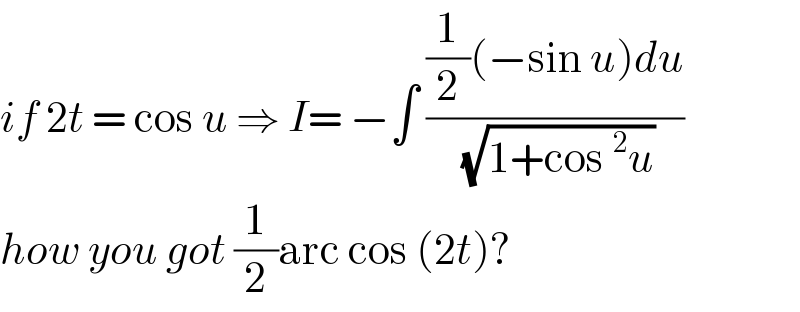
Commented by Ar Brandon last updated on 30/Nov/20

Found my mistake, thanks

Answered by MJS_new last updated on 30/Nov/20

$$\int \frac{dx}{(x-2)\sqrt{x^2-4x+8}}=$$$$[t=\frac{2+\sqrt{x^2-4x+8}}{x-2}\to dx=(-\frac{x^2}{2}+2x-4+\sqrt{x^2-4x+8})dt]$$$$=-\frac{1}{2}\int \frac{dt}{t}=-\frac{1}{2}\ln t=$$$$=-\frac{1}{2}\ln \mid \frac{2+\sqrt{x^2-4x+8}}{x-2}\mid +C$$

Answered by Dwaipayan Shikari last updated on 30/Nov/20

$$\sqrt{x^2-4x+8}=t\Rightarrow \frac{x-2}{\sqrt{x^2-4x+8}}=\frac{dt}{dx}$$$$=\int \frac{dt}{{(x-2)}^2}{x}^2-4x+8=t^2\Rightarrow {(x-2)}^2=(t^2-4)$$$$=\int \frac{1}{t^2-4}dt=\frac{1}{4}log\left(\frac{\sqrt{x^2-4x+8}-2}{\sqrt{x^2-4x+8}+2}\right)+C$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com