Math Question and Answers


Question and Answers Forum

All Questions Topic List
Geometry Questions
Previous in All Question Next in All Question
Previous in Geometry Next in Geometry
Question Number 124048 by ajfour last updated on 30/Nov/20

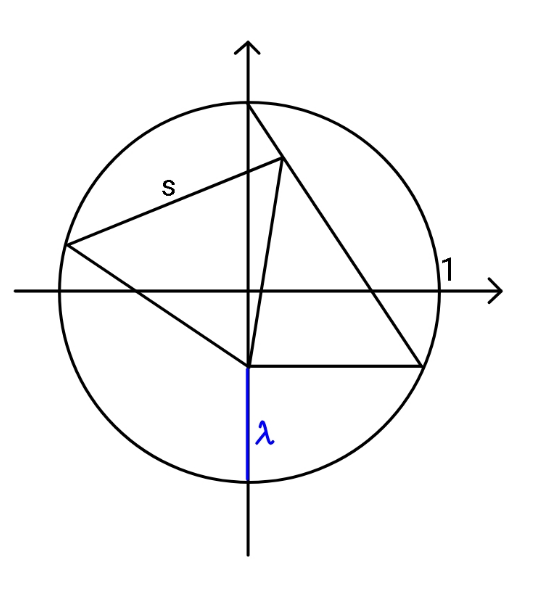
Commented by ajfour last updated on 30/Nov/20

$F i n d s i d e s o f e q u i l a t e r a l △ i n$ $t e r m s o f λ . R a d i u s i s u n i t y .$
	Answered by mr W last updated on 30/Nov/20

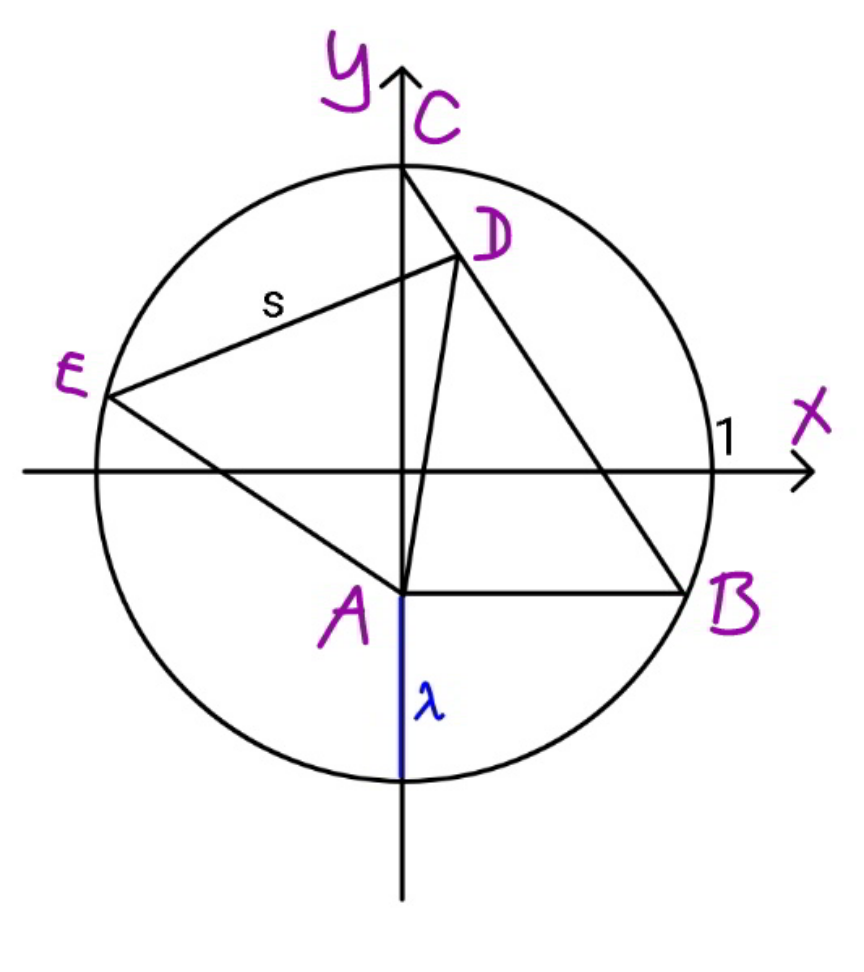
	Commented by ajfour last updated on 30/Nov/20
	$let B(h,−k) k = 1−λ h= (√(λ(2−λ))) eq. of BC y=1−(((2−λ)x)/( (√(λ(2−λ)))) = 1−(((1+k)x)/h) let D[t, 1−(((1+k)t)/h)] let F be midpoint of AD F [(t/2), ((1−k)/2)−(((1+k)t)/(2h))] AF = (t/2)+i[((1+k)/2)−(((1+k)t)/(2h))] FE=(((1+k)t)/(2h))−(((1+k))/2)+((it)/2) E[(((1+2k)t)/(2h))−(((1+k))/2), (t/2)+((1−k)/2)−(((1+k)t)/(2h))] E(−cos θ, sin θ) ⇒ {(((1+2k)t)/(2h))−(((1+k))/2)}^2 +{(t/2)+((1−k)/2)−(((1+k)t)/(2h))}^2 =1 ⇒ {(1+2k)t−h(1+k)}^2 + {h(1−k)−(1+k−h)t}^2 = 1 ⇒ {(1+2k)^2 −(1+k−h)^2 }t^2 +2{h(1−k)(1+k−h)−h(1+k)(1+2k)}t +h^2 [(1+k)^2 −(1−k)^2 ]−1=0 ⇒ (k^2 −h^2 +4k+2h+2hk)t^2 +2(h+hk−h^2 −hk−hk^2 +h^2 k −h−2hk−hk−2hk^2 )t +4kh^2 −1=0 ⇒ (k^2 +2hk−h^2 +4k+2h)t^2 −2(hk^2 −h^2 k+3hk+h^2 )t+4h^2 k−1 =0 ⇒ t=((hk(k−h)+h(3k+h))/(k(k+4)+h(2k−h+2))) −(√([((hk(k−h)+h(3k+h))/(k(k+4)+h(2k−h+2)))]^2 −(((4h^2 k−1))/(k(k+4)+h(2k−h+2))))) s = (√(t^2 +(1+k)^2 (h−t)^2 )) example: λ=0.6 k=0.4 , h=(√(0.6×1.4)) = (√(0.84)) t ≈ 0.11039604(✓) , 0.89381445(×) s ≈ 1.13395334$
	$l e t B (h, - k)$ $k = 1 - λ$ $h = \sqrt{λ (2 - λ)}$ $e q . o f B C$ $y = 1 - \frac{(2 - λ) x}{\sqrt{λ (2 - λ}} = 1 - \frac{(1 + k) x}{h}$ $l e t D [t, 1 - \frac{(1 + k) t}{h}]$ $l e t F b e m i d p o i n t o f A D$ $F [\frac{t}{2}, \frac{1 - k}{2} - \frac{(1 + k) t}{2 h}]$ $A F = \frac{t}{2} + i [\frac{1 + k}{2} - \frac{(1 + k) t}{2 h}]$ $F E = \frac{(1 + k) t}{2 h} - \frac{(1 + k)}{2} + \frac{i t}{2}$ $E [\frac{(1 + 2 k) t}{2 h} - \frac{(1 + k)}{2}, \frac{t}{2} + \frac{1 - k}{2} - \frac{(1 + k) t}{2 h}]$ $E (- \cos θ, \sin θ)$ $\Rightarrow$ ${\frac{(1 + 2 k) t}{2 h} - \frac{(1 + k)}{2}}^{2} + {\frac{t}{2} + \frac{1 - k}{2} - \frac{(1 + k) t}{2 h}}^{2} = 1$ $\Rightarrow$ ${(1 + 2 k) t - h (1 + k)}^{2} +$ ${h (1 - k) - (1 + k - h) t}^{2} = 1$ $\Rightarrow$ ${{(1 + 2 k)}^{2} - {(1 + k - h)}^{2}} t^{2}$ $+ 2 {h (1 - k) (1 + k - h) - h (1 + k) (1 + 2 k)} t$ $+ h^{2} [{(1 + k)}^{2} - {(1 - k)}^{2}] - 1 = 0$ $\Rightarrow$ $(k^{2} - h^{2} + 4 k + 2 h + 2 h k) t^{2}$ $+ 2 (h + h k - h^{2} - h k - {h k}^{2} + h^{2} k$ $- h - 2 h k - h k - 2 {h k}^{2}) t$ $+ 4 {k h}^{2} - 1 = 0$ $\Rightarrow$ $(k^{2} + 2 h k - h^{2} + 4 k + 2 h) t^{2}$ $- 2 ({h k}^{2} - h^{2} k + 3 h k + h^{2}) t + 4 h^{2} k - 1$ $= 0$ $\Rightarrow$ $t = \frac{h k (k - h) + h (3 k + h)}{k (k + 4) + h (2 k - h + 2)}$ $- \sqrt{{[\frac{h k (k - h) + h (3 k + h)}{k (k + 4) + h (2 k - h + 2)}]}^{2} - \frac{(4 h^{2} k - 1)}{k (k + 4) + h (2 k - h + 2)}}$ $s = \sqrt{t^{2} + {(1 + k)}^{2} {(h - t)}^{2}}$ $e x a m p l e : λ = 0.6$ $k = 0.4, h = \sqrt{0.6 \times 1.4} = \sqrt{0.84}$ $t \approx 0.11039604 (✓), 0.89381445 (\times)$ $s \approx 1.13395334$
	Commented by ajfour last updated on 01/Dec/20

	$w a i t i n g f o r Y o u r s o l u t i o n, m r W$ $S i r . .$
	Commented by mr W last updated on 01/Dec/20

	$i h a v e n o b e t t e r w a y f o r s o l v i n g .$ $i g u e s s s o l u t i o n e x i s t s o n l y f o r$ $s p e c i a l v a l u e s o f λ .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum