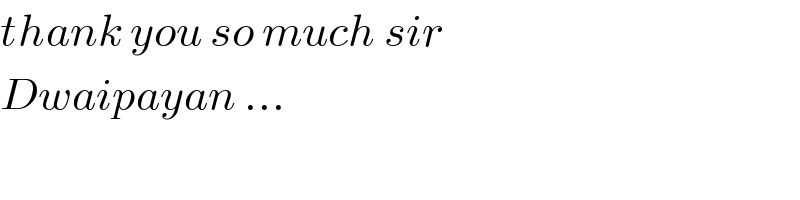Question Number 124178 by Dwaipayan Shikari last updated on 01/Dec/20
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\:\sqrt{{cos}^{\mathrm{4}} {x}+{sin}^{\mathrm{4}} {x}}}{dx} \\ $$
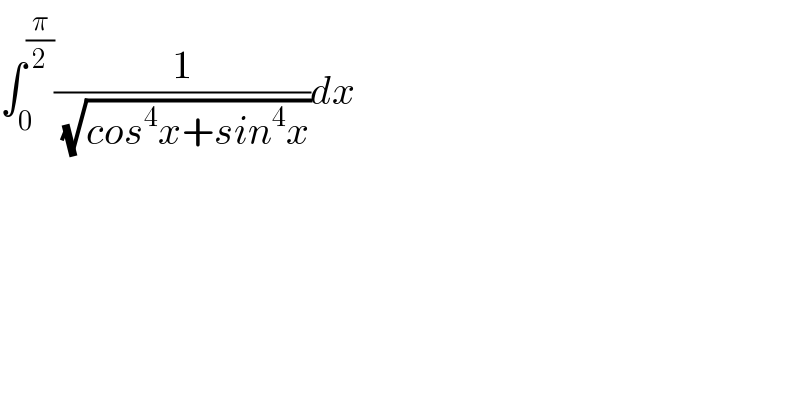
Commented by Dwaipayan Shikari last updated on 01/Dec/20
$${I}\:{have}\:{found}\:\frac{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)}{\mathrm{4}\sqrt{\pi}} \\ $$
Commented by MJS_new last updated on 01/Dec/20
$$\mathrm{me}\:\mathrm{too} \\ $$
Commented by Dwaipayan Shikari last updated on 01/Dec/20
https://brilliant.org/problems/another-apple-integral try this sir
Commented by MJS_new last updated on 01/Dec/20
![p, q >0 ∫_0 ^(π/2) (dx/( (√(pcos^4 x +qsin^4 x))))= [t=(q^(1/4) /p^(1/4) )tan x → dx=(p^(1/4) /q^(1/4) )cos^2 x dt] =(1/((pq)^(1/4) ))∫_0 ^(+∞) (dt/( (√(t^4 +1)))) and from here it′s easy](Q124188.png)
$${p},\:{q}\:>\mathrm{0} \\ $$$$\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{{dx}}{\:\sqrt{{p}\mathrm{cos}^{\mathrm{4}} \:{x}\:+{q}\mathrm{sin}^{\mathrm{4}} \:{x}}}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{{q}^{\mathrm{1}/\mathrm{4}} }{{p}^{\mathrm{1}/\mathrm{4}} }\mathrm{tan}\:{x}\:\rightarrow\:{dx}=\frac{{p}^{\mathrm{1}/\mathrm{4}} }{{q}^{\mathrm{1}/\mathrm{4}} }\mathrm{cos}^{\mathrm{2}} \:{x}\:{dt}\right] \\ $$$$=\frac{\mathrm{1}}{\left({pq}\right)^{\mathrm{1}/\mathrm{4}} }\underset{\mathrm{0}} {\overset{+\infty} {\int}}\frac{{dt}}{\:\sqrt{{t}^{\mathrm{4}} +\mathrm{1}}} \\ $$$$\mathrm{and}\:\mathrm{from}\:\mathrm{here}\:\mathrm{it}'\mathrm{s}\:\mathrm{easy} \\ $$
Commented by Dwaipayan Shikari last updated on 01/Dec/20
$${Do}\:{you}\:{have}\:{Brilliant}\:{app}\:,\:{sir}? \\ $$
Commented by MJS_new last updated on 01/Dec/20
$$\mathrm{no} \\ $$
Answered by mnjuly1970 last updated on 01/Dec/20
$$\:\:{I}=\underset{\mathrm{0}} {\int}^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}+{tan}^{\mathrm{2}} \left({x}\right)}{\:\sqrt{\mathrm{1}+{tan}^{\mathrm{4}} \left({x}\right)}}{dx} \\ $$$$\:\:\:\:\:\overset{{tan}\left({x}\right)={t}} {=}\int_{\mathrm{0}} ^{\infty} \frac{{dt}}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{4}} }} \\ $$$$\:\:\:\:\:\overset{{t}^{\mathrm{4}} ={y}} {=}\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\:\infty} \frac{{y}^{−\frac{\mathrm{3}}{\mathrm{4}}} }{\left(\mathrm{1}+{y}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{dy} \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\beta\left(\frac{\mathrm{1}}{\mathrm{4}},\frac{\mathrm{1}}{\mathrm{4}}\right)=\frac{\mathrm{1}}{\mathrm{4}}\:\frac{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)}{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\:\ast\frac{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)}{\:\sqrt{\pi}}\:\:\checkmark \\ $$$$\:\:\:\:\: \\ $$
Commented by Dwaipayan Shikari last updated on 01/Dec/20
$$\left.{Thanking}\:{for}\:{confirmation}\::\right) \\ $$
Commented by mnjuly1970 last updated on 01/Dec/20
$${thank}\:{you}\:{so}\:{much}\:{sir}\: \\ $$$${Dwaipayan}\:... \\ $$