Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 124201 by mnjuly1970 last updated on 01/Dec/20

$$:::nicecalculus:::$$$$pleaseprove:::$$$$\mathrm{\Omega }={\int }_0^{\mathrm{\infty }}\frac{x^{\frac{1}{2}}}{x^2+2x+5}dx=\frac{\pi }{\sqrt{\phi }}$$$$where\phi isGoldenratio...$$

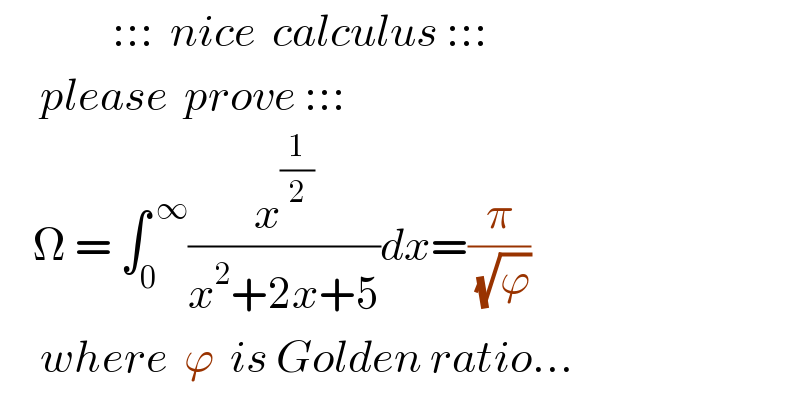
Answered by ajfour last updated on 02/Dec/20

$$I=\int \frac{\sqrt{x}dx}{{(x+1)}^2+{(2\phi -1)}^2}$$$$let\sqrt{x}=t\Rightarrow \sqrt{x}dx=2t^{2}dt$$$$I=\int \frac{2t^{2}dt}{{(t^2+1)}^2+{(2\phi -1)}^2}$$$$lett=\frac{1}{z}\Rightarrow dt=-\frac{dz}{z^2}$$$$I=\int \frac{2dz}{{(1+z^2)}^2+{(2\phi -1)}^2{z}^4}$$$$=\int \frac{2dz}{6z^4+2z^2+1}$$$$=\frac{1}{3}\int \frac{dz}{{(z^2+\frac{1}{6})}^2+{\left(\frac{\sqrt{5}}{6}\right)}^2}$$$$....$$

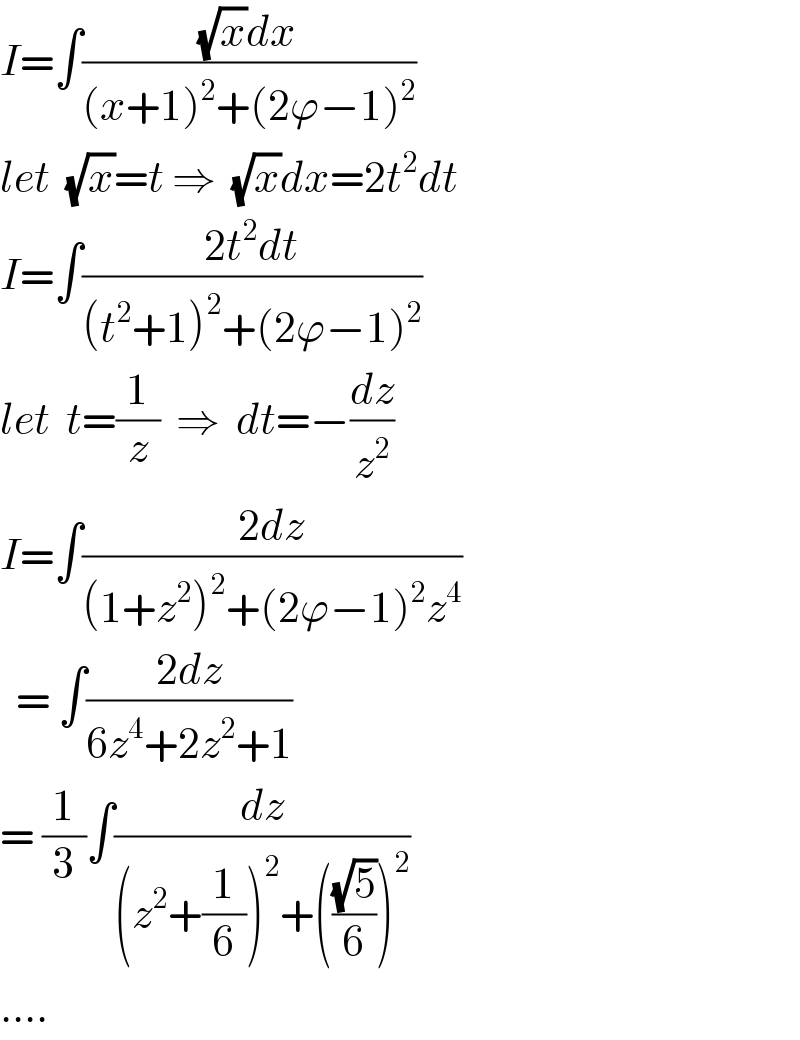
Commented by mindispower last updated on 02/Dec/20

$$sirajfouryourmethode$$$$worckssince6z^4+2z^2+1canbeefactorised$$$$inpolynomsofdegree2$$$$and\int \frac{dx}{x^2+ax+b}canbeesolved$$$$$$$$$$

Commented by mnjuly1970 last updated on 03/Dec/20

$$thankingforyoureffort$$$$sirajfor..$$

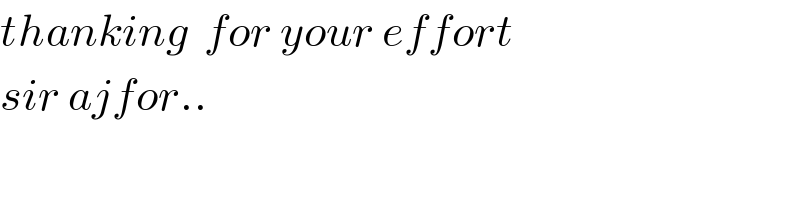
Commented by mnjuly1970 last updated on 03/Dec/20

Answered by mindispower last updated on 02/Dec/20

$$\mathrm{\Delta }={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\frac{z^{\frac{1}{2}}}{z^2+2z+5}dz={\int }_{-\mathrm{\infty }}^0\frac{z^{\frac{1}{2}}}{z^2+2z+5}dz+\mathrm{\Omega }$$$$=i{\int }_0^{\mathrm{\infty }}\frac{z^{\frac{1}{2}}}{z^2-2z+5}dz+\mathrm{\Omega }=\mathrm{\Omega }+it,\mathrm{\Omega },t\in \mathbb{R}$$$$\mathrm{\Delta }=2i\pi Res(\frac{z^{\frac{1}{2}}}{z^2+2z+5},z=-1+2i)$$$$.=2i\pi \frac{{(-1+2i)}^{\frac{1}{2}}}{2(-1+2i)+2}=\frac{\pi }{2}{(-1+2i)}^{\frac{1}{2}}$$$${(-1+2i)}^{\frac{1}{2}}=x+iy$$$$\Rightarrow xy=1,x^2+y^2=\sqrt{5},x^2-y^2=-1$$$$x={\left(\frac{\sqrt{5}-1}{2}\right)}^{\frac{1}{2}},y=\frac{2}{\sqrt{5}-1}={\left(\frac{\sqrt{5}+1}{2}\right)}^{\frac{1}{2}}$$$$x=\sqrt{\phi -1},y=\sqrt{\phi }$$$$\mathrm{\Delta }=\frac{\pi }{2}\sqrt{\phi -1}+\frac{\pi }{2}i\sqrt{\phi }$$$$\mathrm{\Omega }=Re\left(\mathrm{\Delta }\right)=\frac{\pi }{2}\sqrt{\phi -1}$$$${\phi }^2=\phi +1\Rightarrow \phi (\phi -1)=1$$$$\Rightarrow \sqrt{\phi -1}=\frac{1}{\sqrt{\phi }}$$$$\mathrm{\Omega }=\frac{\pi }{2}\sqrt{\phi -1}=\frac{\pi }{2\sqrt{\phi }}$$$$$$$$$$

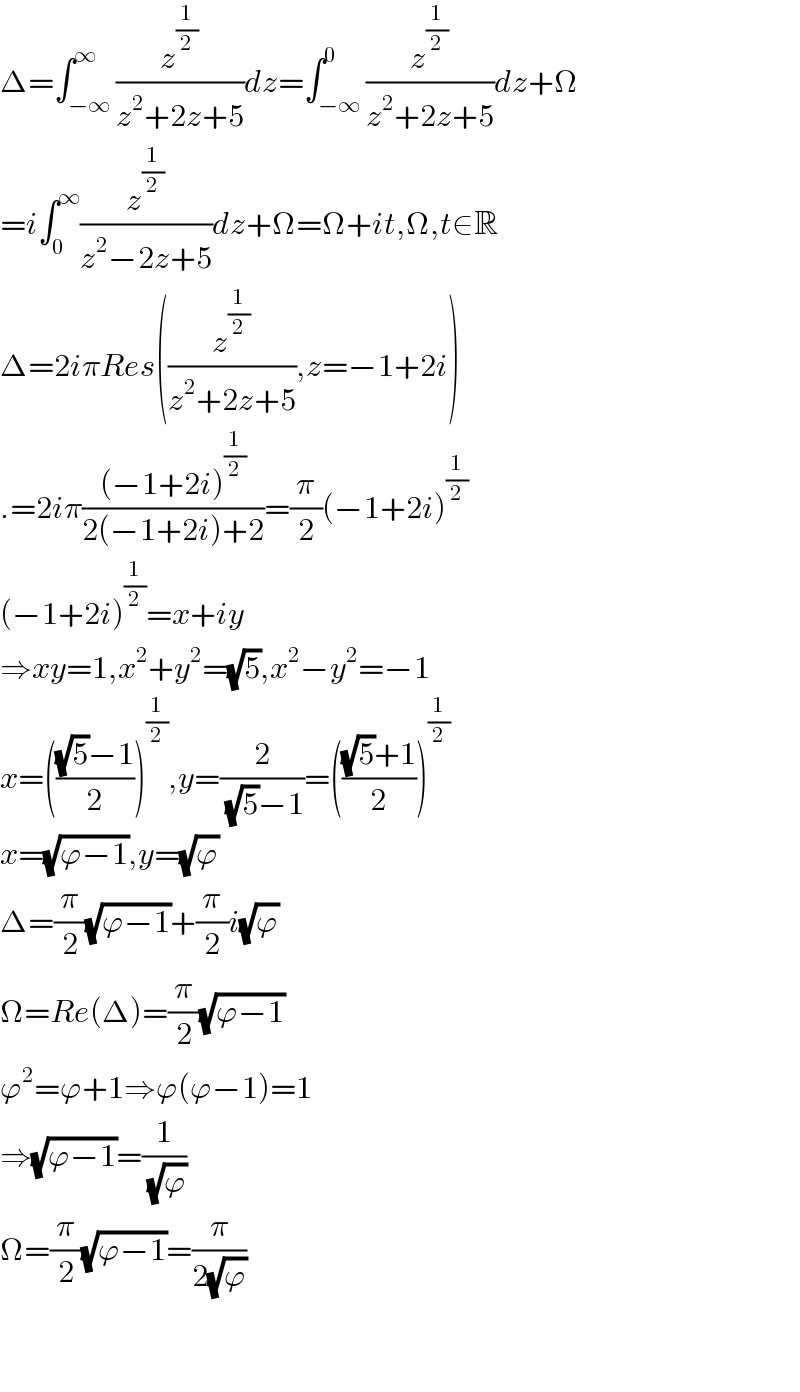
Commented by mnjuly1970 last updated on 02/Dec/20

$$excellent$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com