Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 12436 by tawa last updated on 22/Apr/17

∫ (dx/x^x ) dx

$$\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{x}} }\:\mathrm{dx} \\ $$

Commented by mrW1 last updated on 22/Apr/17

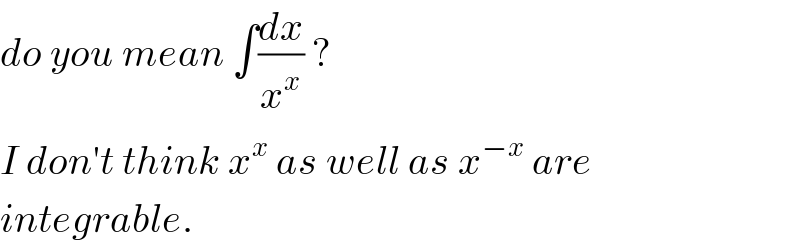
do you mean ∫(dx/x^x ) ? I don′t think x^x as well as x^(−x) are integrable.

$${do}\:{you}\:{mean}\:\int\frac{{dx}}{{x}^{{x}} }\:? \\ $$$${I}\:{don}'{t}\:{think}\:{x}^{{x}} \:{as}\:{well}\:{as}\:{x}^{−{x}} \:{are} \\ $$$${integrable}. \\ $$

Commented by tawa last updated on 22/Apr/17

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by FilupS last updated on 22/Apr/17

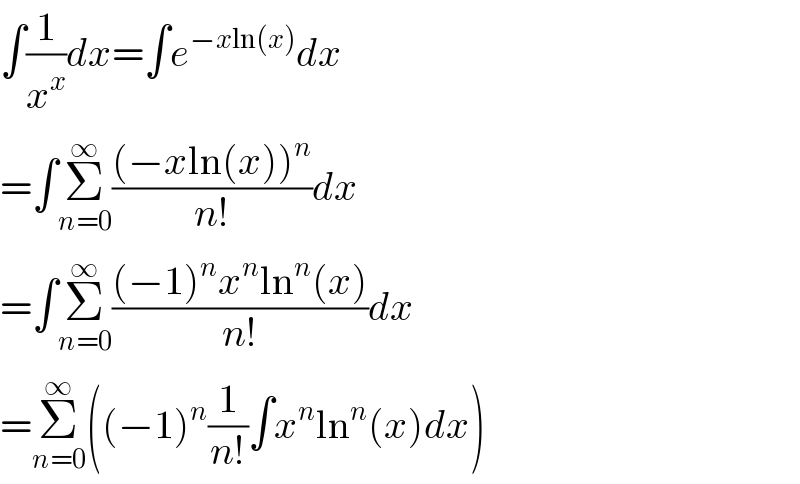
∫(1/x^x )dx=∫e^(−xln(x)) dx =∫Σ_(n=0) ^∞ (((−xln(x))^n )/(n!))dx =∫Σ_(n=0) ^∞ (((−1)^n x^n ln^n (x))/(n!))dx =Σ_(n=0) ^∞ ((−1)^n (1/(n!))∫x^n ln^n (x)dx)

$$\int\frac{\mathrm{1}}{{x}^{{x}} }{dx}=\int{e}^{−{x}\mathrm{ln}\left({x}\right)} {dx} \\ $$$$=\int\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−{x}\mathrm{ln}\left({x}\right)\right)^{{n}} }{{n}!}{dx} \\ $$$$=\int\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} {x}^{{n}} \mathrm{ln}^{{n}} \left({x}\right)}{{n}!}{dx} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\left(−\mathrm{1}\right)^{{n}} \frac{\mathrm{1}}{{n}!}\int{x}^{{n}} \mathrm{ln}^{{n}} \left({x}\right){dx}\right) \\ $$

Commented by FilupS last updated on 22/Apr/17

I can further solve if it were a definite integral ∫_0 ^( 1)

$$\mathrm{I}\:\mathrm{can}\:\mathrm{further}\:\mathrm{solve}\:\mathrm{if}\:\mathrm{it}\:\mathrm{were}\:\mathrm{a}\:\mathrm{definite} \\ $$$$\mathrm{integral}\:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \\ $$

Commented by FilupS last updated on 22/Apr/17

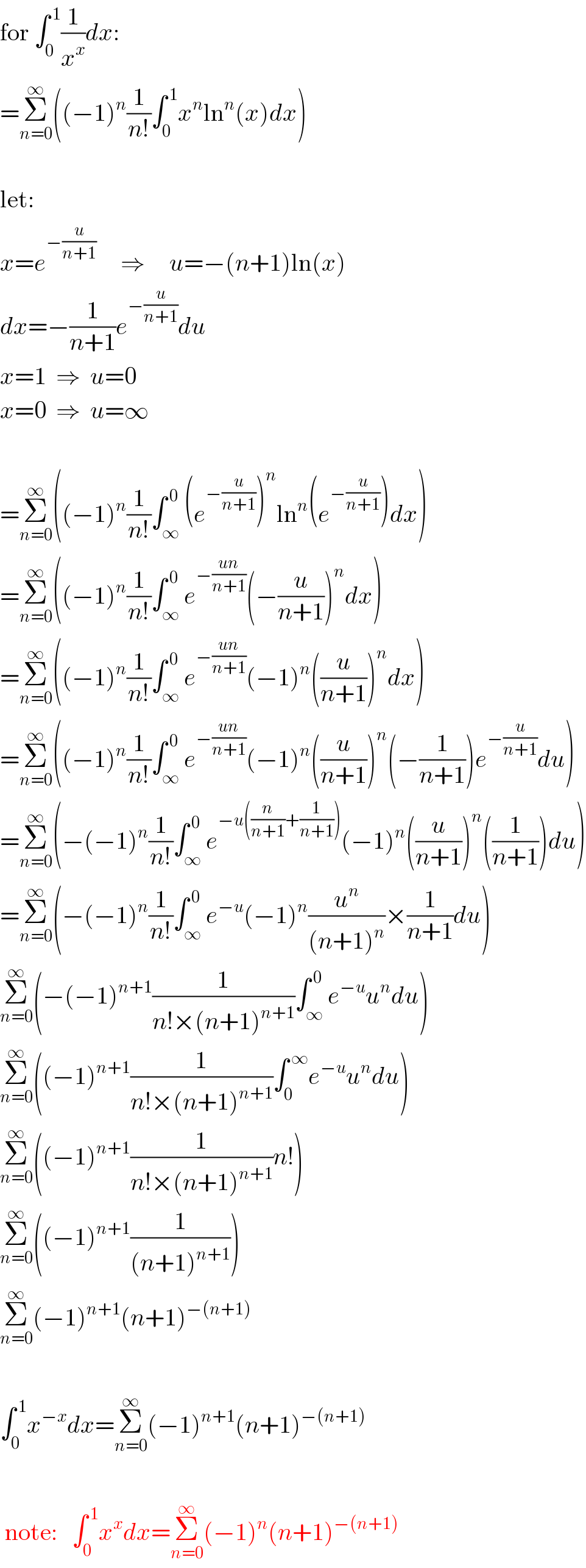
for ∫_0 ^( 1) (1/x^x )dx: =Σ_(n=0) ^∞ ((−1)^n (1/(n!))∫_0 ^( 1) x^n ln^n (x)dx) let: x=e^(−(u/(n+1))) ⇒ u=−(n+1)ln(x) dx=−(1/(n+1))e^(−(u/(n+1))) du x=1 ⇒ u=0 x=0 ⇒ u=∞ =Σ_(n=0) ^∞ ((−1)^n (1/(n!))∫_∞ ^( 0) (e^(−(u/(n+1))) )^n ln^n (e^(−(u/(n+1))) )dx) =Σ_(n=0) ^∞ ((−1)^n (1/(n!))∫_∞ ^( 0) e^(−((un)/(n+1))) (−(u/(n+1)))^n dx) =Σ_(n=0) ^∞ ((−1)^n (1/(n!))∫_∞ ^( 0) e^(−((un)/(n+1))) (−1)^n ((u/(n+1)))^n dx) =Σ_(n=0) ^∞ ((−1)^n (1/(n!))∫_∞ ^( 0) e^(−((un)/(n+1))) (−1)^n ((u/(n+1)))^n (−(1/(n+1)))e^(−(u/(n+1))) du) =Σ_(n=0) ^∞ (−(−1)^n (1/(n!))∫_∞ ^( 0) e^(−u((n/(n+1))+(1/(n+1)))) (−1)^n ((u/(n+1)))^n ((1/(n+1)))du) =Σ_(n=0) ^∞ (−(−1)^n (1/(n!))∫_∞ ^( 0) e^(−u) (−1)^n (u^n /((n+1)^n ))×(1/(n+1))du) Σ_(n=0) ^∞ (−(−1)^(n+1) (1/(n!×(n+1)^(n+1) ))∫_∞ ^( 0) e^(−u) u^n du) Σ_(n=0) ^∞ ((−1)^(n+1) (1/(n!×(n+1)^(n+1) ))∫_0 ^( ∞) e^(−u) u^n du) Σ_(n=0) ^∞ ((−1)^(n+1) (1/(n!×(n+1)^(n+1) ))n!) Σ_(n=0) ^∞ ((−1)^(n+1) (1/((n+1)^(n+1) ))) Σ_(n=0) ^∞ (−1)^(n+1) (n+1)^(−(n+1)) ∫_0 ^( 1) x^(−x) dx=Σ_(n=0) ^∞ (−1)^(n+1) (n+1)^(−(n+1)) note: ∫_0 ^( 1) x^x dx=Σ_(n=0) ^∞ (−1)^n (n+1)^(−(n+1))

$$\mathrm{for}\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}}{{x}^{{x}} }{dx}: \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\left(−\mathrm{1}\right)^{{n}} \frac{\mathrm{1}}{{n}!}\int_{\mathrm{0}} ^{\:\mathrm{1}} {x}^{{n}} \mathrm{ln}^{{n}} \left({x}\right){dx}\right) \\ $$$$\: \\ $$$$\mathrm{let}: \\ $$$${x}={e}^{−\frac{{u}}{{n}+\mathrm{1}}} \:\:\:\:\:\Rightarrow\:\:\:\:\:{u}=−\left({n}+\mathrm{1}\right)\mathrm{ln}\left({x}\right) \\ $$$${dx}=−\frac{\mathrm{1}}{{n}+\mathrm{1}}{e}^{−\frac{{u}}{{n}+\mathrm{1}}} {du} \\ $$$${x}=\mathrm{1}\:\:\Rightarrow\:\:{u}=\mathrm{0} \\ $$$${x}=\mathrm{0}\:\:\Rightarrow\:\:{u}=\infty \\ $$$$\: \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\left(−\mathrm{1}\right)^{{n}} \frac{\mathrm{1}}{{n}!}\int_{\infty} ^{\:\mathrm{0}} \left({e}^{−\frac{{u}}{{n}+\mathrm{1}}} \right)^{{n}} \mathrm{ln}^{{n}} \left({e}^{−\frac{{u}}{{n}+\mathrm{1}}} \right){dx}\right) \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\left(−\mathrm{1}\right)^{{n}} \frac{\mathrm{1}}{{n}!}\int_{\infty} ^{\:\mathrm{0}} {e}^{−\frac{{un}}{{n}+\mathrm{1}}} \left(−\frac{{u}}{{n}+\mathrm{1}}\right)^{{n}} {dx}\right) \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\left(−\mathrm{1}\right)^{{n}} \frac{\mathrm{1}}{{n}!}\int_{\infty} ^{\:\mathrm{0}} {e}^{−\frac{{un}}{{n}+\mathrm{1}}} \left(−\mathrm{1}\right)^{{n}} \left(\frac{{u}}{{n}+\mathrm{1}}\right)^{{n}} {dx}\right) \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\left(−\mathrm{1}\right)^{{n}} \frac{\mathrm{1}}{{n}!}\int_{\infty} ^{\:\mathrm{0}} {e}^{−\frac{{un}}{{n}+\mathrm{1}}} \left(−\mathrm{1}\right)^{{n}} \left(\frac{{u}}{{n}+\mathrm{1}}\right)^{{n}} \left(−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right){e}^{−\frac{{u}}{{n}+\mathrm{1}}} {du}\right) \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\left(−\mathrm{1}\right)^{{n}} \frac{\mathrm{1}}{{n}!}\int_{\infty} ^{\:\mathrm{0}} {e}^{−{u}\left(\frac{{n}}{{n}+\mathrm{1}}+\frac{\mathrm{1}}{{n}+\mathrm{1}}\right)} \left(−\mathrm{1}\right)^{{n}} \left(\frac{{u}}{{n}+\mathrm{1}}\right)^{{n}} \left(\frac{\mathrm{1}}{{n}+\mathrm{1}}\right){du}\right) \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\left(−\mathrm{1}\right)^{{n}} \frac{\mathrm{1}}{{n}!}\int_{\infty} ^{\:\mathrm{0}} {e}^{−{u}} \left(−\mathrm{1}\right)^{{n}} \frac{{u}^{{n}} }{\left({n}+\mathrm{1}\right)^{{n}} }×\frac{\mathrm{1}}{{n}+\mathrm{1}}{du}\right) \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \frac{\mathrm{1}}{{n}!×\left({n}+\mathrm{1}\right)^{{n}+\mathrm{1}} }\int_{\infty} ^{\:\mathrm{0}} {e}^{−{u}} {u}^{{n}} {du}\right) \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \frac{\mathrm{1}}{{n}!×\left({n}+\mathrm{1}\right)^{{n}+\mathrm{1}} }\int_{\mathrm{0}} ^{\:\infty} {e}^{−{u}} {u}^{{n}} {du}\right) \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \frac{\mathrm{1}}{{n}!×\left({n}+\mathrm{1}\right)^{{n}+\mathrm{1}} }{n}!\right) \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{{n}+\mathrm{1}} }\right) \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \left({n}+\mathrm{1}\right)^{−\left({n}+\mathrm{1}\right)} \\ $$$$\: \\ $$$$\int_{\mathrm{0}} ^{\:\mathrm{1}} {x}^{−{x}} {dx}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \left({n}+\mathrm{1}\right)^{−\left({n}+\mathrm{1}\right)} \\ $$$$\: \\ $$$$\:\mathrm{note}:\:\:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} {x}^{{x}} {dx}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \left({n}+\mathrm{1}\right)^{−\left({n}+\mathrm{1}\right)} \\ $$

Commented by tawa last updated on 23/Apr/17

Wow God bless you sir.

$$\mathrm{Wow}\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com