Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 124566 by bemath last updated on 04/Dec/20

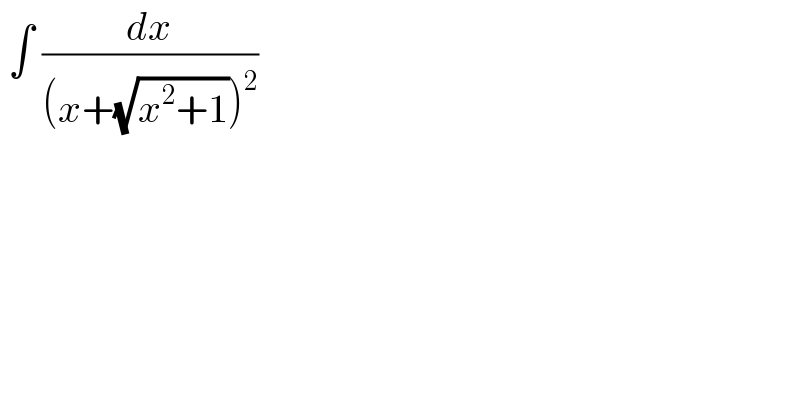
∫ (dx/((x+(√(x^2 +1)))^2 ))

$$\:\int\:\frac{{dx}}{\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} }\: \\ $$

Answered by liberty last updated on 05/Dec/20

∫ (dx/((x+(√(x^2 +1)))^2 )) = ? (1/(x+(√(x^2 +1)))) = ((x−(√(x^2 +1)))/(x^2 −(x^2 +1))) = (√(x^2 +1)) −x ∫ (dx/((x+(√(x^2 +1)))^2 )) = ∫((√(x^2 +1)) −x)^2 dx ∫ 2x^2 +1−2x(√(x^2 +1)) dx = (2/3)x^3 +x−(2/3)(x^2 +1)(√(x^2 +1)) + c =(2/3)(x^2 +1)[x−(√(x^2 +1)) ] + c = (2/3)(x^2 +1)[ ((−1)/(x+(√(x^2 +1)))) ] + c = −((2(x^2 +1))/(3(x+(√(x^2 +1))))) + c If ∫_0 ^( ∞) (dx/((x+(√(x^2 +1)))^2 )) = lim_(p→∞) −(2/3)[((x^2 +1)/(x+(√(x^2 +1)))) ]_0 ^p = −(2/3)[ lim_(p→∞) ((x^2 +1)/(x+(√(x^2 +1)))) −1 ] = −(2/3) [0−1] = (2/3)

$$\:\int\:\frac{{dx}}{\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} }\:=\:? \\ $$$$\frac{\mathrm{1}}{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}\:=\:\frac{{x}−\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{{x}^{\mathrm{2}} −\left({x}^{\mathrm{2}} +\mathrm{1}\right)}\:=\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:−{x} \\ $$$$\int\:\frac{{dx}}{\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} }\:=\:\int\left(\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:−{x}\right)^{\mathrm{2}} \:{dx}\: \\ $$$$\int\:\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}{x}\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:{dx}\:=\:\frac{\mathrm{2}}{\mathrm{3}}{x}^{\mathrm{3}} +{x}−\frac{\mathrm{2}}{\mathrm{3}}\left({x}^{\mathrm{2}} +\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:+\:{c} \\ $$$$\:=\frac{\mathrm{2}}{\mathrm{3}}\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left[{x}−\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:\right]\:+\:{c}\: \\ $$$$\:=\:\frac{\mathrm{2}}{\mathrm{3}}\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left[\:\frac{−\mathrm{1}}{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}\:\right]\:+\:{c}\: \\ $$$$\:=\:−\frac{\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{3}\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)}\:+\:{c}\: \\ $$$${If}\:\underset{\mathrm{0}} {\overset{\:\infty} {\int}}\:\frac{{dx}}{\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} }\:=\:\underset{{p}\rightarrow\infty} {\mathrm{lim}}\:−\frac{\mathrm{2}}{\mathrm{3}}\left[\frac{{x}^{\mathrm{2}} +\mathrm{1}}{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}\:\right]_{\mathrm{0}} ^{{p}} \\ $$$$\:=\:−\frac{\mathrm{2}}{\mathrm{3}}\left[\:\underset{{p}\rightarrow\infty} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} +\mathrm{1}}{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}\:−\mathrm{1}\:\right]\:=\:−\frac{\mathrm{2}}{\mathrm{3}}\:\left[\mathrm{0}−\mathrm{1}\right] \\ $$$$\:=\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$

Answered by Dwaipayan Shikari last updated on 04/Dec/20

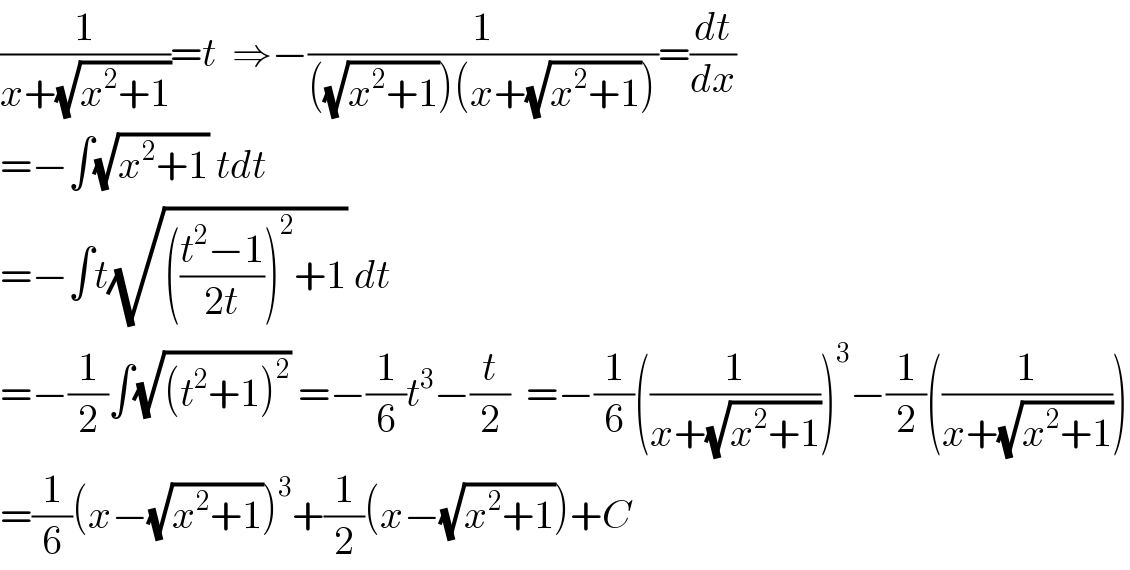
(1/(x+(√(x^2 +1))))=t ⇒−(1/(((√(x^2 +1)))(x+(√(x^2 +1)))))=(dt/dx) =−∫(√(x^2 +1)) tdt =−∫t(√((((t^2 −1)/(2t)))^2 +1)) dt =−(1/2)∫(√((t^2 +1)^2 )) =−(1/6)t^3 −(t/2) =−(1/6)((1/(x+(√(x^2 +1)))))^3 −(1/2)((1/(x+(√(x^2 +1))))) =(1/6)(x−(√(x^2 +1)))^3 +(1/2)(x−(√(x^2 +1)))+C

$$\frac{\mathrm{1}}{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}={t}\:\:\Rightarrow−\frac{\mathrm{1}}{\left(\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)}=\frac{{dt}}{{dx}} \\ $$$$=−\int\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:{tdt}\:\:\: \\ $$$$=−\int{t}\sqrt{\left(\frac{{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{t}}\right)^{\mathrm{2}} +\mathrm{1}}\:{dt} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int\sqrt{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:=−\frac{\mathrm{1}}{\mathrm{6}}{t}^{\mathrm{3}} −\frac{{t}}{\mathrm{2}}\:\:=−\frac{\mathrm{1}}{\mathrm{6}}\left(\frac{\mathrm{1}}{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}\right)^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\left({x}−\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{2}}\left({x}−\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)+{C} \\ $$

Answered by Ar Brandon last updated on 04/Dec/20

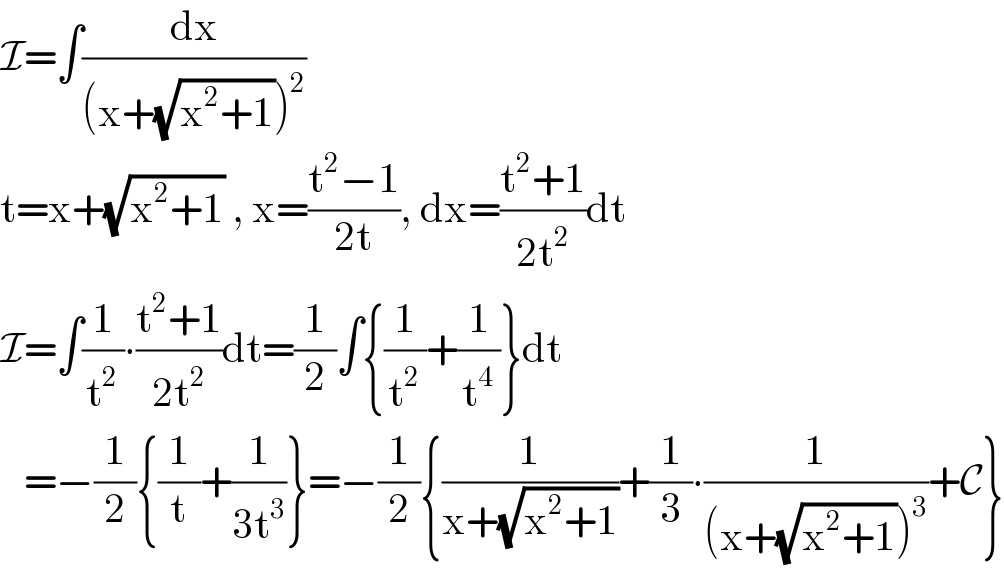
I=∫(dx/((x+(√(x^2 +1)))^2 )) t=x+(√(x^2 +1)) , x=((t^2 −1)/(2t)), dx=((t^2 +1)/(2t^2 ))dt I=∫(1/t^2 )∙((t^2 +1)/(2t^2 ))dt=(1/2)∫{(1/t^2 )+(1/t^4 )}dt =−(1/2){(1/t)+(1/(3t^3 ))}=−(1/2){(1/(x+(√(x^2 +1))))+(1/3)∙(1/((x+(√(x^2 +1)))^3 ))+C}

$$\mathcal{I}=\int\frac{\mathrm{dx}}{\left(\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} } \\ $$$$\mathrm{t}=\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\:,\:\mathrm{x}=\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2t}},\:\mathrm{dx}=\frac{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$\mathcal{I}=\int\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\centerdot\frac{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2t}^{\mathrm{2}} }\mathrm{dt}=\frac{\mathrm{1}}{\mathrm{2}}\int\left\{\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{4}} }\right\}\mathrm{dt} \\ $$$$\:\:\:=−\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\mathrm{1}}{\mathrm{t}}+\frac{\mathrm{1}}{\mathrm{3t}^{\mathrm{3}} }\right\}=−\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\mathrm{1}}{\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}}+\frac{\mathrm{1}}{\mathrm{3}}\centerdot\frac{\mathrm{1}}{\left(\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{3}} }+\mathcal{C}\right\} \\ $$

Answered by Ar Brandon last updated on 04/Dec/20

I=∫(dx/((x+(√(x^2 +1)))^2 )) x=tanθ ⇒ dx=sec^2 θdθ I=∫((sec^2 θdθ)/((tanθ+(√(tan^2 θ+1)))^2 ))=∫((sec^2 θdθ)/((tanθ+secθ)^2 )) =∫(dθ/((sinθ+1)^2 ))=∫(((1−sinθ)^2 )/((1−sin^2 θ)^2 ))dθ =∫{((1−2sinθ+sin^2 θ)/(cos^4 θ))}dθ=∫{((cos^2 θ−2sinθ+2sin^2 θ)/(cos^4 θ))}dθ =∫sec^2 θdθ+2∫(((−sinθ))/(cos^4 θ))dθ+2∫tan^2 θsec^2 θdθ =tanθ−(2/(3cos^3 θ))+((2tan^3 θ)/3)+C where θ=tan^(−1) (x)

$$\mathcal{I}=\int\frac{\mathrm{dx}}{\left(\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} } \\ $$$$\mathrm{x}=\mathrm{tan}\theta\:\Rightarrow\:\mathrm{dx}=\mathrm{sec}^{\mathrm{2}} \theta\mathrm{d}\theta \\ $$$$\mathcal{I}=\int\frac{\mathrm{sec}^{\mathrm{2}} \theta\mathrm{d}\theta}{\left(\mathrm{tan}\theta+\sqrt{\mathrm{tan}^{\mathrm{2}} \theta+\mathrm{1}}\right)^{\mathrm{2}} }=\int\frac{\mathrm{sec}^{\mathrm{2}} \theta\mathrm{d}\theta}{\left(\mathrm{tan}\theta+\mathrm{sec}\theta\right)^{\mathrm{2}} } \\ $$$$\:\:\:=\int\frac{\mathrm{d}\theta}{\left(\mathrm{sin}\theta+\mathrm{1}\right)^{\mathrm{2}} }=\int\frac{\left(\mathrm{1}−\mathrm{sin}\theta\right)^{\mathrm{2}} }{\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \theta\right)^{\mathrm{2}} }\mathrm{d}\theta \\ $$$$\:\:\:=\int\left\{\frac{\mathrm{1}−\mathrm{2sin}\theta+\mathrm{sin}^{\mathrm{2}} \theta}{\mathrm{cos}^{\mathrm{4}} \theta}\right\}\mathrm{d}\theta=\int\left\{\frac{\mathrm{cos}^{\mathrm{2}} \theta−\mathrm{2sin}\theta+\mathrm{2sin}^{\mathrm{2}} \theta}{\mathrm{cos}^{\mathrm{4}} \theta}\right\}\mathrm{d}\theta \\ $$$$\:\:\:=\int\mathrm{sec}^{\mathrm{2}} \theta\mathrm{d}\theta+\mathrm{2}\int\frac{\left(−\mathrm{sin}\theta\right)}{\mathrm{cos}^{\mathrm{4}} \theta}\mathrm{d}\theta+\mathrm{2}\int\mathrm{tan}^{\mathrm{2}} \theta\mathrm{sec}^{\mathrm{2}} \theta\mathrm{d}\theta \\ $$$$\:\:\:=\mathrm{tan}\theta−\frac{\mathrm{2}}{\mathrm{3cos}^{\mathrm{3}} \theta}+\frac{\mathrm{2tan}^{\mathrm{3}} \theta}{\mathrm{3}}+\mathcal{C} \\ $$$${where}\:\theta=\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com