
Question and Answers Forum
Question Number 124594 by physicstutes last updated on 04/Dec/20
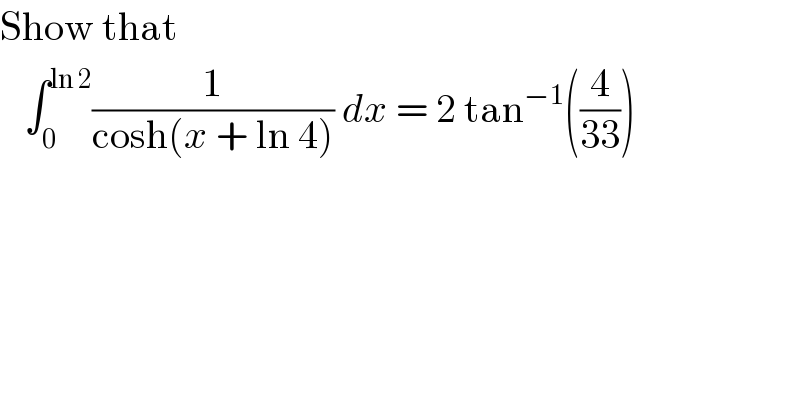
Commented by mohammad17 last updated on 04/Dec/20
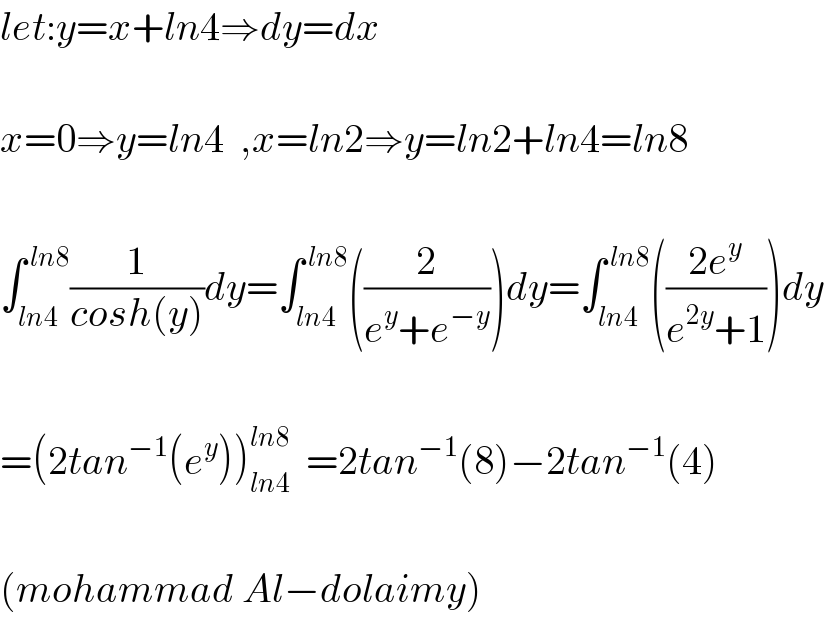
Answered by Ar Brandon last updated on 04/Dec/20
![I=∫_0 ^(ln2) (1/(cosh(x+ln4)))dx x+ln4=u ⇒ dx=du I=∫_(ln4) ^(ln8) (du/(cosh(u)))=∫_(ln4) ^(ln8) (du/((1/2)(e^u +e^(−u) ))) =2∫_(ln4) ^(ln8) ((e^u du)/(e^(2u) +1))=2∫_4 ^8 (dt/(t^2 +1))=2[tan^(−1) (t)]_4 ^8 =2[tan^(−1) (8)−tan^(−1) (4)]](Q124604.png)
| ||
Question and Answers Forum | ||
Question Number 124594 by physicstutes last updated on 04/Dec/20 | ||
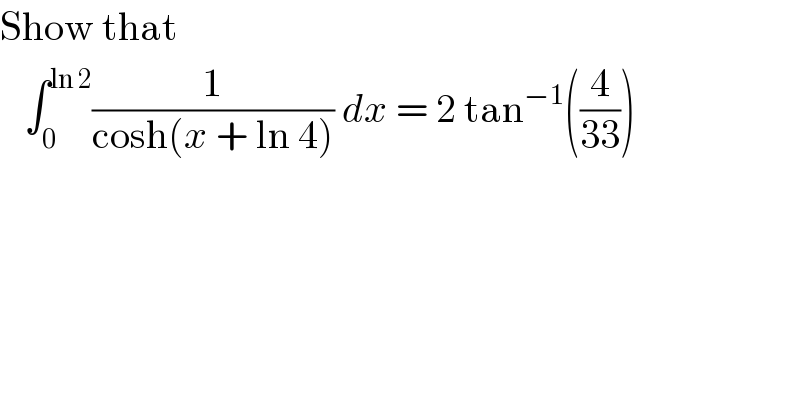 | ||
Commented by mohammad17 last updated on 04/Dec/20 | ||
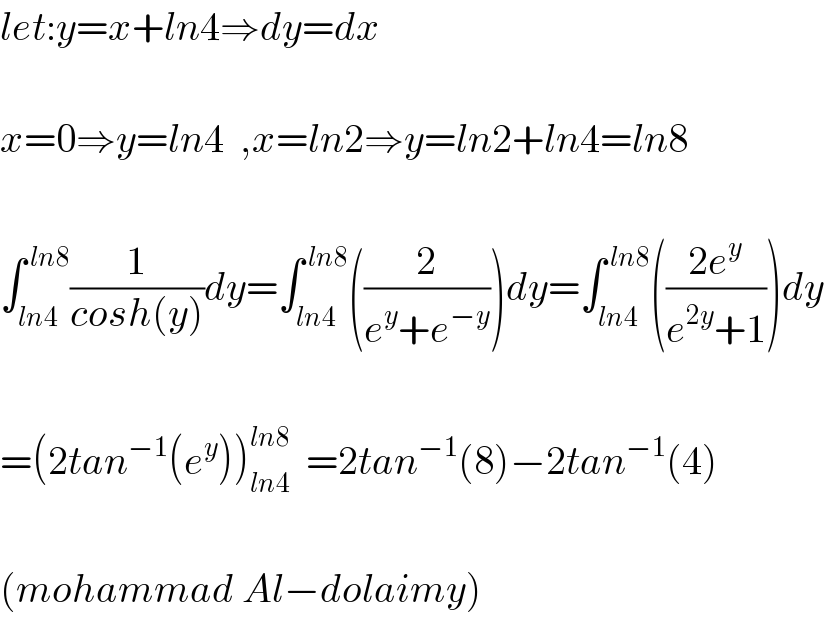 | ||
Answered by Ar Brandon last updated on 04/Dec/20 | ||
![I=∫_0 ^(ln2) (1/(cosh(x+ln4)))dx x+ln4=u ⇒ dx=du I=∫_(ln4) ^(ln8) (du/(cosh(u)))=∫_(ln4) ^(ln8) (du/((1/2)(e^u +e^(−u) ))) =2∫_(ln4) ^(ln8) ((e^u du)/(e^(2u) +1))=2∫_4 ^8 (dt/(t^2 +1))=2[tan^(−1) (t)]_4 ^8 =2[tan^(−1) (8)−tan^(−1) (4)]](Q124604.png) | ||
| ||