
Question and Answers Forum
Question Number 124632 by liberty last updated on 05/Dec/20
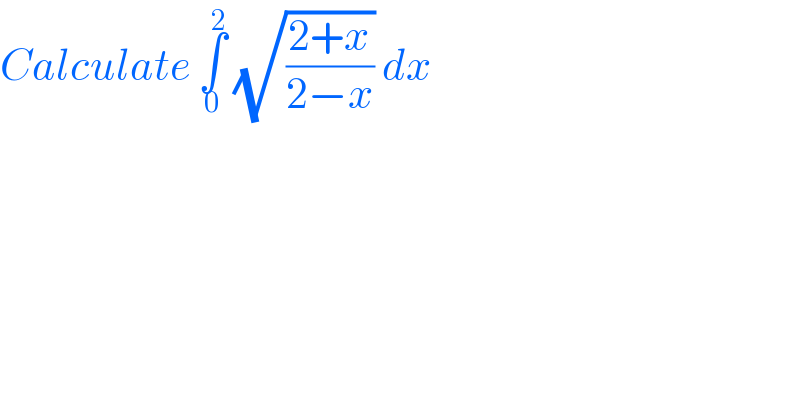
Answered by bemath last updated on 05/Dec/20
![put x=2cos 2θ I=∫_(π/4) ^0 (√((2+2cos 2θ)/(2−2cos 2θ))) (−4sin 2θ) dθ I= 4∫_0 ^(π/4) (√((1+cos 2θ)/(1−cos 2θ))) (2sin θ cos θ)dθ I= 4∫_0 ^(π/4) 2cos^2 θ dθ I=4 [ ((sin 2θ)/2) + θ ]_( 0) ^(π/4) = 4((1/2)+(π/4)) I=2+π](Q124633.png)
Answered by mathmax by abdo last updated on 05/Dec/20
![A =∫_0 ^2 (√((2+x)/(2−x)))dx we do the changement x=2cost ⇒ A =∫_(π/2) ^0 (√((1+cost)/(1−cost)))(−2sint)dt =2∫_0 ^(π/2) ((cos((t/2)))/(sin((t/2))))×2cos((t/2))sin((t/2))dt =4 ∫_0 ^(π/2) cos^2 ((t/2))dt =4∫_0 ^(π/2) ((1+cost)/2)dt =2∫_0 ^(π/2) (1+cost)dt =π+2[sint]_0 ^(π/2) =π +2](Q124667.png)
Answered by MJS_new last updated on 05/Dec/20
![∫_0 ^2 (√((2+x)/(2−x)))dx= [t=(√((2−x)/(2+x))) → dx=−(1/2)(x+2)^(3/2) (√(2−x))dt] =8∫_0 ^1 (dt/((t^2 +1)^2 ))=[((4t)/(t^2 +1))+4arctan t]_0 ^1 =π+2](Q124732.png)
| ||
Question and Answers Forum | ||
Question Number 124632 by liberty last updated on 05/Dec/20 | ||
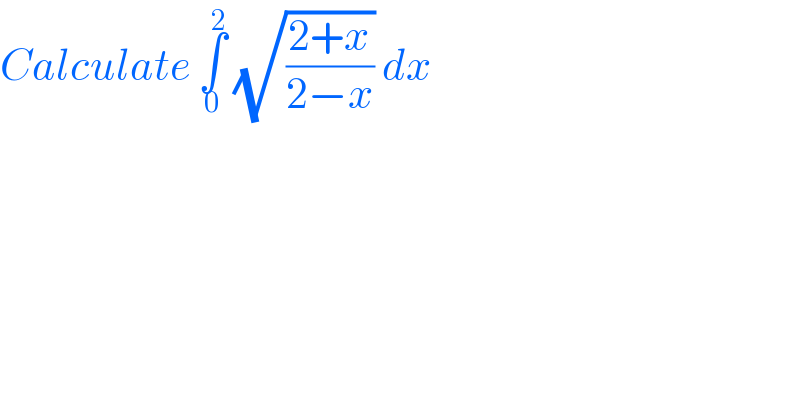 | ||
Answered by bemath last updated on 05/Dec/20 | ||
![put x=2cos 2θ I=∫_(π/4) ^0 (√((2+2cos 2θ)/(2−2cos 2θ))) (−4sin 2θ) dθ I= 4∫_0 ^(π/4) (√((1+cos 2θ)/(1−cos 2θ))) (2sin θ cos θ)dθ I= 4∫_0 ^(π/4) 2cos^2 θ dθ I=4 [ ((sin 2θ)/2) + θ ]_( 0) ^(π/4) = 4((1/2)+(π/4)) I=2+π](Q124633.png) | ||
| ||
Answered by mathmax by abdo last updated on 05/Dec/20 | ||
![A =∫_0 ^2 (√((2+x)/(2−x)))dx we do the changement x=2cost ⇒ A =∫_(π/2) ^0 (√((1+cost)/(1−cost)))(−2sint)dt =2∫_0 ^(π/2) ((cos((t/2)))/(sin((t/2))))×2cos((t/2))sin((t/2))dt =4 ∫_0 ^(π/2) cos^2 ((t/2))dt =4∫_0 ^(π/2) ((1+cost)/2)dt =2∫_0 ^(π/2) (1+cost)dt =π+2[sint]_0 ^(π/2) =π +2](Q124667.png) | ||
| ||
Answered by MJS_new last updated on 05/Dec/20 | ||
![∫_0 ^2 (√((2+x)/(2−x)))dx= [t=(√((2−x)/(2+x))) → dx=−(1/2)(x+2)^(3/2) (√(2−x))dt] =8∫_0 ^1 (dt/((t^2 +1)^2 ))=[((4t)/(t^2 +1))+4arctan t]_0 ^1 =π+2](Q124732.png) | ||
| ||