Question and Answers Forum
Question Number 124821 by ajfour last updated on 06/Dec/20
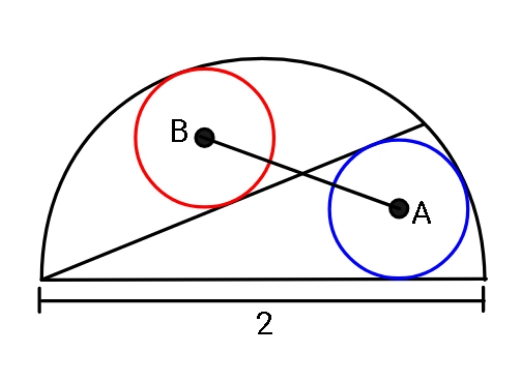
Commented by ajfour last updated on 06/Dec/20

Commented by ajfour last updated on 06/Dec/20
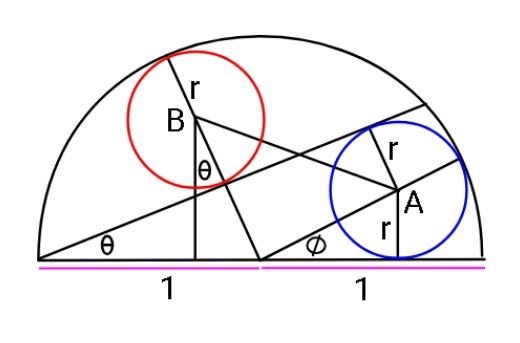
Answered by mr W last updated on 06/Dec/20
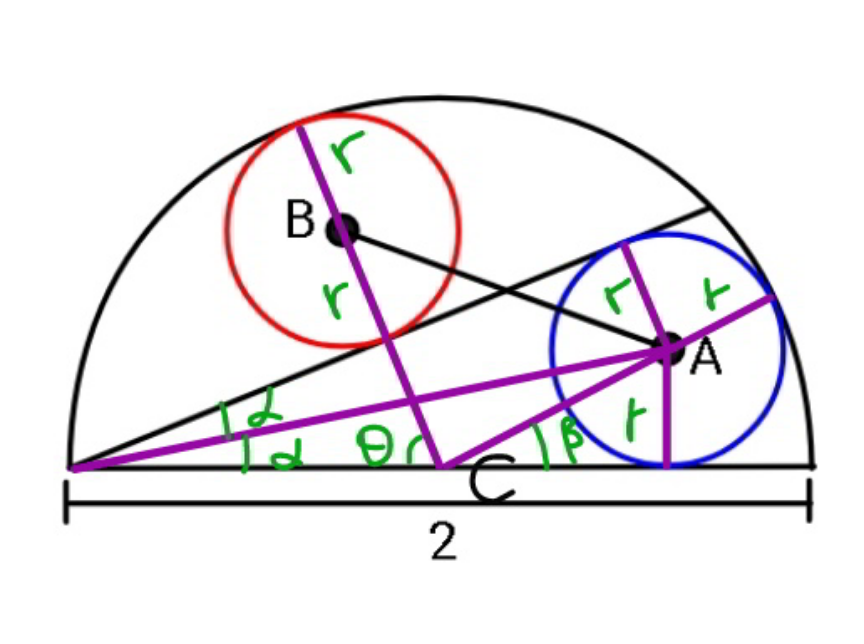
Commented by mr W last updated on 06/Dec/20
![R=1=radius of semicircle let λ=(r/R) cos θ=((R−2r)/R)=1−2λ tan α=(r/(R+(√((R−r)^2 −r^2 ))))=(λ/(1+(√(1−2λ)))) 2α=(π/2)−θ tan 2α=(1/(tan θ)) ((2×(λ/(1+(√(1−2λ)))))/(1−((λ/(1+(√(1−2λ)))))^2 ))=((1−2λ)/( (√(1−(1−2λ)^2 )))) ((2λ(1+(√(1−2λ))))/((1+(√(1−2λ)))^2 −λ^2 ))=((1−2λ)/( (√(1−(1−2λ)^2 )))) ⇒λ≈0.3129 sin β=(r/(R−r))=(λ/(1−λ)) AB=2(R−r)sin ((π−θ−β)/2) ((AB)/R)=2(1−λ)cos ((θ+β)/2) =2(1−λ)cos (1/2)[cos^(−1) (1−2λ)+sin^(−1) ((λ/(1−λ)))] ≈0.9274](Q124844.png)
Commented by MJS_new last updated on 06/Dec/20
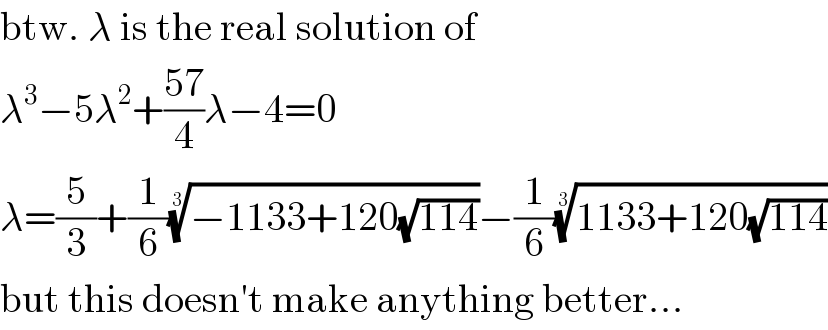
Commented by mr W last updated on 06/Dec/20
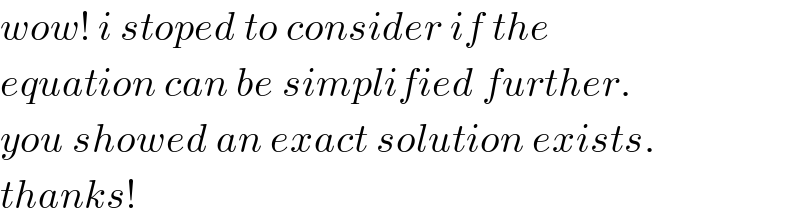
Commented by MJS_new last updated on 06/Dec/20
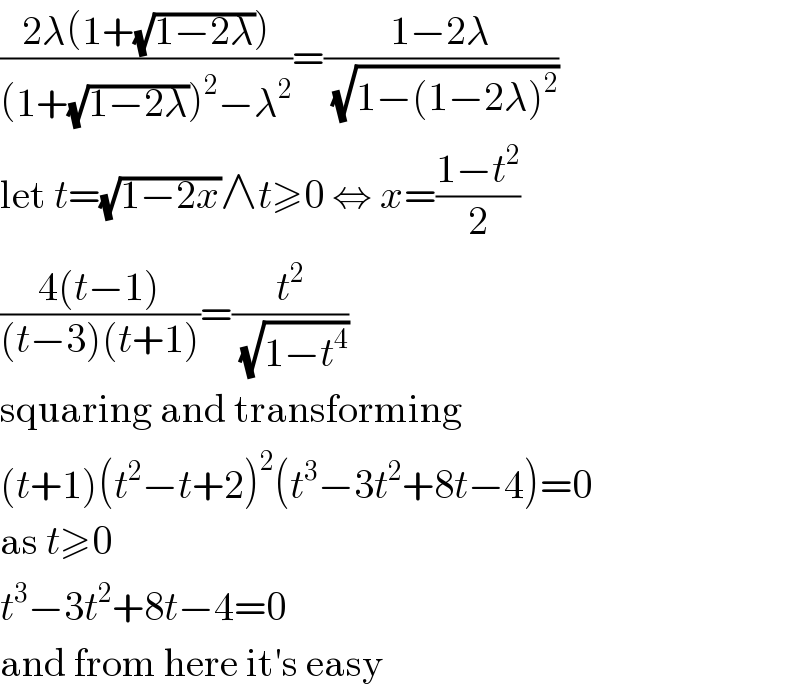
Commented by ajfour last updated on 06/Dec/20