Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 124831 by mnjuly1970 last updated on 06/Dec/20

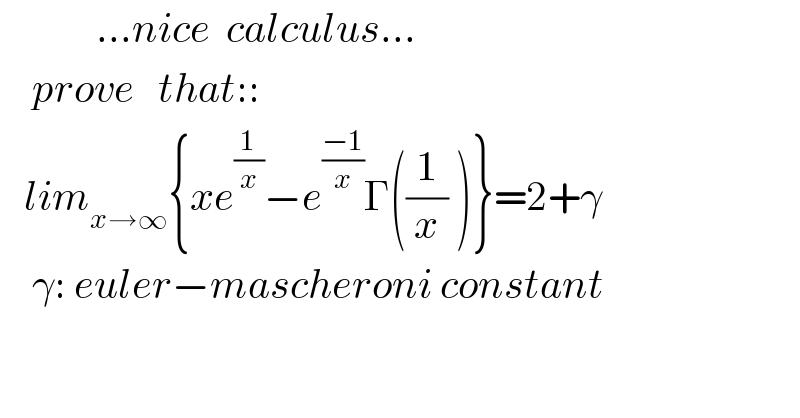
...nice calculus... prove that:: lim_(x→∞) {xe^(1/x) −e^((−1)/x) Γ((1/x) )}=2+γ γ: euler−mascheroni constant

$$\:\:\:\:\:\:\:\:\:\:\:\:...{nice}\:\:{calculus}... \\ $$$$\:\:\:\:{prove}\:\:\:{that}:: \\ $$$$\:\:\:{lim}_{{x}\rightarrow\infty} \left\{{xe}^{\frac{\mathrm{1}}{{x}}} −{e}^{\frac{−\mathrm{1}}{{x}}} \Gamma\left(\frac{\mathrm{1}}{{x}}\:\right)\right\}=\mathrm{2}+\gamma \\ $$$$\:\:\:\:\gamma:\:{euler}−{mascheroni}\:{constant} \\ $$$$ \\ $$

Answered by Dwaipayan Shikari last updated on 06/Dec/20

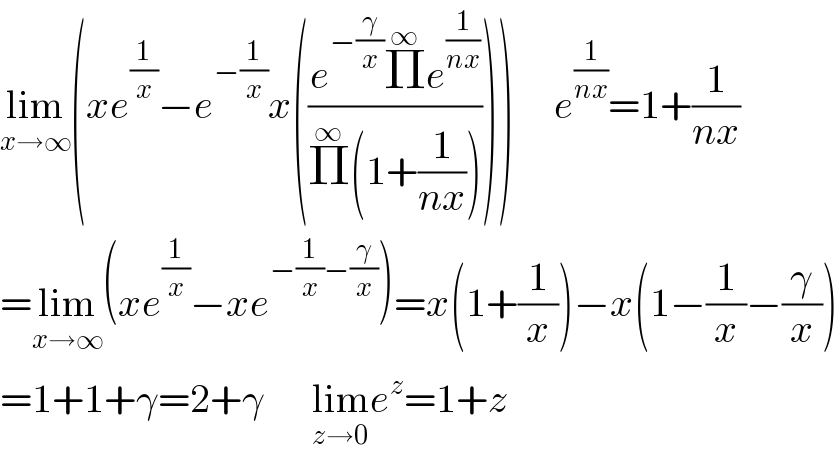
lim_(x→∞) (xe^(1/x) −e^(−(1/x)) x(((e^(−(γ/x)) Π^∞ e^(1/(nx)) )/(Π^∞ (1+(1/(nx))))))) e^(1/(nx)) =1+(1/(nx)) =lim_(x→∞) (xe^(1/x) −xe^(−(1/x)−(γ/x)) )=x(1+(1/x))−x(1−(1/x)−(γ/x)) =1+1+γ=2+γ lim_(z→0) e^z =1+z

$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left({xe}^{\frac{\mathrm{1}}{{x}}} −{e}^{−\frac{\mathrm{1}}{{x}}} {x}\left(\frac{{e}^{−\frac{\gamma}{{x}}} \overset{\infty} {\prod}{e}^{\frac{\mathrm{1}}{{nx}}} }{\overset{\infty} {\prod}\left(\mathrm{1}+\frac{\mathrm{1}}{{nx}}\right)}\right)\right)\:\:\:\:\:{e}^{\frac{\mathrm{1}}{{nx}}} =\mathrm{1}+\frac{\mathrm{1}}{{nx}} \\ $$$$=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left({xe}^{\frac{\mathrm{1}}{{x}}} −{xe}^{−\frac{\mathrm{1}}{{x}}−\frac{\gamma}{{x}}} \right)={x}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)−{x}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}−\frac{\gamma}{{x}}\right) \\ $$$$=\mathrm{1}+\mathrm{1}+\gamma=\mathrm{2}+\gamma\:\:\:\:\:\:\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}{e}^{{z}} =\mathrm{1}+{z} \\ $$

Commented by mnjuly1970 last updated on 06/Dec/20

thank you excellent....

$${thank}\:{you} \\ $$$${excellent}.... \\ $$

Commented by Dwaipayan Shikari last updated on 06/Dec/20

Great sir! :)

$$\left.{Great}\:{sir}!\:\::\right) \\ $$

Answered by mindispower last updated on 06/Dec/20

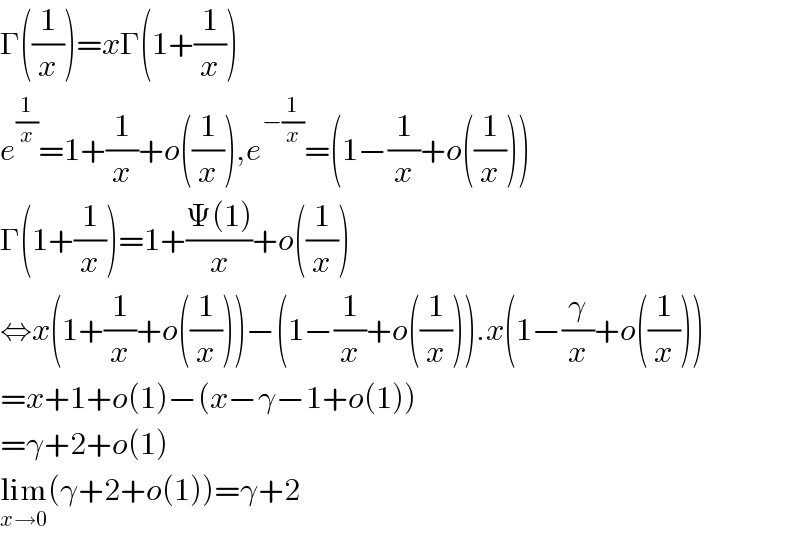
Γ((1/x))=xΓ(1+(1/x)) e^(1/x) =1+(1/x)+o((1/x)),e^(−(1/x)) =(1−(1/x)+o((1/x))) Γ(1+(1/x))=1+((Ψ(1))/x)+o((1/x)) ⇔x(1+(1/x)+o((1/x)))−(1−(1/x)+o((1/x))).x(1−(γ/x)+o((1/x))) =x+1+o(1)−(x−γ−1+o(1)) =γ+2+o(1) lim_(x→0) (γ+2+o(1))=γ+2

$$\Gamma\left(\frac{\mathrm{1}}{{x}}\right)={x}\Gamma\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right) \\ $$$${e}^{\frac{\mathrm{1}}{{x}}} =\mathrm{1}+\frac{\mathrm{1}}{{x}}+{o}\left(\frac{\mathrm{1}}{{x}}\right),{e}^{−\frac{\mathrm{1}}{{x}}} =\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}+{o}\left(\frac{\mathrm{1}}{{x}}\right)\right) \\ $$$$\Gamma\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)=\mathrm{1}+\frac{\Psi\left(\mathrm{1}\right)}{{x}}+{o}\left(\frac{\mathrm{1}}{{x}}\right) \\ $$$$\Leftrightarrow{x}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}+{o}\left(\frac{\mathrm{1}}{{x}}\right)\right)−\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}+{o}\left(\frac{\mathrm{1}}{{x}}\right)\right).{x}\left(\mathrm{1}−\frac{\gamma}{{x}}+{o}\left(\frac{\mathrm{1}}{{x}}\right)\right)\: \\ $$$$={x}+\mathrm{1}+{o}\left(\mathrm{1}\right)−\left({x}−\gamma−\mathrm{1}+{o}\left(\mathrm{1}\right)\right) \\ $$$$=\gamma+\mathrm{2}+{o}\left(\mathrm{1}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\gamma+\mathrm{2}+{o}\left(\mathrm{1}\right)\right)=\gamma+\mathrm{2} \\ $$

Commented by mnjuly1970 last updated on 06/Dec/20

thanks alot sir Powr..

$${thanks}\:{alot}\:{sir}\:{Powr}.. \\ $$

Answered by mnjuly1970 last updated on 06/Dec/20

(1/x)=_(t→0) ^(x→∞) t lim_(t→0) [(1/t)e^t −e^(−t) Γ(t)] =lim_(t→0) (((e^t −e^(−t) Γ(t+1))/t)) =_(rule) ^(hopital) lim_(t→0) (((e^t +e^(−t) Γ(t+1)−Γ′(t+1)e^(−t) )/1)) =1+1−ψ(1)=2−(−γ)=2+γ ✓

$$\frac{\mathrm{1}}{{x}}\underset{{t}\rightarrow\mathrm{0}} {\overset{{x}\rightarrow\infty} {=}}{t} \\ $$$$\:\:{lim}_{{t}\rightarrow\mathrm{0}} \left[\frac{\mathrm{1}}{{t}}{e}^{{t}} −{e}^{−{t}} \Gamma\left({t}\right)\right] \\ $$$$\:\:={lim}_{{t}\rightarrow\mathrm{0}} \left(\frac{{e}^{{t}} −{e}^{−{t}} \Gamma\left({t}+\mathrm{1}\right)}{{t}}\right) \\ $$$$\:\underset{{rule}} {\overset{{hopital}} {=}}{lim}_{{t}\rightarrow\mathrm{0}} \left(\frac{{e}^{{t}} +{e}^{−{t}} \Gamma\left({t}+\mathrm{1}\right)−\Gamma'\left({t}+\mathrm{1}\right){e}^{−{t}} }{\mathrm{1}}\right) \\ $$$$=\mathrm{1}+\mathrm{1}−\psi\left(\mathrm{1}\right)=\mathrm{2}−\left(−\gamma\right)=\mathrm{2}+\gamma\:\checkmark \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com