Question Number 124979 by mathmax by abdo last updated on 07/Dec/20
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{arctan}\left(\mathrm{x}^{\mathrm{n}} \right)\:\mathrm{with}\:\mathrm{n}\:\mathrm{natural} \\ $$$$\left.\mathrm{1}\right)\:\mathrm{find}\:\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{0}\right)\:\mathrm{and}\:\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{1}\right) \\ $$$$\left.\mathrm{2}\right)\mathrm{developp}\:\mathrm{f}\:\mathrm{at}\:\mathrm{integr}\:\mathrm{serie} \\ $$$$\left.\mathrm{3}\right)\mathrm{calculte}\:\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{f}\left(\mathrm{x}\right)}{\mathrm{x}^{\mathrm{n}} }\mathrm{dx}\:\mathrm{with}\:\mathrm{n}\geqslant\mathrm{2} \\ $$
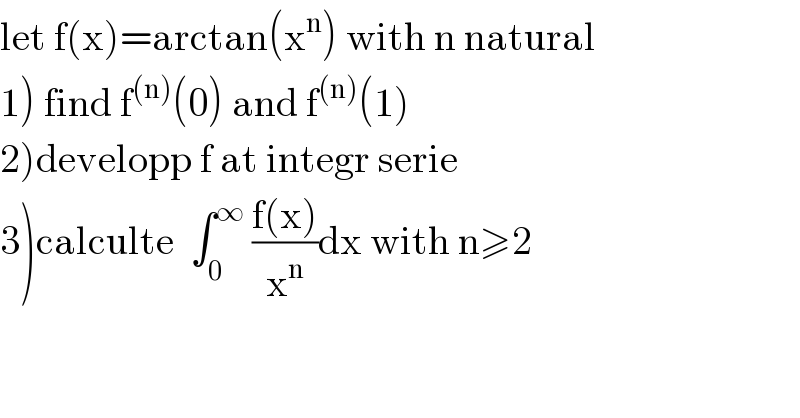
Answered by Dwaipayan Shikari last updated on 07/Dec/20
![f(x)=tan^(−1) x^n ∫_0 ^∞ ((tan^(−1) x^n )/x^n )dx=−[n((tan^(−1) x^n )/x^(n−1) )]_0 ^∞ +n^2 ∫_0 ^∞ x^(1−n) (x^(n−1) /(1+x^(2n) )) dx =n^2 ∫_0 ^∞ (dx/(1+x^(2n) )) x^(2n) =t⇒2n x^(2n−1) =(dt/dx) =(n/2)∫_0 ^∞ x^(1−2n) (1/(1+t))dt=(n/2)∫_0 ^∞ t^((1/(2n))−1) (1/(1+t))dt (t/(1+t))=u⇒(1/((1+t)^2 ))=(du/dt) =(n/2)∫_0 ^1 (u^((1/(2n))−1) /((1−u)^((1/(2n))−1) ))(1−u)^(−1) du (u/(1−u))=t =(n/2)∫_0 ^1 u^((1/(2n))−1) (1−u)^(−(1/(2n))) du =(n/2)Γ((1/(2n)))Γ(1−(1/(2n)))=(n/2).(π/(sin((π/(2n)))))](Q124987.png)
$${f}\left({x}\right)={tan}^{−\mathrm{1}} {x}^{{n}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{tan}^{−\mathrm{1}} {x}^{{n}} }{{x}^{{n}} }{dx}=−\left[{n}\frac{{tan}^{−\mathrm{1}} {x}^{{n}} }{{x}^{{n}−\mathrm{1}} }\right]_{\mathrm{0}} ^{\infty} +{n}^{\mathrm{2}} \int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{1}−{n}} \frac{{x}^{{n}−\mathrm{1}} }{\mathrm{1}+{x}^{\mathrm{2}{n}} }\:{dx} \\ $$$$={n}^{\mathrm{2}} \int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}{n}} }\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}{n}} ={t}\Rightarrow\mathrm{2}{n}\:{x}^{\mathrm{2}{n}−\mathrm{1}} =\frac{{dt}}{{dx}} \\ $$$$=\frac{{n}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{1}−\mathrm{2}{n}} \frac{\mathrm{1}}{\mathrm{1}+{t}}{dt}=\frac{{n}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} {t}^{\frac{\mathrm{1}}{\mathrm{2}{n}}−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{t}}{dt}\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{t}}{\mathrm{1}+{t}}={u}\Rightarrow\frac{\mathrm{1}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }=\frac{{du}}{{dt}} \\ $$$$=\frac{{n}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{u}^{\frac{\mathrm{1}}{\mathrm{2}{n}}−\mathrm{1}} }{\left(\mathrm{1}−{u}\right)^{\frac{\mathrm{1}}{\mathrm{2}{n}}−\mathrm{1}} }\left(\mathrm{1}−{u}\right)^{−\mathrm{1}} {du}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{u}}{\mathrm{1}−{u}}={t} \\ $$$$=\frac{{n}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} {u}^{\frac{\mathrm{1}}{\mathrm{2}{n}}−\mathrm{1}} \left(\mathrm{1}−{u}\right)^{−\frac{\mathrm{1}}{\mathrm{2}{n}}} \:{du}\:\:=\frac{{n}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}{n}}\right)\Gamma\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{n}}\right)=\frac{{n}}{\mathrm{2}}.\frac{\pi}{{sin}\left(\frac{\pi}{\mathrm{2}{n}}\right)}\: \\ $$
Answered by mathmax by abdo last updated on 07/Dec/20
![1) f(x)=arctan(x^n ) ⇒f^((1)) (x)=((nx^(n−1) )/(1+x^(2n) )) ⇒ f^((p)) (x)=n((x^(n−1) /(x^(2n) +1)))^((p−1)) with p≥1 let decompose F(x) =(x^(n−1) /(x^(2n) +1)) z^(2n) +1=0 ⇒z^(2n) =e^(i(2k+1)π) ⇒z_k =e^(i(((2k+1)π)/(2n))) and k∈[[0,2n−1]] ⇒ F(x)=(x^(n−1) /(Π_(k=0) ^(2n−1) (x−z_k ))) =Σ_(k=0) ^(2n−1) (a_k /(x−z_k )) we have a_k =(z_k ^(n−1) /(2n z_k ^(2n−1) )) =(1/(2n))×(z_k ^n /((−1)))=−(1/(2n))z_k ^n =−(1/(2n))×e^(i(((2k+1)π)/2)) =−(1/(2n)) e^(ikπ) e^((iπ)/2) =−(1/(2n))(−1)^k i=((i(−1)^k )/(2n)) ⇒F(x)=(i/(2n))Σ_(k=0) ^(2n−1) (((−1)^k )/(x−z_k )) ⇒ f^((p)) (x)=(i/2)Σ_(k=0) ^(2n−1) (−1)^k {(1/(x−z_k ))}^((p−1)) =(i/2)Σ_(k=0) ^(2n−1) (−1)^(k ) (((−1)^(p−1) (p−1)!)/((x−z_k )^p )) ⇒ f^((n)) (x)=(i/2)Σ_(k=0) ^(2n−1) (−1)^k ×(((−1)^(n−1) (n−1)!)/((x−z_k )^n )) ⇒ f^((n)) (0) =((i(−1)^(n−1) )/2)(n−1)!Σ_(k=0) ^(2n−1) (((−1)^k )/((−z_k )^n )) =−(i/2)(n−1)! Σ_(k=0) ^(2n−1) (((−1)^k )/z_k ^n ) f^((n)) (1) =(i/2)Σ_(k=0) ^(2n−1) (−1)^k (((−1)^(n−1) (n−1)!)/((1−z_k )^n ))](Q125038.png)
$$\left.\mathrm{1}\right)\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{arctan}\left(\mathrm{x}^{\mathrm{n}} \right)\:\Rightarrow\mathrm{f}^{\left(\mathrm{1}\right)} \left(\mathrm{x}\right)=\frac{\mathrm{nx}^{\mathrm{n}−\mathrm{1}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2n}} }\:\Rightarrow \\ $$$$\mathrm{f}^{\left(\mathrm{p}\right)} \left(\mathrm{x}\right)=\mathrm{n}\left(\frac{\mathrm{x}^{\mathrm{n}−\mathrm{1}} }{\mathrm{x}^{\mathrm{2n}} +\mathrm{1}}\right)^{\left(\mathrm{p}−\mathrm{1}\right)} \:\:\mathrm{with}\:\mathrm{p}\geqslant\mathrm{1} \\ $$$$\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{x}\right)\:=\frac{\mathrm{x}^{\mathrm{n}−\mathrm{1}} }{\mathrm{x}^{\mathrm{2n}} +\mathrm{1}} \\ $$$$\mathrm{z}^{\mathrm{2n}} +\mathrm{1}=\mathrm{0}\:\Rightarrow\mathrm{z}^{\mathrm{2n}} \:=\mathrm{e}^{\mathrm{i}\left(\mathrm{2k}+\mathrm{1}\right)\pi} \:\Rightarrow\mathrm{z}_{\mathrm{k}} =\mathrm{e}^{\mathrm{i}\frac{\left(\mathrm{2k}+\mathrm{1}\right)\pi}{\mathrm{2n}}} \:\:\mathrm{and}\:\mathrm{k}\in\left[\left[\mathrm{0},\mathrm{2n}−\mathrm{1}\right]\right]\:\Rightarrow \\ $$$$\mathrm{F}\left(\mathrm{x}\right)=\frac{\mathrm{x}^{\mathrm{n}−\mathrm{1}} }{\prod_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}−\mathrm{1}} \left(\mathrm{x}−\mathrm{z}_{\mathrm{k}} \right)}\:=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}−\mathrm{1}} \:\frac{\mathrm{a}_{\mathrm{k}} }{\mathrm{x}−\mathrm{z}_{\mathrm{k}} }\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{a}_{\mathrm{k}} =\frac{\mathrm{z}_{\mathrm{k}} ^{\mathrm{n}−\mathrm{1}} }{\mathrm{2n}\:\mathrm{z}_{\mathrm{k}} ^{\mathrm{2n}−\mathrm{1}} }\:=\frac{\mathrm{1}}{\mathrm{2n}}×\frac{\mathrm{z}_{\mathrm{k}} ^{\mathrm{n}} }{\left(−\mathrm{1}\right)}=−\frac{\mathrm{1}}{\mathrm{2n}}\mathrm{z}_{\mathrm{k}} ^{\mathrm{n}} \:=−\frac{\mathrm{1}}{\mathrm{2n}}×\mathrm{e}^{\mathrm{i}\frac{\left(\mathrm{2k}+\mathrm{1}\right)\pi}{\mathrm{2}}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2n}}\:\mathrm{e}^{\mathrm{ik}\pi} \:\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{2}}} \:=−\frac{\mathrm{1}}{\mathrm{2n}}\left(−\mathrm{1}\right)^{\mathrm{k}} \mathrm{i}=\frac{\mathrm{i}\left(−\mathrm{1}\right)^{\mathrm{k}} }{\mathrm{2n}}\:\Rightarrow\mathrm{F}\left(\mathrm{x}\right)=\frac{\mathrm{i}}{\mathrm{2n}}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}−\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\mathrm{x}−\mathrm{z}_{\mathrm{k}} }\:\Rightarrow \\ $$$$\mathrm{f}^{\left(\mathrm{p}\right)} \left(\mathrm{x}\right)=\frac{\mathrm{i}}{\mathrm{2}}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}−\mathrm{1}} \left(−\mathrm{1}\right)^{\mathrm{k}} \left\{\frac{\mathrm{1}}{\mathrm{x}−\mathrm{z}_{\mathrm{k}} }\right\}^{\left(\mathrm{p}−\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{i}}{\mathrm{2}}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}−\mathrm{1}} \left(−\mathrm{1}\right)^{\mathrm{k}\:\:} \:\:\frac{\left(−\mathrm{1}\right)^{\mathrm{p}−\mathrm{1}} \left(\mathrm{p}−\mathrm{1}\right)!}{\left(\mathrm{x}−\mathrm{z}_{\mathrm{k}} \right)^{\mathrm{p}} }\:\Rightarrow \\ $$$$\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)=\frac{\mathrm{i}}{\mathrm{2}}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}−\mathrm{1}} \left(−\mathrm{1}\right)^{\mathrm{k}} ×\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \left(\mathrm{n}−\mathrm{1}\right)!}{\left(\mathrm{x}−\mathrm{z}_{\mathrm{k}} \right)^{\mathrm{n}} }\:\Rightarrow \\ $$$$\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{0}\right)\:=\frac{\mathrm{i}\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{2}}\left(\mathrm{n}−\mathrm{1}\right)!\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}−\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\left(−\mathrm{z}_{\mathrm{k}} \right)^{\mathrm{n}} }\: \\ $$$$=−\frac{\mathrm{i}}{\mathrm{2}}\left(\mathrm{n}−\mathrm{1}\right)!\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}−\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\mathrm{z}_{\mathrm{k}} ^{\mathrm{n}} } \\ $$$$\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{1}\right)\:=\frac{\mathrm{i}}{\mathrm{2}}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}−\mathrm{1}} \left(−\mathrm{1}\right)^{\mathrm{k}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \left(\mathrm{n}−\mathrm{1}\right)!}{\left(\mathrm{1}−\mathrm{z}_{\mathrm{k}} \right)^{\mathrm{n}} } \\ $$
Answered by mathmax by abdo last updated on 07/Dec/20
$$\left.\mathrm{2}\right)\:\mathrm{f}\left(\mathrm{x}\right)=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{0}\right)}{\mathrm{n}!}\mathrm{x}^{\mathrm{n}} \:\:\:\mathrm{and}\:\mathrm{f}^{\left.\right)\left.\mathrm{n}\right)} \left(\mathrm{0}\right)\:\mathrm{is}\:\mathrm{known} \\ $$
Answered by mathmax by abdo last updated on 07/Dec/20
![3) A_n =∫_0 ^∞ ((f(x))/x^n )dx ⇒ A_n =∫_0 ^∞ ((arctan(x^n ))/x^n )dx =∫_0 ^∞ x^(−n) arctan(x^n )dx by psrts A_n =[(1/(1−n))x^(1−n) arctan(x^n )]_0 ^∞ −∫_0 ^∞ (1/(1−n))x^(1−n) ×((nx^(n−1) )/(1+x^(2n) ))dx =(n/(n−1))∫_0 ^∞ (dx/(1+x^(2n) )) but ∫_0 ^∞ (dx/(1+x^(2n) ))=_(x^(2n) =t→x=t^(1/(2n)) ) ∫_0 ^∞ (1/(2n))t^((1/(2n))−1) (dt/(1+t)) =(1/(2n))∫_0 ^∞ (t^((1/(2n))−1) /(1+t))dt =(1/(2n))×(π/(sin((π/(2n))))) ⇒A_n =(n/(n−1))×(π/(2nsin((π/(2n))))) ⇒ A_n =(π/(2(n−1)sin((π/(2n))))) (n≥2)](Q125040.png)
$$\left.\mathrm{3}\right)\:\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{f}\left(\mathrm{x}\right)}{\mathrm{x}^{\mathrm{n}} }\mathrm{dx}\:\Rightarrow\:\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{arctan}\left(\mathrm{x}^{\mathrm{n}} \right)}{\mathrm{x}^{\mathrm{n}} }\mathrm{dx}\:=\int_{\mathrm{0}} ^{\infty} \mathrm{x}^{−\mathrm{n}} \:\mathrm{arctan}\left(\mathrm{x}^{\mathrm{n}} \right)\mathrm{dx} \\ $$$$\mathrm{by}\:\mathrm{psrts}\:\mathrm{A}_{\mathrm{n}} =\left[\frac{\mathrm{1}}{\mathrm{1}−\mathrm{n}}\mathrm{x}^{\mathrm{1}−\mathrm{n}} \:\mathrm{arctan}\left(\mathrm{x}^{\mathrm{n}} \right)\right]_{\mathrm{0}} ^{\infty} −\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{1}−\mathrm{n}}\mathrm{x}^{\mathrm{1}−\mathrm{n}} ×\frac{\mathrm{nx}^{\mathrm{n}−\mathrm{1}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2n}} }\mathrm{dx} \\ $$$$=\frac{\mathrm{n}}{\mathrm{n}−\mathrm{1}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2n}} }\:\:\mathrm{but}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2n}} }=_{\mathrm{x}^{\mathrm{2n}} =\mathrm{t}\rightarrow\mathrm{x}=\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{2n}}} } \:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\mathrm{2n}}\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{2n}}−\mathrm{1}} \:\:\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2n}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{2n}}−\mathrm{1}} }{\mathrm{1}+\mathrm{t}}\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2n}}×\frac{\pi}{\mathrm{sin}\left(\frac{\pi}{\mathrm{2n}}\right)}\:\Rightarrow\mathrm{A}_{\mathrm{n}} =\frac{\mathrm{n}}{\mathrm{n}−\mathrm{1}}×\frac{\pi}{\mathrm{2nsin}\left(\frac{\pi}{\mathrm{2n}}\right)} \\ $$$$\Rightarrow\:\mathrm{A}_{\mathrm{n}} =\frac{\pi}{\mathrm{2}\left(\mathrm{n}−\mathrm{1}\right)\mathrm{sin}\left(\frac{\pi}{\mathrm{2n}}\right)}\:\:\:\left(\mathrm{n}\geqslant\mathrm{2}\right) \\ $$