Question Number 125084 by ajfour last updated on 08/Dec/20
Commented by ajfour last updated on 08/Dec/20
$${Find}\:{x},\:{hence}\:{radius}\:{of}\:{circle}. \\ $$
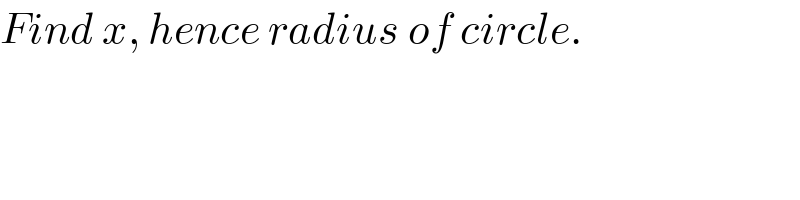
Commented by ajfour last updated on 08/Dec/20
Commented by mr W last updated on 08/Dec/20
$${x}\:{can}\:{be}\:{any}\:{value},\:{because}\:{the}\:{shape} \\ $$$${formed}\:{by}\:{both}\:{rectangles}\:{is}\:{always} \\ $$$${cyclic}. \\ $$
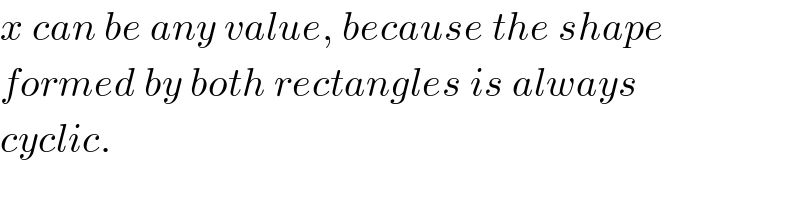
Answered by mr W last updated on 08/Dec/20
Commented by mr W last updated on 08/Dec/20
![ABCD is always cyclic. AB=CD=(√((((x−1)/2))^2 +(1+x)^2 )) AC=BD=(√((((x+1)/2))^2 +(1+x)^2 ))=(((x+1)(√5))/2) R=radius Δ_(ABD) =((1×(1+x))/2) formula R=((abc)/(4Δ)) ⇒R=((√([(((x−1)/2))^2 +(1+x)^2 ][(((x+1)/2))^2 +(1+x)^2 ]))/(2(1+x))) ⇒R=((√(5(5x^2 +6x+5)))/8)](Q125111.png)
$${ABCD}\:{is}\:{always}\:{cyclic}. \\ $$$${AB}={CD}=\sqrt{\left(\frac{{x}−\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\mathrm{1}+{x}\right)^{\mathrm{2}} } \\ $$$${AC}={BD}=\sqrt{\left(\frac{{x}+\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }=\frac{\left({x}+\mathrm{1}\right)\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${R}={radius} \\ $$$$\Delta_{{ABD}} =\frac{\mathrm{1}×\left(\mathrm{1}+{x}\right)}{\mathrm{2}} \\ $$$${formula}\:{R}=\frac{{abc}}{\mathrm{4}\Delta} \\ $$$$\Rightarrow{R}=\frac{\sqrt{\left[\left(\frac{{x}−\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\mathrm{1}+{x}\right)^{\mathrm{2}} \right]\left[\left(\frac{{x}+\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\mathrm{1}+{x}\right)^{\mathrm{2}} \right]}}{\mathrm{2}\left(\mathrm{1}+{x}\right)} \\ $$$$\Rightarrow{R}=\frac{\sqrt{\mathrm{5}\left(\mathrm{5}{x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{5}\right)}}{\mathrm{8}} \\ $$
Commented by ajfour last updated on 08/Dec/20
$${Very}\:{Nice}\:{solution},\:{Sir}! \\ $$