Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 125114 by bramlexs22 last updated on 08/Dec/20

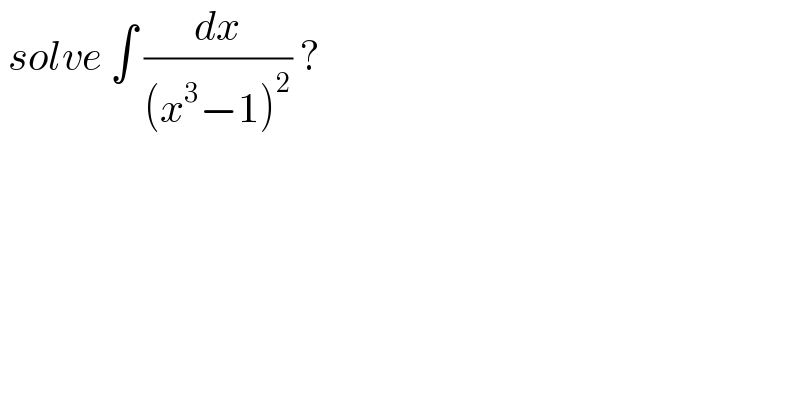
solve ∫ (dx/((x^3 −1)^2 )) ?

$$\:{solve}\:\int\:\frac{{dx}}{\left({x}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{2}} }\:? \\ $$

Commented by liberty last updated on 08/Dec/20

Ostrogradsky′s method ( Prof sir MJS )

$${Ostrogradsky}'{s}\:{method}\:\left(\:{Prof}\:{sir}\:{MJS}\:\right) \\ $$

Answered by liberty last updated on 08/Dec/20

equation has the form ∫ (dx/((x^3 −1)^2 )) = ((ax^2 +bx+c)/(x^3 −1))+∫ ((ex^2 +fx+g)/(x^3 −1)) dx differentiating both side we have (1/((x^3 −1)^2 )) = (((x^3 −1)(2ax+b)−(ax^2 +bx+c)3x^2 )/((x^3 −1)^2 )) + ((ex^2 +fx+g)/(x^3 −1)) equating the coefficients gives e = 0 , a=0 , c=0 , b=−(1/3) , f=0 , g=−(2/3) I= ∫(dx/((x^3 −1)^2 )) = ((−(1/3)x)/(x^3 −1)) + ∫ (((−2)/3)/(x^3 −1)) dx = ((−x)/(3(x^3 −1)))+ ∫ [ ((−(2/9))/(x−1)) + (((2/9)x+(4/9))/(x^2 +x+1)) ]dx = −(x/(3(x^3 −1)))−(2/9)ln ∣x−1∣ + (1/9)ln ∣x^2 +x+1∣ + ((2(√3))/9) arc tan (((2x+1)/( (√3)))) + c

$${equation}\:{has}\:{the}\:{form}\:\int\:\frac{{dx}}{\left({x}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{2}} }\:=\:\frac{{ax}^{\mathrm{2}} +{bx}+{c}}{{x}^{\mathrm{3}} −\mathrm{1}}+\int\:\frac{{ex}^{\mathrm{2}} +{fx}+{g}}{{x}^{\mathrm{3}} −\mathrm{1}}\:{dx} \\ $$$${differentiating}\:{both}\:{side}\:{we}\:{have} \\ $$$$\frac{\mathrm{1}}{\left({x}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{2}} }\:=\:\frac{\left({x}^{\mathrm{3}} −\mathrm{1}\right)\left(\mathrm{2}{ax}+{b}\right)−\left({ax}^{\mathrm{2}} +{bx}+{c}\right)\mathrm{3}{x}^{\mathrm{2}} }{\left({x}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{2}} }\:+\:\frac{{ex}^{\mathrm{2}} +{fx}+{g}}{{x}^{\mathrm{3}} −\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$${equating}\:{the}\:{coefficients}\:{gives} \\ $$$${e}\:=\:\mathrm{0}\:,\:{a}=\mathrm{0}\:,\:{c}=\mathrm{0}\:,\:{b}=−\frac{\mathrm{1}}{\mathrm{3}}\:,\:{f}=\mathrm{0}\:,\:{g}=−\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${I}=\:\int\frac{{dx}}{\left({x}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{2}} }\:=\:\frac{−\frac{\mathrm{1}}{\mathrm{3}}{x}}{{x}^{\mathrm{3}} −\mathrm{1}}\:+\:\int\:\frac{\frac{−\mathrm{2}}{\mathrm{3}}}{{x}^{\mathrm{3}} −\mathrm{1}}\:{dx} \\ $$$$\:=\:\frac{−{x}}{\mathrm{3}\left({x}^{\mathrm{3}} −\mathrm{1}\right)}+\:\int\:\left[\:\frac{−\frac{\mathrm{2}}{\mathrm{9}}}{{x}−\mathrm{1}}\:+\:\frac{\frac{\mathrm{2}}{\mathrm{9}}{x}+\frac{\mathrm{4}}{\mathrm{9}}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\:\right]{dx} \\ $$$$\:=\:−\frac{{x}}{\mathrm{3}\left({x}^{\mathrm{3}} −\mathrm{1}\right)}−\frac{\mathrm{2}}{\mathrm{9}}\mathrm{ln}\:\mid{x}−\mathrm{1}\mid\:+\:\frac{\mathrm{1}}{\mathrm{9}}\mathrm{ln}\:\mid{x}^{\mathrm{2}} +{x}+\mathrm{1}\mid \\ $$$$\:+\:\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{9}}\:\mathrm{arc}\:\mathrm{tan}\:\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\:+\:{c}\: \\ $$

Commented by bramlexs22 last updated on 08/Dec/20

thank you sir

$${thank}\:{you}\:{sir} \\ $$

Commented by MJS_new last updated on 08/Dec/20

yesss!

$$\mathrm{yesss}! \\ $$

Commented by bramlexs22 last updated on 08/Dec/20

does anyone have a pdf file about this method

Commented by MJS_new last updated on 08/Dec/20

search for “Ostrogradski Method” on the www, plenty of explanations...

$$\mathrm{search}\:\mathrm{for}\:``\mathrm{Ostrogradski}\:\mathrm{Method}''\:\mathrm{on}\:\mathrm{the} \\ $$$$\mathrm{www},\:\mathrm{plenty}\:\mathrm{of}\:\mathrm{explanations}... \\ $$

Commented by Ar Brandon last updated on 08/Dec/20

well detailed��

Answered by mathmax by abdo last updated on 08/Dec/20

A =∫ (dx/((x^3 −1)^2 )) let f(λ)=∫ (dx/(x^3 −λ^3 )) (λ>0) we have f^′ (λ)=−∫ ((3λ^2 )/((x^3 −λ^3 )^2 )) dx ⇒∫ (dx/(x^3 −λ^3 ))=−(1/(3λ^2 ))f^′ (λ) and ∫ (dx/(x^3 −1)) =−(1/3)f^′ (1) let explicit f(λ)let x=λu ⇒ f(λ)=∫ ((λdu)/(λ^3 (u^3 −1))) =(1/λ^2 )∫ (du/(u^3 −1)) and g(u)=(1/(u^3 −1))=(1/((u−1)(u^2 +u+1)))=(a/(u−1))+((bu+c)/(u^2 +u+1)) a=(1/3) ,lim_(u→+∞) uG(u)=0=a+b ⇒b=−(1/3) g(o)=−1=−a+c ⇒c=−1+a=−1+(1/3)=−(2/3) ⇒ g(u)=(1/(3(u−1)))+((−(1/3)u−(2/3))/(u^2 +u+1))=(1/(3(u−1)))−(1/3)×((u+2)/(u^2 +u+1)) =(1/(3(u−1)))−(1/6)×((2u+1+3)/(u^2 +u+1)) ⇒∫ g(u)du=(1/3)ln∣u−1∣ −(1/6)ln(u^2 +u+1)−(1/2)∫ (du/((u+(1/2))^2 +(3/4)))(→u+(1/2)=((√3)/2)z) ⇒ ∫ (du/((u+(1/2))^2 +(3/4))) =((√3)/2)×(4/3)∫ (dz/(z^2 +1))=(2/( (√3)))arctan(((2u+1)/( (√3)))) ⇒ ∫ g(u)du =(1/3)ln∣u−1∣−(1/6)ln(u^2 +u+1)−(1/( (√3))) arctan(((2u+1)/( (√3))))+c f(λ)=(1/λ^2 ){ (1/3)ln∣(x/λ)−1∣−(1/6)ln((x^2 /λ^2 )+(x/λ)+1)−(1/( (√3)))arctan(((((2x)/λ)+1)/( (√3))))+c ⇒ now its eazy to calculate f^′ (λ) and f^′ (1)...be continued...

$$\mathrm{A}\:=\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{2}} }\:\:\mathrm{let}\:\mathrm{f}\left(\lambda\right)=\int\:\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{3}} −\lambda^{\mathrm{3}} }\:\:\:\left(\lambda>\mathrm{0}\right)\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{f}^{'} \left(\lambda\right)=−\int\:\:\frac{\mathrm{3}\lambda^{\mathrm{2}} }{\left(\mathrm{x}^{\mathrm{3}} −\lambda^{\mathrm{3}} \right)^{\mathrm{2}} }\:\mathrm{dx}\:\Rightarrow\int\:\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{3}} −\lambda^{\mathrm{3}} }=−\frac{\mathrm{1}}{\mathrm{3}\lambda^{\mathrm{2}} }\mathrm{f}^{'} \left(\lambda\right)\:\mathrm{and} \\ $$$$\int\:\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{3}} −\mathrm{1}}\:=−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{f}^{'} \left(\mathrm{1}\right)\:\:\mathrm{let}\:\mathrm{explicit}\:\mathrm{f}\left(\lambda\right)\mathrm{let}\:\mathrm{x}=\lambda\mathrm{u}\:\Rightarrow \\ $$$$\mathrm{f}\left(\lambda\right)=\int\:\:\frac{\lambda\mathrm{du}}{\lambda^{\mathrm{3}} \left(\mathrm{u}^{\mathrm{3}} −\mathrm{1}\right)}\:=\frac{\mathrm{1}}{\lambda^{\mathrm{2}} }\int\:\:\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{3}} −\mathrm{1}}\:\mathrm{and} \\ $$$$\mathrm{g}\left(\mathrm{u}\right)=\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{3}} −\mathrm{1}}=\frac{\mathrm{1}}{\left(\mathrm{u}−\mathrm{1}\right)\left(\mathrm{u}^{\mathrm{2}} \:+\mathrm{u}+\mathrm{1}\right)}=\frac{\mathrm{a}}{\mathrm{u}−\mathrm{1}}+\frac{\mathrm{bu}+\mathrm{c}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{u}+\mathrm{1}} \\ $$$$\mathrm{a}=\frac{\mathrm{1}}{\mathrm{3}}\:,\mathrm{lim}_{\mathrm{u}\rightarrow+\infty} \mathrm{uG}\left(\mathrm{u}\right)=\mathrm{0}=\mathrm{a}+\mathrm{b}\:\Rightarrow\mathrm{b}=−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{g}\left(\mathrm{o}\right)=−\mathrm{1}=−\mathrm{a}+\mathrm{c}\:\Rightarrow\mathrm{c}=−\mathrm{1}+\mathrm{a}=−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}=−\frac{\mathrm{2}}{\mathrm{3}}\:\Rightarrow \\ $$$$\mathrm{g}\left(\mathrm{u}\right)=\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{u}−\mathrm{1}\right)}+\frac{−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{u}−\frac{\mathrm{2}}{\mathrm{3}}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{u}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{u}−\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{u}+\mathrm{2}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{u}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{u}−\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{6}}×\frac{\mathrm{2u}+\mathrm{1}+\mathrm{3}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{u}+\mathrm{1}}\:\Rightarrow\int\:\mathrm{g}\left(\mathrm{u}\right)\mathrm{du}=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\mid\mathrm{u}−\mathrm{1}\mid \\ $$$$−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\left(\mathrm{u}^{\mathrm{2}} \:+\mathrm{u}+\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{\mathrm{du}}{\left(\mathrm{u}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}\left(\rightarrow\mathrm{u}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{z}\right)\:\Rightarrow \\ $$$$\int\:\:\frac{\mathrm{du}}{\left(\mathrm{u}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}}\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}×\frac{\mathrm{4}}{\mathrm{3}}\int\:\frac{\mathrm{dz}}{\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\mathrm{arctan}\left(\frac{\mathrm{2u}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\:\Rightarrow \\ $$$$\int\:\mathrm{g}\left(\mathrm{u}\right)\mathrm{du}\:=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\mid\mathrm{u}−\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\left(\mathrm{u}^{\mathrm{2}} \:+\mathrm{u}+\mathrm{1}\right)−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:\mathrm{arctan}\left(\frac{\mathrm{2u}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+\mathrm{c} \\ $$$$\mathrm{f}\left(\lambda\right)=\frac{\mathrm{1}}{\lambda^{\mathrm{2}} }\left\{\:\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\mid\frac{\mathrm{x}}{\lambda}−\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\left(\frac{\mathrm{x}^{\mathrm{2}} }{\lambda^{\mathrm{2}} }+\frac{\mathrm{x}}{\lambda}+\mathrm{1}\right)−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{arctan}\left(\frac{\frac{\mathrm{2x}}{\lambda}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+\mathrm{c}\:\Rightarrow\right. \\ $$$$\mathrm{now}\:\mathrm{its}\:\mathrm{eazy}\:\mathrm{to}\:\mathrm{calculate}\:\mathrm{f}^{'} \left(\lambda\right)\:\mathrm{and}\:\mathrm{f}^{'} \left(\mathrm{1}\right)...\mathrm{be}\:\mathrm{continued}... \\ $$$$ \\ $$

Commented by mathmax by abdo last updated on 08/Dec/20

∫ (dx/((x^3 −λ^3 )^2 ))=−(1/(3λ^2 ))f^′ (λ) ⇒∫ (dx/((x^3 −1)^2 ))=−(1/3)f^′ (1) (eror of typo)

$$\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{3}} −\lambda^{\mathrm{3}} \right)^{\mathrm{2}} }=−\frac{\mathrm{1}}{\mathrm{3}\lambda^{\mathrm{2}} }\mathrm{f}^{'} \left(\lambda\right)\:\Rightarrow\int\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{2}} }=−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{f}^{'} \left(\mathrm{1}\right) \\ $$$$\left(\mathrm{eror}\:\mathrm{of}\:\mathrm{typo}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com