... ◂advanced calculus▶... prove that ::: Ω=∫_0 ^( 1) {((cos(log(x))−1)/(log(x)))}dx=((log(2))/2) ...∗adopted from youtube∗... ∗ ∗ youtube solution is not considered ∗ ∗


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 125133 by mnjuly1970 last updated on 08/Dec/20
$... ◂advanced calculus▶... prove that ::: Ω=∫_0 ^( 1) {((cos(log(x))−1)/(log(x)))}dx=((log(2))/2) ...∗adopted from youtube∗... ∗ ∗ youtube solution is not considered ∗ ∗$
$. . . ◂ a d v a n c e d c a l c u l u s ▸ . . .$ $p r o v e t h a t :::$ $Ω = \int_{0}^{1} {\frac{c o s (l o g (x)) - 1}{l o g (x)}} d x = \frac{l o g (2)}{2}$ $. . . * a d o p t e d f r o m y o u t u b e * . . .$ $* * y o u t u b e s o l u t i o n i s n o t c o n s i d e r e d * *$
	Answered by mathmax by abdo last updated on 08/Dec/20
	$I=∫_0 ^1 ((cos(logx)−1)/(logx)) we do the chamgement logx=−t ⇒x=e^(−t) I=∫_∞ ^0 ((cost−1)/(−t))(−e^(−t) )dt =−∫_0 ^∞ ((cost−1)/t)e^(−t) dt let f(a) =∫_0 ^∞ ((cost−1)/t)e^(−at) dt with a>0 we have f^′ (a)=−∫_0 ^∞ (cost−1)e^(−at) dt =−∫_0 ^∞ e^(−at) cost +∫_0 ^∞ e^(−at) dt but ∫_0 ^∞ e^(−at) dt =[−(1/a)e^(−at) ]_0 ^∞ =(1/a) ∫_0 ^∞ e^(−at) cost dt =Re(∫_0 ^∞ e^(−at+it) dt) snd ∫_0 ^∞ e^((−a+i)t) dt =[(1/(−a+i))e^((−a+i)t) ]_0 ^∞ =((−1)/(a−i)){−1} =(1/(a−i))=((a+i)/(a^2 +1)) ⇒∫_0 ^∞ e^(−at) cost dt =(a/(a^2 +1)) ⇒f^′ (a)=−(a/(1+a^2 ))+(1/a) ⇒ f(a)=lna−(1/2)ln(1+a^2 )+C =ln((a/( (√(a^2 +1))))) +c ∣f(a)∣≤(m/a)→0 (a→+∞) ⇒c=0 ⇒f(a)=ln((a/( (√(1+a^2 ))))) I =−f(1)=−ln((1/( (√2))))=ln((√2))=((ln(2))/2)$
	$I = \int_{0}^{1} \frac{\cos (logx) - 1}{logx} we do the chamgement logx = - t \Rightarrow x = e^{- t}$ $I = \int_{\infty}^{0} \frac{cost - 1}{- t} (- e^{- t}) dt = - \int_{0}^{\infty} \frac{cost - 1}{t} e^{- t} dt$ $let f (a) = \int_{0}^{\infty} \frac{cost - 1}{t} e^{- at} dt with a > 0 we have$ $f^{^{'}} (a) = - \int_{0}^{\infty} (cost - 1) e^{- a t} dt = - \int_{0}^{\infty} e^{- a t} cost + \int_{0}^{\infty} e^{- a t} dt$ $but \int_{0}^{\infty} e^{- a t} dt = {[- \frac{1}{a} e^{- a t}]}_{0}^{\infty} = \frac{1}{a}$ $\int_{0}^{\infty} e^{- a t} cost dt = Re (\int_{0}^{\infty} e^{- a t + it} dt) snd$ $\int_{0}^{\infty} e^{(- a + i) t} dt = {[\frac{1}{- a + i} e^{(- a + i) t}]}_{0}^{\infty} = \frac{- 1}{a - i} {- 1} = \frac{1}{a - i} = \frac{a + i}{a^{2} + 1}$ $\Rightarrow \int_{0}^{\infty} e^{- at} cost dt = \frac{a}{a^{2} + 1} \Rightarrow f^{^{'}} (a) = - \frac{a}{1 + a^{2}} + \frac{1}{a} \Rightarrow$ $f (a) = lna - \frac{1}{2} \ln (1 + a^{2}) + C = \ln (\frac{a}{\sqrt{a^{2} + 1}}) + c$ $∣ f (a) ∣⩽ \frac{m}{a} \to 0 (a \to + \infty) \Rightarrow c = 0 \Rightarrow f (a) = \ln (\frac{a}{\sqrt{1 + a^{2}}})$ $I = - f (1) = - \ln (\frac{1}{\sqrt{2}}) = \ln (\sqrt{2}) = \frac{\ln (2)}{2}$
	Commented by mnjuly1970 last updated on 08/Dec/20

	$t h a n k y o u s o m u c h$ $m r m a x . g r a t e f u l . . . .$
	Commented by mathmax by abdo last updated on 08/Dec/20

	$you are welcome sir$
	Answered by Dwaipayan Shikari last updated on 08/Dec/20

	$\int_{0}^{1} \frac{c o s (l o g x) - 1}{l o g x} d x$ $= \int_{- \infty}^{0} e^{t} \frac{c o s (t) - 1}{t} d t l o g x = t \Rightarrow \frac{1}{x} = \frac{d t}{d x}$ $I (a) = 2 \int_{0}^{\infty} \frac{c o s t - 1}{t} e^{- a t} d t$ $I^{'} (a) = - \int_{0}^{\infty} {c o s t e}^{- a t} + \int_{0}^{\infty} e^{- a t} d t$ $= - \frac{1}{2} \int_{0}^{\infty} e^{- t (a - i)} + e^{- t (i + a)} d t + \frac{1}{a}$ $= - \frac{1}{2} (\frac{1}{a - i} + \frac{1}{i + a}) + \frac{1}{a} = - \frac{a}{a^{2} + 1} + \frac{1}{a}$ $I (a) = - \frac{1}{2} l o g (a^{2} + 1) + l o g (a) + C$ $a \to \infty C = 0$ $I (1) = \frac{1}{2} l o g (2)$
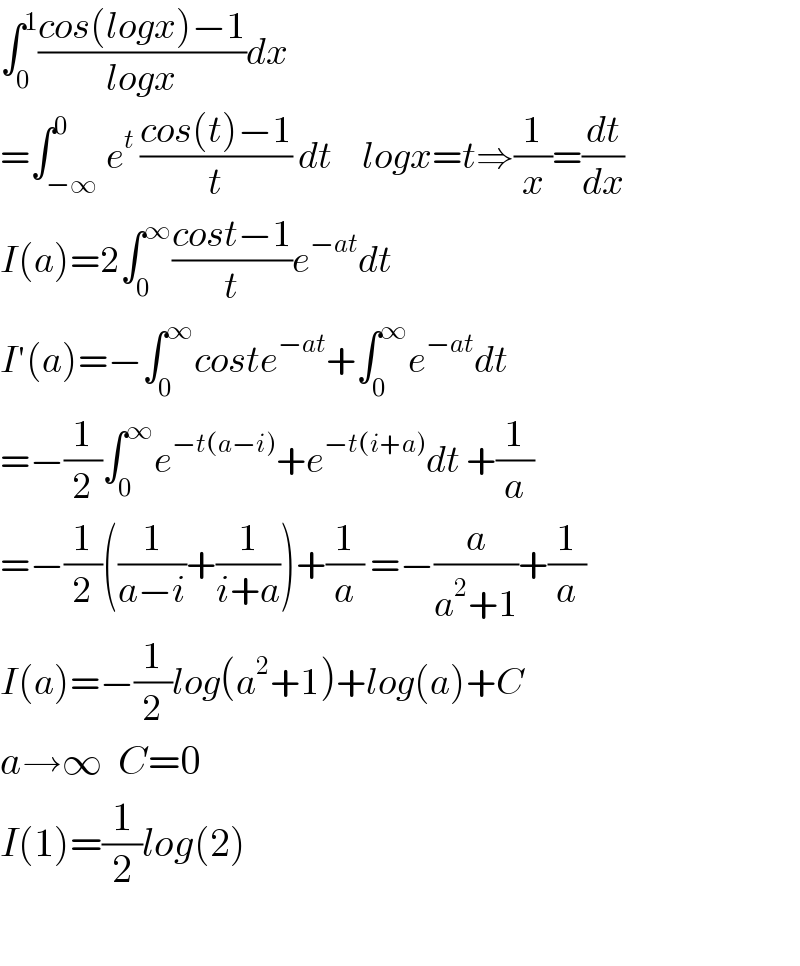
	Commented by mnjuly1970 last updated on 08/Dec/20

	$b r a v o m r p a y a n . t h a n k y o u$ $s o m u c h . .$
	Answered by mnjuly1970 last updated on 08/Dec/20

	$s o l u t i o n :$ $Ω = R e (\int_{0}^{1} \frac{x^{i} - 1}{l o g (x)} d x) = R e (l n (1 + i))$ $= R e (l n (\sqrt{2} e^{\frac{i π}{4}})) = R e [l n (\sqrt{2}) + i \frac{π}{4}]$ $∴ Ω = \frac{l n (2)}{2} ✓$
	Commented by mathmax by abdo last updated on 08/Dec/20

	$you are taking route 66 in america . .!$
	Commented by mnjuly1970 last updated on 08/Dec/20

	$s i n c e r e l y y o u r s$ $m . n . 1970$
	Commented by mnjuly1970 last updated on 09/Dec/20

	$s i r m a x$ $s i n c e : s o m e i n t e g r a l s a n d p r o b l e m s$ $w e r e s o l v e d m a n y t i m e t h e r e f o r e i t r i e d$ $t o s h o r t e n t h e s o l u t i o n .$ $e x a m p l e :$ $l n (a + 1) = \int_{0}^{1} (\frac{x^{a} - 1}{l n (x)}) d x, . . . .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum