Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 125297 by mnjuly1970 last updated on 09/Dec/20

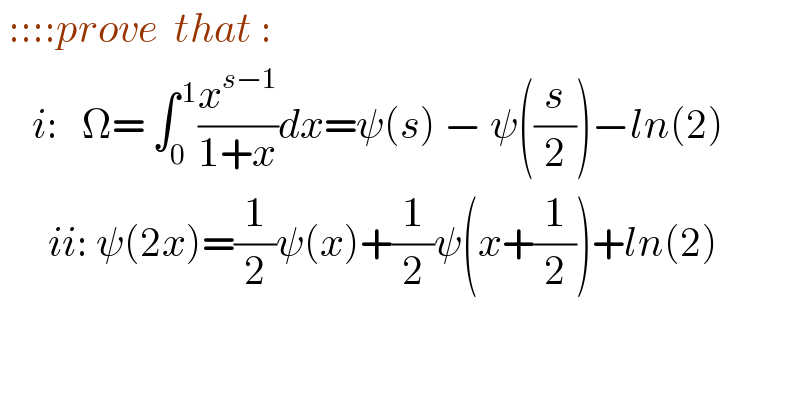
::::prove that : i: Ω= ∫_0 ^( 1) (x^(s−1) /(1+x))dx=ψ(s) − ψ((s/2))−ln(2) ii: ψ(2x)=(1/2)ψ(x)+(1/2)ψ(x+(1/2))+ln(2)

$$\:::::{prove}\:\:{that}\:: \\ $$$$\:\:\:\:{i}:\:\:\:\Omega=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{x}^{{s}−\mathrm{1}} }{\mathrm{1}+{x}}{dx}=\psi\left({s}\right)\:−\:\psi\left(\frac{{s}}{\mathrm{2}}\right)−{ln}\left(\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:{ii}:\:\psi\left(\mathrm{2}{x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\psi\left({x}\right)+\frac{\mathrm{1}}{\mathrm{2}}\psi\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)+{ln}\left(\mathrm{2}\right) \\ $$

Answered by Bird last updated on 09/Dec/20

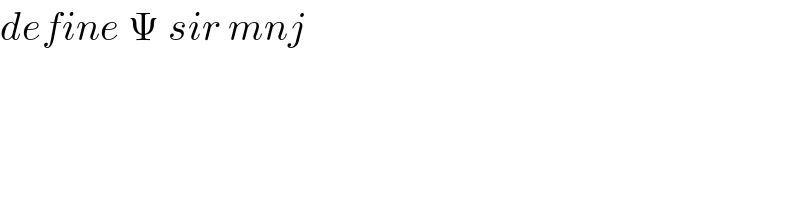
define Ψ sir mnj

$${define}\:\Psi\:{sir}\:{mnj} \\ $$

Commented by hatakekakashi1729gmailcom last updated on 10/Dec/20

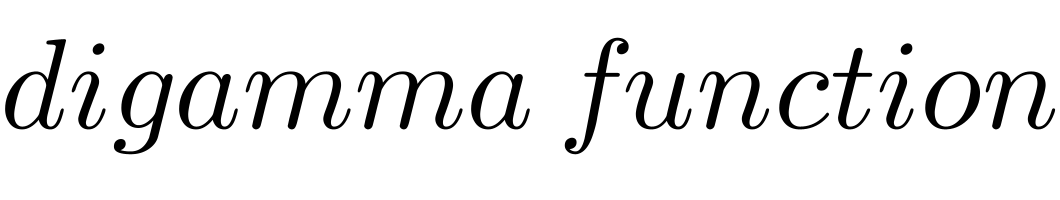
digamma function

$${digamma}\:{function} \\ $$

Commented by mnjuly1970 last updated on 10/Dec/20

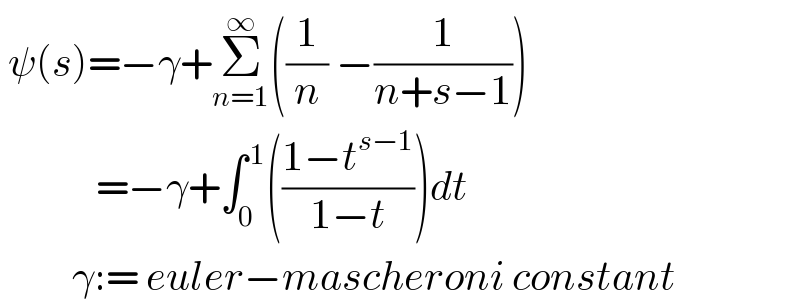
ψ(s)=−γ+Σ_(n=1) ^∞ ((1/n) −(1/(n+s−1))) =−γ+∫_0 ^( 1) (((1−t^(s−1) )/(1−t)))dt γ:= euler−mascheroni constant

$$\:\psi\left({s}\right)=−\gamma+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}}\:−\frac{\mathrm{1}}{{n}+{s}−\mathrm{1}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=−\gamma+\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\frac{\mathrm{1}−{t}^{{s}−\mathrm{1}} }{\mathrm{1}−{t}}\right){dt} \\ $$$$\:\:\:\:\:\:\:\:\:\gamma:=\:{euler}−{mascheroni}\:{constant} \\ $$

Commented by mnjuly1970 last updated on 10/Dec/20

thank you sir..

$${thank}\:{you}\:{sir}.. \\ $$

Answered by Dwaipayan Shikari last updated on 10/Dec/20

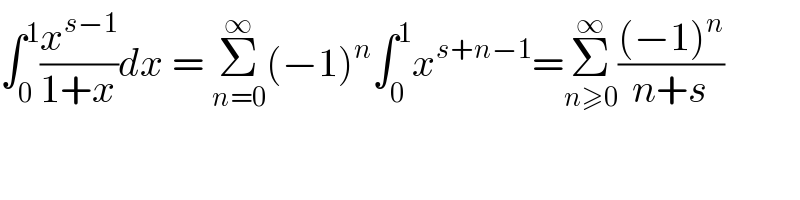
∫_0 ^1 (x^(s−1) /(1+x))dx = Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 x^(s+n−1) =Σ_(n≥0) ^∞ (((−1)^n )/(n+s))

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{s}−\mathrm{1}} }{\mathrm{1}+{x}}{dx}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{s}+{n}−\mathrm{1}} =\underset{{n}\geqslant\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+{s}} \\ $$

Answered by mindispower last updated on 11/Dec/20

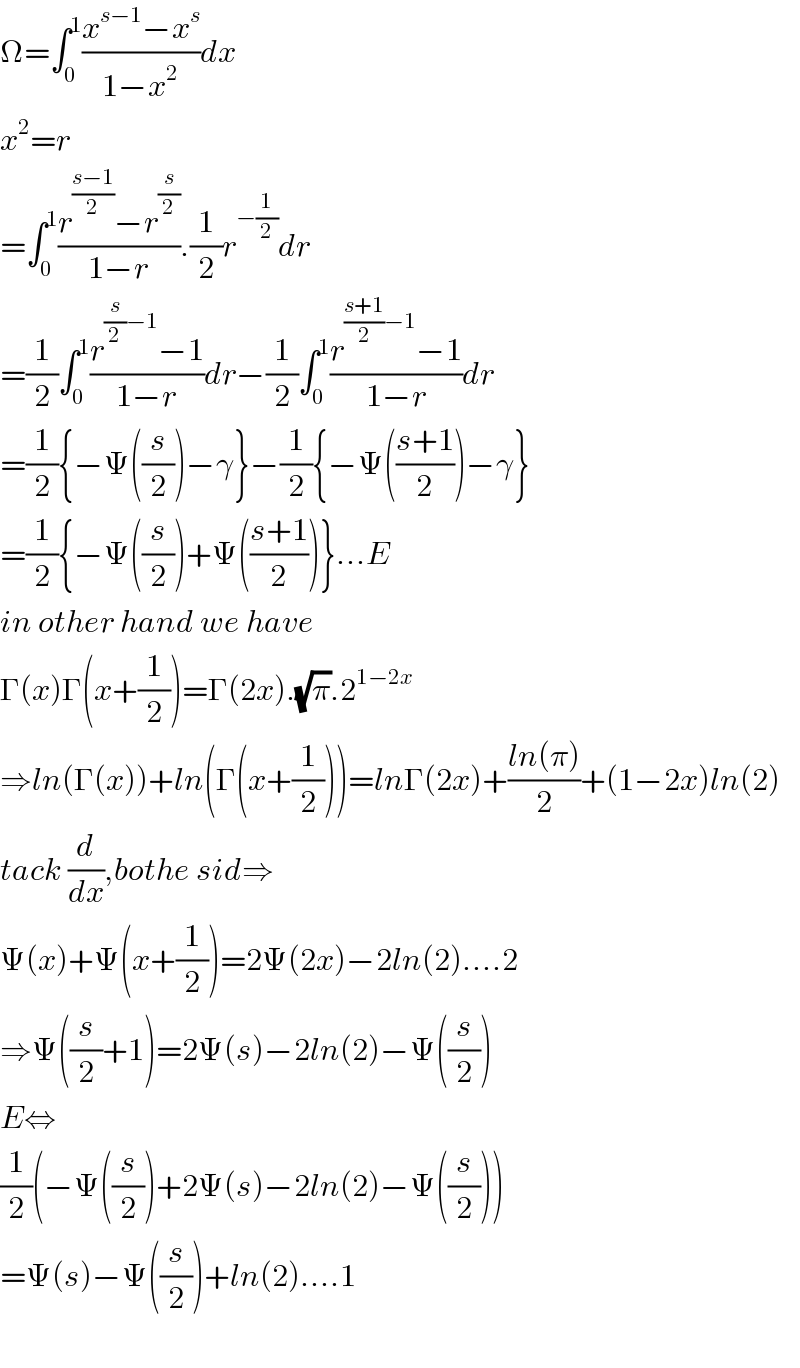
Ω=∫_0 ^1 ((x^(s−1) −x^s )/(1−x^2 ))dx x^2 =r =∫_0 ^1 ((r^((s−1)/2) −r^(s/2) )/(1−r)).(1/2)r^(−(1/2)) dr =(1/2)∫_0 ^1 ((r^((s/2)−1) −1)/(1−r))dr−(1/2)∫_0 ^1 ((r^(((s+1)/2)−1) −1)/(1−r))dr =(1/2){−Ψ((s/2))−γ}−(1/2){−Ψ(((s+1)/2))−γ} =(1/2){−Ψ((s/2))+Ψ(((s+1)/2))}...E in other hand we have Γ(x)Γ(x+(1/2))=Γ(2x).(√π).2^(1−2x) ⇒ln(Γ(x))+ln(Γ(x+(1/2)))=lnΓ(2x)+((ln(π))/2)+(1−2x)ln(2) tack (d/dx),bothe sid⇒ Ψ(x)+Ψ(x+(1/2))=2Ψ(2x)−2ln(2)....2 ⇒Ψ((s/2)+1)=2Ψ(s)−2ln(2)−Ψ((s/2)) E⇔ (1/2)(−Ψ((s/2))+2Ψ(s)−2ln(2)−Ψ((s/2))) =Ψ(s)−Ψ((s/2))+ln(2)....1

$$\Omega=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{s}−\mathrm{1}} −{x}^{{s}} }{\mathrm{1}−{x}^{\mathrm{2}} }{dx} \\ $$$${x}^{\mathrm{2}} ={r} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{r}^{\frac{{s}−\mathrm{1}}{\mathrm{2}}} −{r}^{\frac{{s}}{\mathrm{2}}} }{\mathrm{1}−{r}}.\frac{\mathrm{1}}{\mathrm{2}}{r}^{−\frac{\mathrm{1}}{\mathrm{2}}} {dr} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{r}^{\frac{{s}}{\mathrm{2}}−\mathrm{1}} −\mathrm{1}}{\mathrm{1}−{r}}{dr}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{r}^{\frac{{s}+\mathrm{1}}{\mathrm{2}}−\mathrm{1}} −\mathrm{1}}{\mathrm{1}−{r}}{dr} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{−\Psi\left(\frac{{s}}{\mathrm{2}}\right)−\gamma\right\}−\frac{\mathrm{1}}{\mathrm{2}}\left\{−\Psi\left(\frac{{s}+\mathrm{1}}{\mathrm{2}}\right)−\gamma\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{−\Psi\left(\frac{{s}}{\mathrm{2}}\right)+\Psi\left(\frac{{s}+\mathrm{1}}{\mathrm{2}}\right)\right\}...{E} \\ $$$${in}\:{other}\:{hand}\:{we}\:{have} \\ $$$$\Gamma\left({x}\right)\Gamma\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\Gamma\left(\mathrm{2}{x}\right).\sqrt{\pi}.\mathrm{2}^{\mathrm{1}−\mathrm{2}{x}} \\ $$$$\Rightarrow{ln}\left(\Gamma\left({x}\right)\right)+{ln}\left(\Gamma\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)\right)={ln}\Gamma\left(\mathrm{2}{x}\right)+\frac{{ln}\left(\pi\right)}{\mathrm{2}}+\left(\mathrm{1}−\mathrm{2}{x}\right){ln}\left(\mathrm{2}\right) \\ $$$${tack}\:\frac{{d}}{{dx}},{bothe}\:{sid}\Rightarrow \\ $$$$\Psi\left({x}\right)+\Psi\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{2}\Psi\left(\mathrm{2}{x}\right)−\mathrm{2}{ln}\left(\mathrm{2}\right)....\mathrm{2} \\ $$$$\Rightarrow\Psi\left(\frac{{s}}{\mathrm{2}}+\mathrm{1}\right)=\mathrm{2}\Psi\left({s}\right)−\mathrm{2}{ln}\left(\mathrm{2}\right)−\Psi\left(\frac{{s}}{\mathrm{2}}\right) \\ $$$${E}\Leftrightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(−\Psi\left(\frac{{s}}{\mathrm{2}}\right)+\mathrm{2}\Psi\left({s}\right)−\mathrm{2}{ln}\left(\mathrm{2}\right)−\Psi\left(\frac{{s}}{\mathrm{2}}\right)\right) \\ $$$$=\Psi\left({s}\right)−\Psi\left(\frac{{s}}{\mathrm{2}}\right)+{ln}\left(\mathrm{2}\right)....\mathrm{1} \\ $$$$ \\ $$

Commented by mnjuly1970 last updated on 12/Dec/20

mercey sir..

$${mercey}\:{sir}.. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com