
Question and Answers Forum
Question Number 12535 by tawa last updated on 24/Apr/17
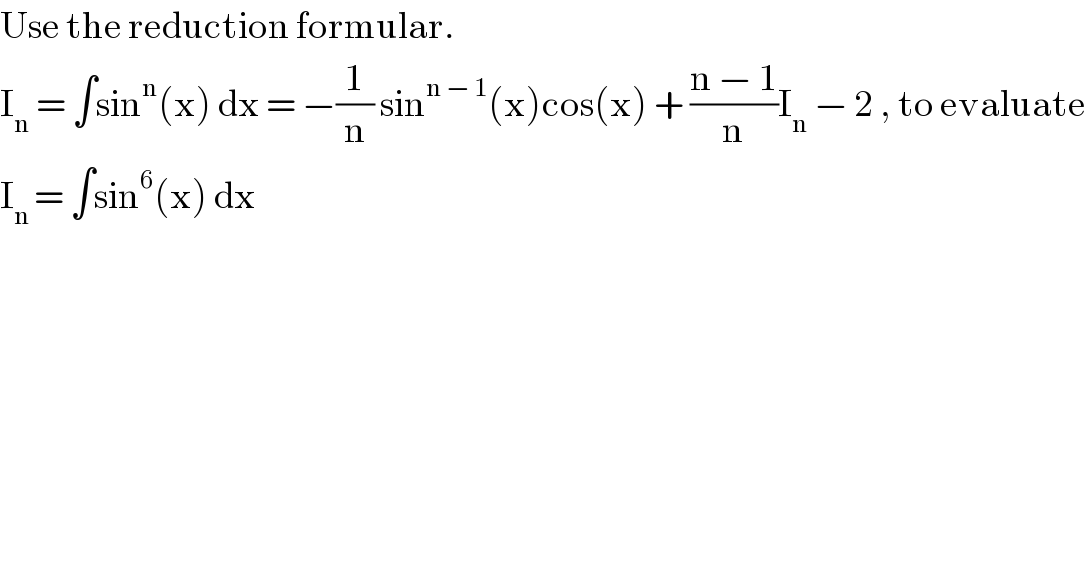
Answered by mrW1 last updated on 25/Apr/17
![I_n = ∫sin^n (x) dx = −(1/n) sin^(n − 1) (x)cos(x) + ((n − 1)/n)I_(n−2) I_6 =∫sin^6 x dx=−(1/6)sin^5 x cos x+(5/6)∫sin^4 x dx I_4 =∫sin^4 x dx=−(1/4)sin^3 x cos x+(3/4)∫sin^2 x dx I_2 =∫sin^2 x dx=−(1/2)sin x cos x+(1/2)∫ dx=(1/2)x−((sin 2x)/4) I_4 =−(1/4)sin^3 x cos x+(3/4)((1/2)x−((sin 2x)/4))=(3/8)x−(3/(16))sin 2x−(1/4)sin^3 cos x I_6 =−(1/6)sin^5 x cos x+(5/6)[(3/8)x−(3/(16))sin 2x−(1/4)sin^3 cos x] =(5/(16))x−(5/(32))sin 2x−(1/(24))sin^3 cos x−(1/6)sin^5 x cos x+C](Q12570.png)
Commented by tawa last updated on 25/Apr/17

| ||
Question and Answers Forum | ||
Question Number 12535 by tawa last updated on 24/Apr/17 | ||
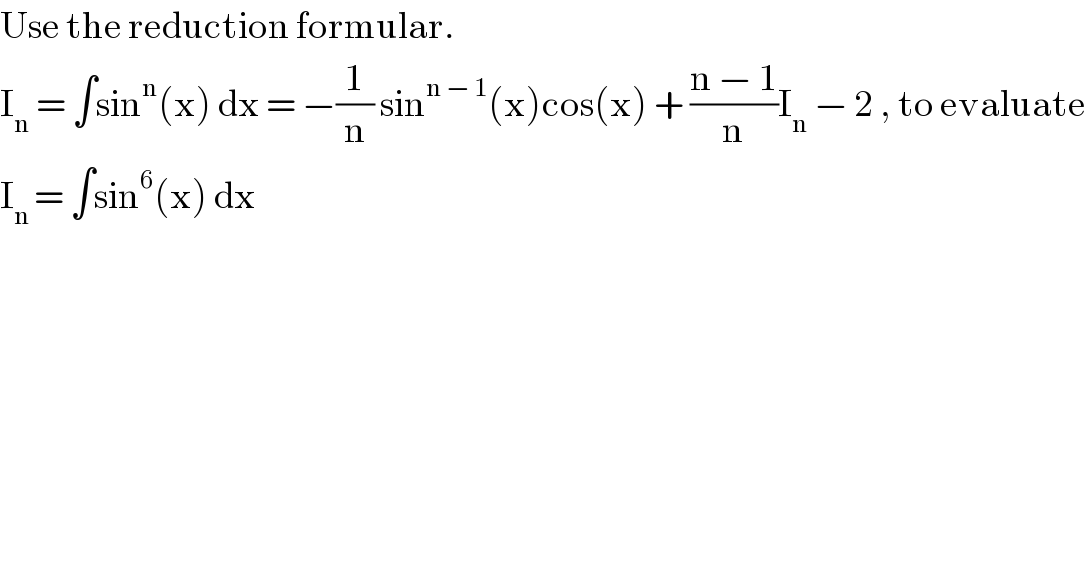 | ||
Answered by mrW1 last updated on 25/Apr/17 | ||
![I_n = ∫sin^n (x) dx = −(1/n) sin^(n − 1) (x)cos(x) + ((n − 1)/n)I_(n−2) I_6 =∫sin^6 x dx=−(1/6)sin^5 x cos x+(5/6)∫sin^4 x dx I_4 =∫sin^4 x dx=−(1/4)sin^3 x cos x+(3/4)∫sin^2 x dx I_2 =∫sin^2 x dx=−(1/2)sin x cos x+(1/2)∫ dx=(1/2)x−((sin 2x)/4) I_4 =−(1/4)sin^3 x cos x+(3/4)((1/2)x−((sin 2x)/4))=(3/8)x−(3/(16))sin 2x−(1/4)sin^3 cos x I_6 =−(1/6)sin^5 x cos x+(5/6)[(3/8)x−(3/(16))sin 2x−(1/4)sin^3 cos x] =(5/(16))x−(5/(32))sin 2x−(1/(24))sin^3 cos x−(1/6)sin^5 x cos x+C](Q12570.png) | ||
| ||
Commented by tawa last updated on 25/Apr/17 | ||
 | ||