{ ((x + y = ((5π)/3))),((sin x = 2sin y)) :}


Question and Answers Forum

All Questions Topic List
None Questions
Previous in All Question Next in All Question
Previous in None Next in None
Question Number 125359 by weltr last updated on 10/Dec/20

${\begin{cases} x + y = \frac{5 π}{3} \\ s i n x = 2 s i n y \end{cases}$
	Answered by Ar Brandon last updated on 10/Dec/20
	${ ((x+y=((5π)/3)),(...(i))),((sinx=2siny),(...(ii))) :} From (i), x+y=((5π)/3) ⇒ y=((5π)/3)−x substituting the above result in (ii) we have ; sinx=2sin(((5π)/3)−x)=2sin(π+(((2π)/3)−x))=2sin(x−((2π)/3)) {sin(π+x)=−sinx=sin(−x)} =2[sin(x)cos(((2π)/3))−cos(x)sin(((2π)/3))] =2[−(1/2)sinx−((√3)/2)cosx]=−sinx−(√3)cosx ⇒2sinx=−(√3)cosx ⇒ tanx=−((√3)/2) x=tan^(−1) (−((√3)/2)) , y=((5π)/3)−tan^(−1) (−((√3)/2))$
	${\begin{cases} x + y = \frac{5 π}{3} & . . . (i) \\ sinx = 2 siny & . . . (ii) \end{cases}$ $From (i), x + y = \frac{5 π}{3} \Rightarrow y = \frac{5 π}{3} - x$ $substituting the above result in (ii) we have;$ $sinx = 2 \sin (\frac{5 π}{3} - x) = 2 \sin (π + (\frac{2 π}{3} - x)) = 2 \sin (x - \frac{2 π}{3})$ ${s i n (π + x) = - s i n x = s i n (- x)}$ $= 2 [\sin (x) \cos (\frac{2 π}{3}) - \cos (x) \sin (\frac{2 π}{3})]$ $= 2 [- \frac{1}{2} sinx - \frac{\sqrt{3}}{2} cosx] = - sinx - \sqrt{3} cosx$ $\Rightarrow 2 sinx = - \sqrt{3} cosx \Rightarrow tanx = - \frac{\sqrt{3}}{2}$ $x = \tan^{- 1} (- \frac{\sqrt{3}}{2}), y = \frac{5 π}{3} - \tan^{- 1} (- \frac{\sqrt{3}}{2})$
	Commented by MJS_new last updated on 10/Dec/20

	$good path but you embezzle at least (10^{1000})!$ $solutions . . .$ $x = n π - \arctan \frac{\sqrt{3}}{2}$ $y = - n π + \frac{5 π}{3} + \arctan \frac{\sqrt{3}}{2}$
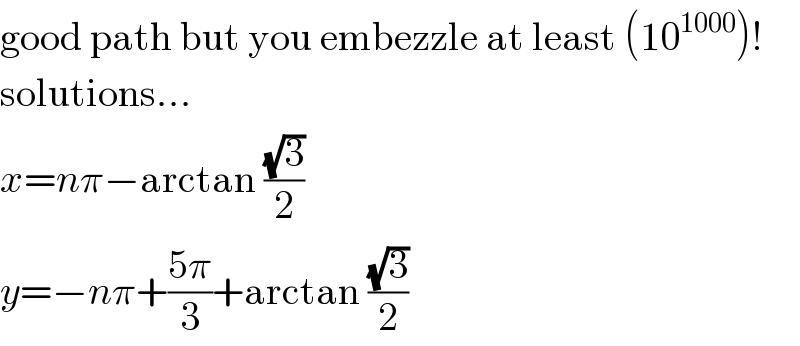
	Commented by Ar Brandon last updated on 10/Dec/20
	��
	Commented by Ar Brandon last updated on 10/Dec/20
	Thanks majesty ��
	Commented by Ar Brandon last updated on 10/Dec/20
	mjs, I meant ��
	Commented by Ar Brandon last updated on 10/Dec/20
	Extend my greetings to her majesty Sir �� Tell her I miss her so much��
	Commented by Dwaipayan Shikari last updated on 10/Dec/20
	you can't tell that you have told
	Commented by Ar Brandon last updated on 10/Dec/20
	tell, told, till��
	Commented by Dwaipayan Shikari last updated on 10/Dec/20
	��
	Commented by Ar Brandon last updated on 10/Dec/20
	��I prefer this��
	Commented by Ar Brandon last updated on 10/Dec/20
	শুভ দিন��
	Commented by Dwaipayan Shikari last updated on 10/Dec/20
	হো
	Answered by Dwaipayan Shikari last updated on 10/Dec/20

	$\frac{s i n x + s i n y}{s i n x - c o s y} = 3 \Rightarrow \frac{t a n (\frac{x + y}{2})}{t a n (\frac{x - y}{2})} = 3 \Rightarrow t a n (\frac{x - y}{2}) = - \frac{1}{3 \sqrt{3}}$ $x - y = 2 k π - {t a n}^{- 1} \frac{1}{3 \sqrt{3}}$ $x = (k + \frac{5}{6}) π - \frac{1}{2} {t a n}^{- 1} \frac{1}{3 \sqrt{3}}, y = (\frac{5}{6} - k) π + \frac{1}{2} {t a n}^{- 1} \frac{1}{3 \sqrt{3}}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum