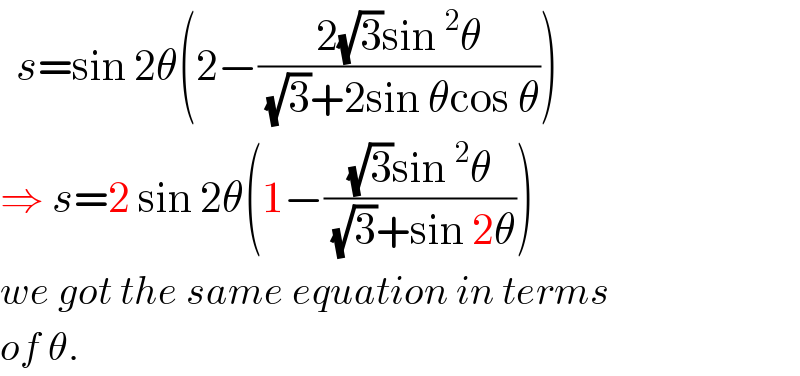Question and Answers Forum

All Questions      Topic List

Mensuration Questions

Previous in All Question      Next in All Question      

Previous in Mensuration      Next in Mensuration      

Question Number 125491 by ajfour last updated on 11/Dec/20

Commented by ajfour last updated on 11/Dec/20

$$Ifoutermosttriangleisequilateral$$$$andradiusofcircleisunity,find$$$$maximumbrownshadedarea.$$

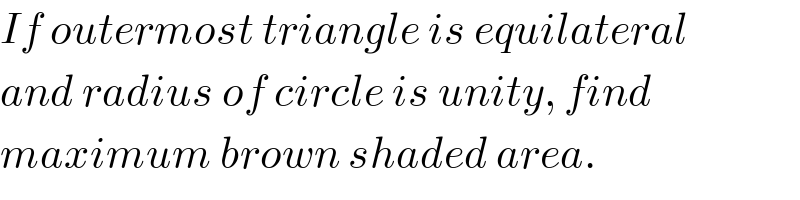
Answered by mr W last updated on 11/Dec/20

Commented by mr W last updated on 11/Dec/20

$$BC=2\cos \theta$$$$AB=\sqrt{7}$$$$\tan \beta =\frac{2{\sin }^2\theta }{\sqrt{3}+2\sin \theta \cos \theta }$$$$DE=\sqrt{3}\tan \beta =\frac{2\sqrt{3}{\sin }^2\theta }{\sqrt{3}+2\sin \theta \cos \theta }$$$$BD=2-\frac{2\sqrt{3}{\sin }^2\theta }{\sqrt{3}+2\sin \theta \cos \theta }$$$$A={\mathrm{\Delta }}_{BCD}=\frac{1}{2}\times 2\cos \theta \times (2-\frac{2\sqrt{3}{\sin }^2\theta }{\sqrt{3}+2\sin \theta \cos \theta })\sin \theta$$$$\Rightarrow A=\sin 2\theta (1-\frac{\sqrt{3}{\sin }^2\theta }{\sqrt{3}+\sin 2\theta })$$$$$$$$A_{max}=0.7393at\theta =35.2354°$$

Commented by ajfour last updated on 11/Dec/20

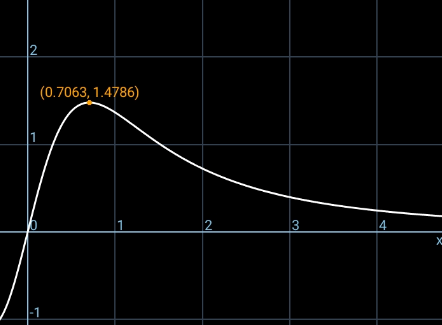
Commented by mr W last updated on 11/Dec/20

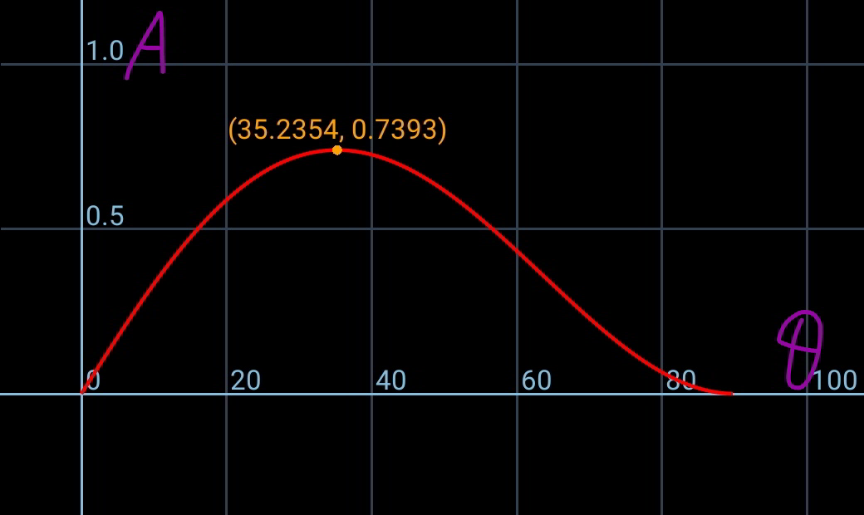
Commented by ajfour last updated on 11/Dec/20

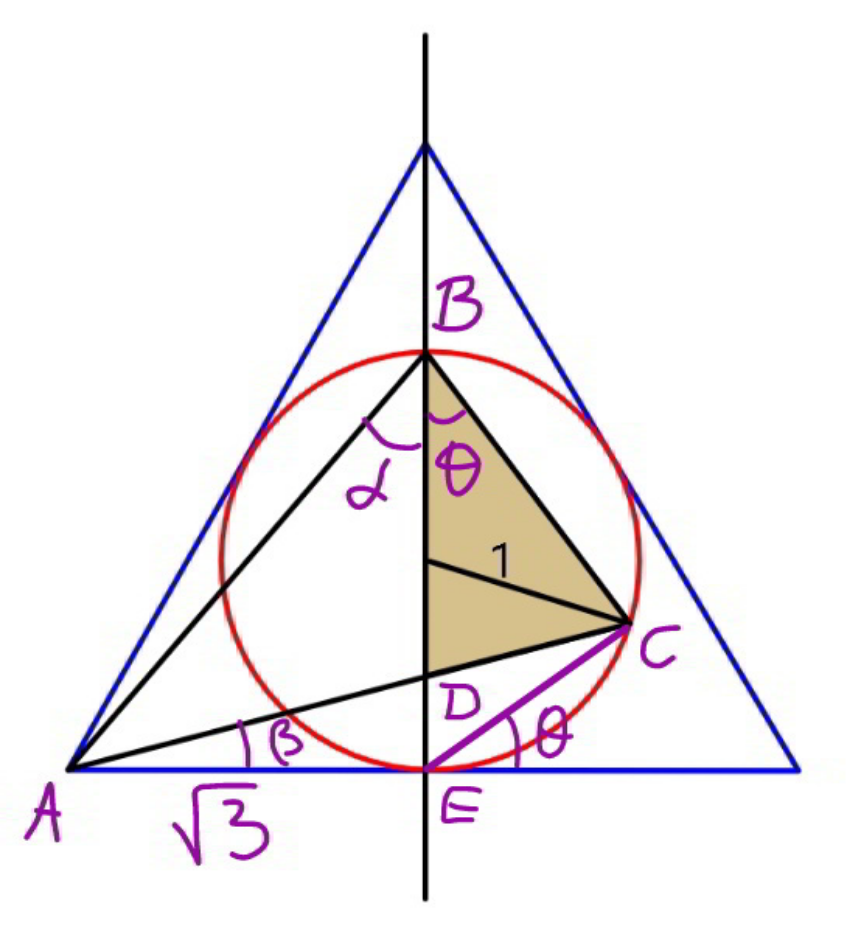
$$\tan \alpha =\frac{\sqrt{3}}{2}$$$$LetbottommostpointofcircleF.$$$$\mathrm{\angle }ADF=\varphi ,centerofcircleO.$$$$letOD=y$$$$\frac{\sin 2\theta }{CD}=\frac{\sin \varphi }{1}=\frac{\sin (\varphi +2\theta )}{y}$$$$\Rightarrow y=\cos 2\theta +\frac{\sin 2\theta }{\tan \varphi }$$$$\tan \varphi =\frac{\sqrt{3}}{1-OD}=\frac{\sqrt{3}}{1-y}$$$$\Rightarrow y=\cos 2\theta +\frac{(1-y)\sin 2\theta }{\sqrt{3}}$$$$\Rightarrow y=\frac{\sqrt{3}\cos 2\theta +\sin 2\theta }{\sqrt{3}+\sin 2\theta }$$$$Areas=2△=(1+y)\sin 2\theta$$$$s=(1+y)\sin 2\theta$$$$=(1+\frac{\sqrt{3}\cos 2\theta +\sin 2\theta }{\sqrt{3}+\sin 2\theta })\sin 2\theta$$$$let\tan \theta =m$$$$s=\sin 2\theta (2-\frac{2\sqrt{3}\sin {}^2\theta }{\sqrt{3}+2\sin \theta \cos \theta })$$$$=\frac{4m}{(1+m^2)}[1-\frac{\sqrt{3}{m}^2}{\sqrt{3}(1+m^2)+2m}]$$$$\Rightarrow {△}_{max}=\frac{s_{max}}{2}\approx 0.7393$$$$\theta \approx {\tan }^{-1}(0.7063)\approx 35.234°$$

Commented by ajfour last updated on 11/Dec/20

$$s=f\left(m\right)$$

Commented by ajfour last updated on 11/Dec/20

$$Excellent,Sir,Thanksalot!$$

Commented by mr W last updated on 12/Dec/20

$$s=\sin 2\theta (2-\frac{2\sqrt{3}\sin {}^2\theta }{\sqrt{3}+2\sin \theta \cos \theta })$$$$\Rightarrow s=2\sin 2\theta (1-\frac{\sqrt{3}\sin {}^2\theta }{\sqrt{3}+\sin 2\theta })$$$$wegotthesameequationinterms$$$$of\theta .$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com