Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 125508 by ajfour last updated on 11/Dec/20

Commented by ajfour last updated on 11/Dec/20

Find R.

$${Find}\:{R}. \\ $$

Answered by ajfour last updated on 11/Dec/20

Commented by ajfour last updated on 11/Dec/20

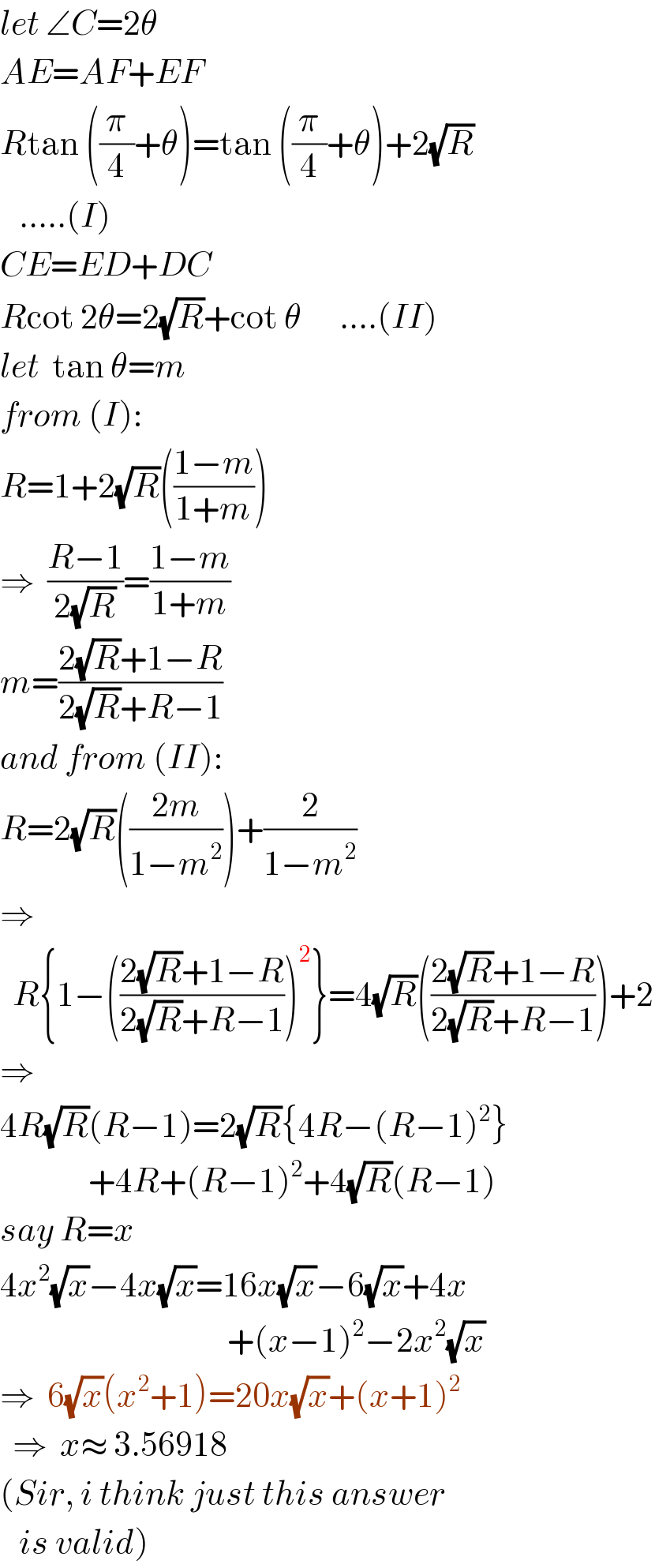
let ∠C=2θ AE=AF+EF Rtan ((π/4)+θ)=tan ((π/4)+θ)+2(√R) .....(I) CE=ED+DC Rcot 2θ=2(√R)+cot θ ....(II) let tan θ=m from (I): R=1+2(√R)(((1−m)/(1+m))) ⇒ ((R−1)/(2(√R)))=((1−m)/(1+m)) m=((2(√R)+1−R)/(2(√R)+R−1)) and from (II): R=2(√R)(((2m)/(1−m^2 )))+(2/(1−m^2 )) ⇒ R{1−(((2(√R)+1−R)/(2(√R)+R−1)))^2 }=4(√R)(((2(√R)+1−R)/(2(√R)+R−1)))+2 ⇒ 4R(√R)(R−1)=2(√R){4R−(R−1)^2 } +4R+(R−1)^2 +4(√R)(R−1) say R=x 4x^2 (√x)−4x(√x)=16x(√x)−6(√x)+4x +(x−1)^2 −2x^2 (√x) ⇒ 6(√x)(x^2 +1)=20x(√x)+(x+1)^2 ⇒ x≈ 3.56918 (Sir, i think just this answer is valid)

$${let}\:\angle{C}=\mathrm{2}\theta \\ $$$${AE}={AF}+{EF} \\ $$$${R}\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}+\theta\right)=\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}+\theta\right)+\mathrm{2}\sqrt{{R}} \\ $$$$\:\:\:.....\left({I}\right) \\ $$$${CE}={ED}+{DC} \\ $$$${R}\mathrm{cot}\:\mathrm{2}\theta=\mathrm{2}\sqrt{{R}}+\mathrm{cot}\:\theta\:\:\:\:\:\:....\left({II}\right) \\ $$$${let}\:\:\mathrm{tan}\:\theta={m} \\ $$$${from}\:\left({I}\right): \\ $$$${R}=\mathrm{1}+\mathrm{2}\sqrt{{R}}\left(\frac{\mathrm{1}−{m}}{\mathrm{1}+{m}}\right) \\ $$$$\Rightarrow\:\:\frac{{R}−\mathrm{1}}{\mathrm{2}\sqrt{{R}}}=\frac{\mathrm{1}−{m}}{\mathrm{1}+{m}} \\ $$$${m}=\frac{\mathrm{2}\sqrt{{R}}+\mathrm{1}−{R}}{\mathrm{2}\sqrt{{R}}+{R}−\mathrm{1}} \\ $$$${and}\:{from}\:\left({II}\right): \\ $$$${R}=\mathrm{2}\sqrt{{R}}\left(\frac{\mathrm{2}{m}}{\mathrm{1}−{m}^{\mathrm{2}} }\right)+\frac{\mathrm{2}}{\mathrm{1}−{m}^{\mathrm{2}} } \\ $$$$\Rightarrow \\ $$$$\:\:{R}\left\{\mathrm{1}−\left(\frac{\mathrm{2}\sqrt{{R}}+\mathrm{1}−{R}}{\mathrm{2}\sqrt{{R}}+{R}−\mathrm{1}}\right)^{\mathrm{2}} \right\}=\mathrm{4}\sqrt{{R}}\left(\frac{\mathrm{2}\sqrt{{R}}+\mathrm{1}−{R}}{\mathrm{2}\sqrt{{R}}+{R}−\mathrm{1}}\right)+\mathrm{2} \\ $$$$\Rightarrow \\ $$$$\mathrm{4}{R}\sqrt{{R}}\left({R}−\mathrm{1}\right)=\mathrm{2}\sqrt{{R}}\left\{\mathrm{4}{R}−\left({R}−\mathrm{1}\right)^{\mathrm{2}} \right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{4}{R}+\left({R}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{4}\sqrt{{R}}\left({R}−\mathrm{1}\right) \\ $$$${say}\:{R}={x} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} \sqrt{{x}}−\mathrm{4}{x}\sqrt{{x}}=\mathrm{16}{x}\sqrt{{x}}−\mathrm{6}\sqrt{{x}}+\mathrm{4}{x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\left({x}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}{x}^{\mathrm{2}} \sqrt{{x}} \\ $$$$\Rightarrow\:\:\mathrm{6}\sqrt{{x}}\left({x}^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{20}{x}\sqrt{{x}}+\left({x}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\:\:\Rightarrow\:\:{x}\approx\:\mathrm{3}.\mathrm{56918} \\ $$$$\left({Sir},\:{i}\:{think}\:{just}\:{this}\:{answer}\right. \\ $$$$\left.\:\:\:{is}\:{valid}\right) \\ $$

Commented by mr W last updated on 11/Dec/20

yes, you are right sir!

$${yes},\:{you}\:{are}\:{right}\:{sir}! \\ $$

Answered by mr W last updated on 11/Dec/20

Commented by mr W last updated on 11/Dec/20

sin α=((R−1)/(R+1)) sin β=(1/(R+1)) γ=α−β=(π/2)−2α ⇒3α=(π/2)+β ⇒sin (3α)=sin ((π/2)+β)=cos β ⇒sin α (3−4 sin^2 α)=cos β ⇒(((R−1)/(R+1)))[3−4×(((R−1)/(R+1)))^2 ]=((√((R+1)^2 −1))/(R+1)) ⇒(R−1)[3−4×(((R−1)/(R+1)))^2 ]=(√(R(R+2))) ⇒R≈2.3981 or 3.5692

$$\mathrm{sin}\:\alpha=\frac{{R}−\mathrm{1}}{{R}+\mathrm{1}} \\ $$$$\mathrm{sin}\:\beta=\frac{\mathrm{1}}{{R}+\mathrm{1}} \\ $$$$\gamma=\alpha−\beta=\frac{\pi}{\mathrm{2}}−\mathrm{2}\alpha \\ $$$$\Rightarrow\mathrm{3}\alpha=\frac{\pi}{\mathrm{2}}+\beta \\ $$$$\Rightarrow\mathrm{sin}\:\left(\mathrm{3}\alpha\right)=\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}+\beta\right)=\mathrm{cos}\:\beta \\ $$$$\Rightarrow\mathrm{sin}\:\alpha\:\left(\mathrm{3}−\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\alpha\right)=\mathrm{cos}\:\beta \\ $$$$\Rightarrow\left(\frac{{R}−\mathrm{1}}{{R}+\mathrm{1}}\right)\left[\mathrm{3}−\mathrm{4}×\left(\frac{{R}−\mathrm{1}}{{R}+\mathrm{1}}\right)^{\mathrm{2}} \right]=\frac{\sqrt{\left({R}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}}}{{R}+\mathrm{1}} \\ $$$$\Rightarrow\left({R}−\mathrm{1}\right)\left[\mathrm{3}−\mathrm{4}×\left(\frac{{R}−\mathrm{1}}{{R}+\mathrm{1}}\right)^{\mathrm{2}} \right]=\sqrt{{R}\left({R}+\mathrm{2}\right)} \\ $$$$\Rightarrow{R}\approx\mathrm{2}.\mathrm{3981}\:{or}\:\mathrm{3}.\mathrm{5692} \\ $$

Commented by ajfour last updated on 11/Dec/20

Thanks Sir, nice way!

$${Thanks}\:{Sir},\:{nice}\:{way}!\: \\ $$

Answered by islom last updated on 11/Feb/21

Terms of Service

Privacy Policy

Contact: info@tinkutara.com