Question and Answers Forum
Question Number 125572 by ajfour last updated on 12/Dec/20
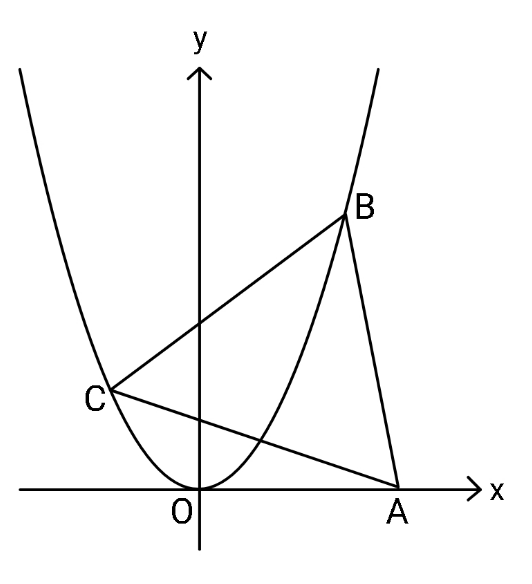
Commented by ajfour last updated on 12/Dec/20
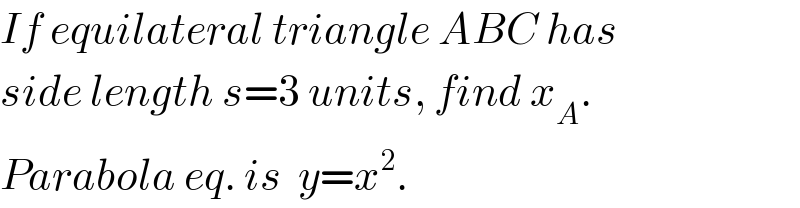
Commented by mr W last updated on 12/Dec/20
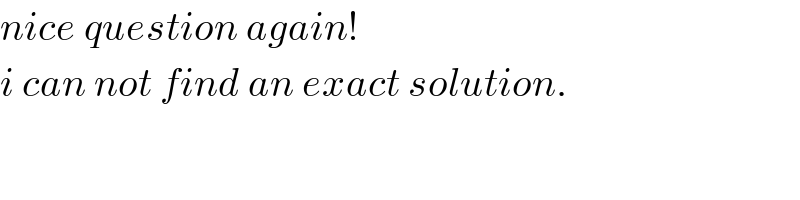
Answered by mr W last updated on 12/Dec/20
![A(a,0) with a≥0 D(h,k) with D=midpoint BC k^2 +(h−a)^2 =((3s^2 )/4) ...(i) eqn. of BC: y=k−((h−a)/k)(x−h)=((a−h)/k)x+k−((h(a−h))/k) intersection x^2 =((a−h)/k)x+k−((h(a−h))/k) x^2 −((a−h)/k)x−k+((h(a−h))/k)=0 x_1 +x_2 =((a−h)/k)=2h ...(ii) x_1 x_2 =−k+((h(a−h))/k) (y_2 −y_1 )^2 +(x_2 −x_1 )^2 =s^2 (x_2 ^2 −x_1 ^2 )^2 +(x_2 −x_1 )^2 =s^2 [(x_2 +x_1 )^2 +1][(x_2 +x_1 )^2 −4x_1 x_2 ]=s^2 4(4h^2 +1)(h^2 +k−((h(a−h))/k))=s^2 ...(iii) from (ii): k=((a−h)/(2h)) ...(I) put (I) into (i): (((a−h)^2 )/(4h^2 ))+(a−h)^2 =((3s^2 )/4) (1+4h^2 )(a−h)^2 =3s^2 h^2 ⇒a=h(1+s(√(3/(1+4h^2 )))) ...(II) put into (iii): ⇒2(1+4h^2 )(s(√(3/(1+4h^2 )))−2h^2 )=s^2 ...(III) for a given s (≤4.73565) we get h from (III) and then a from (II).](Q125582.png)
Commented by mr W last updated on 12/Dec/20
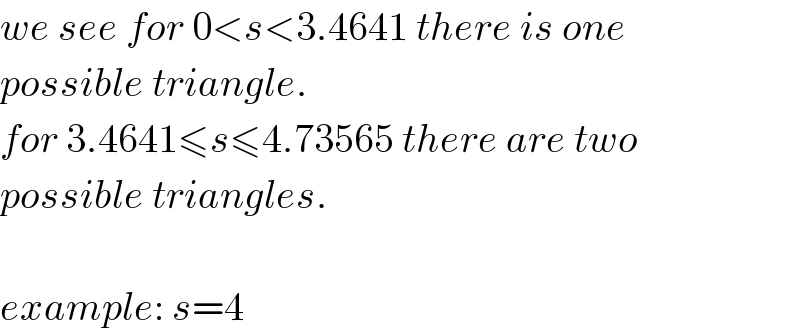
Commented by mr W last updated on 12/Dec/20
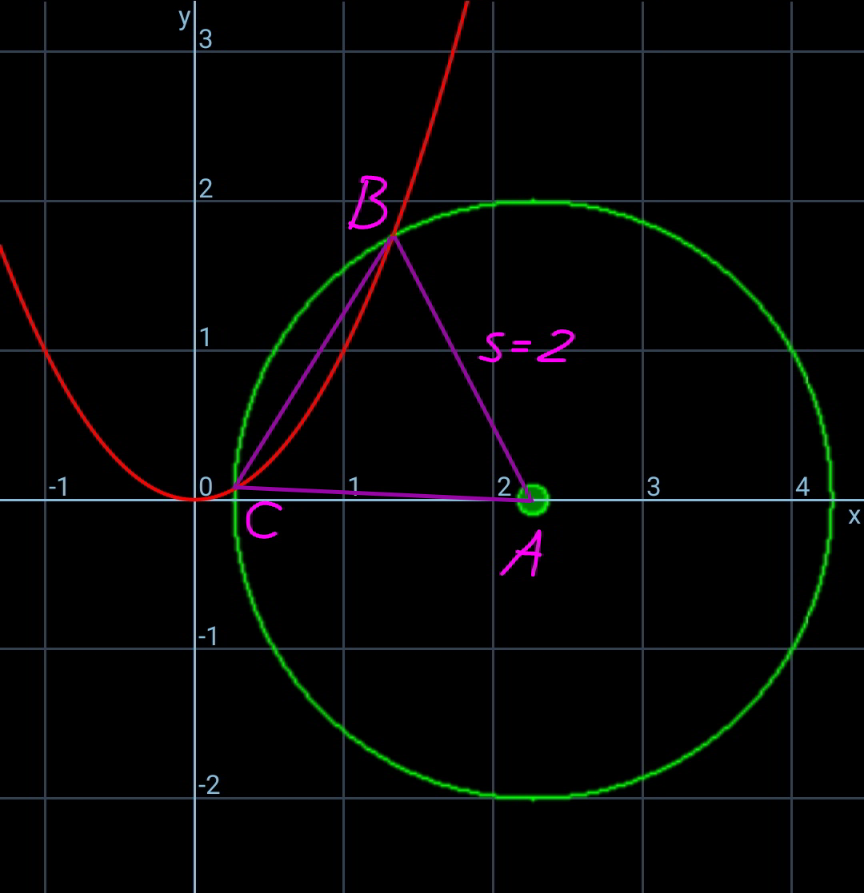
Commented by mr W last updated on 12/Dec/20
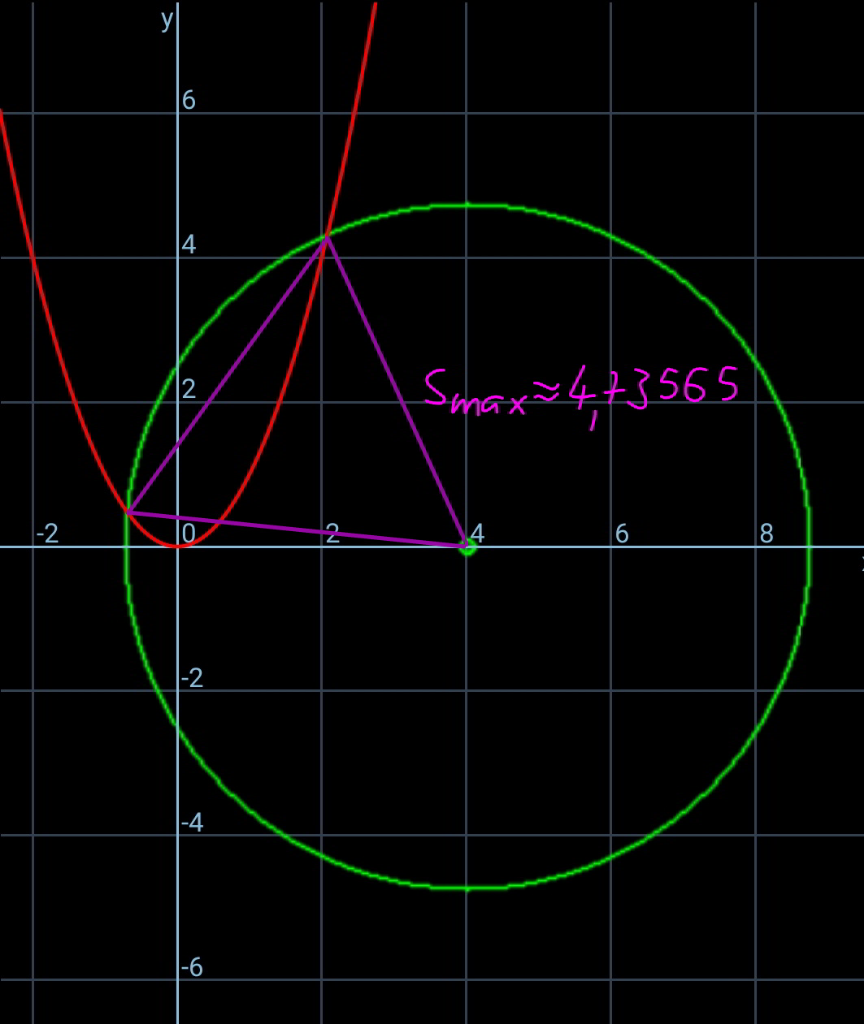
Commented by mr W last updated on 12/Dec/20
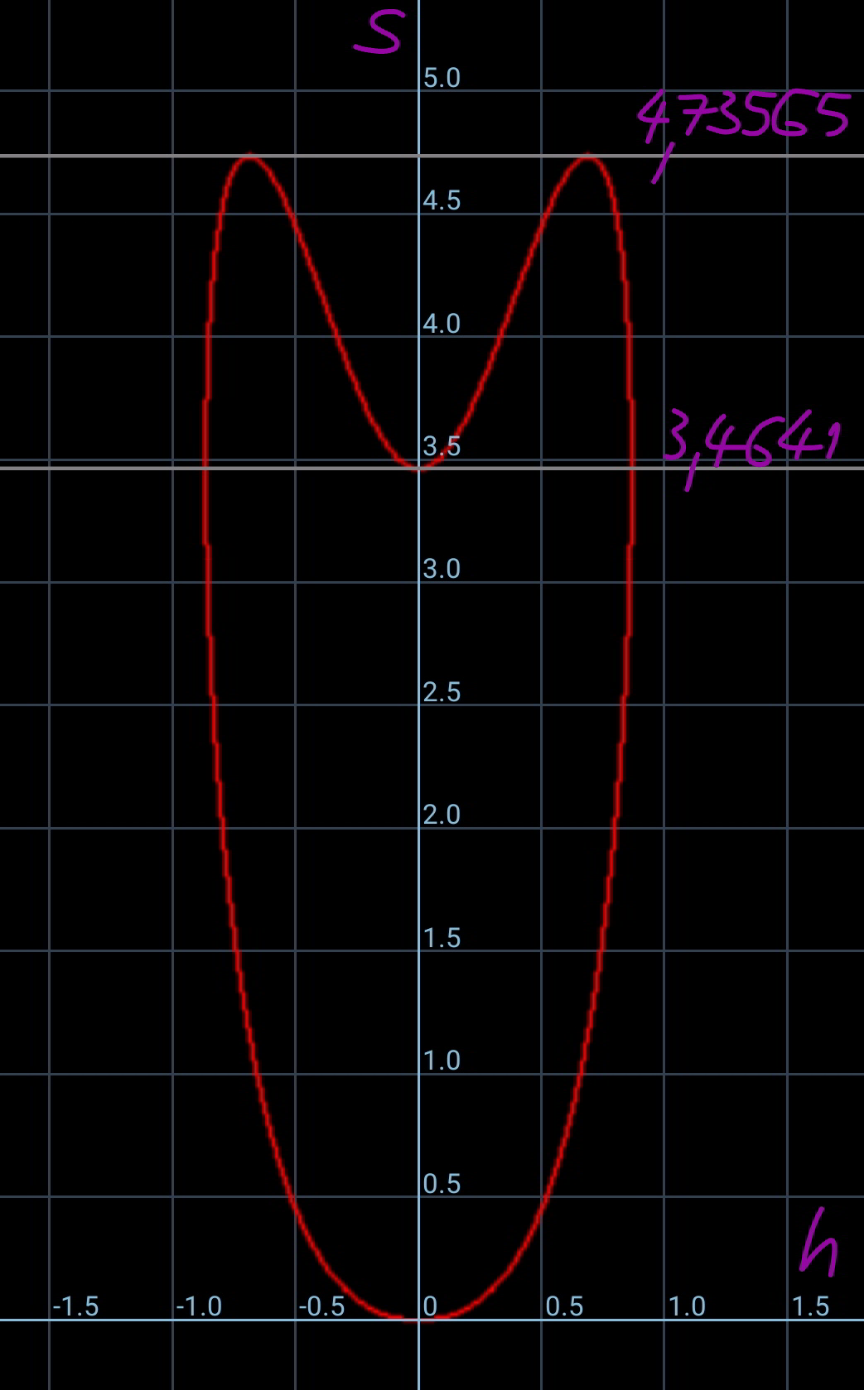
Commented by mr W last updated on 12/Dec/20
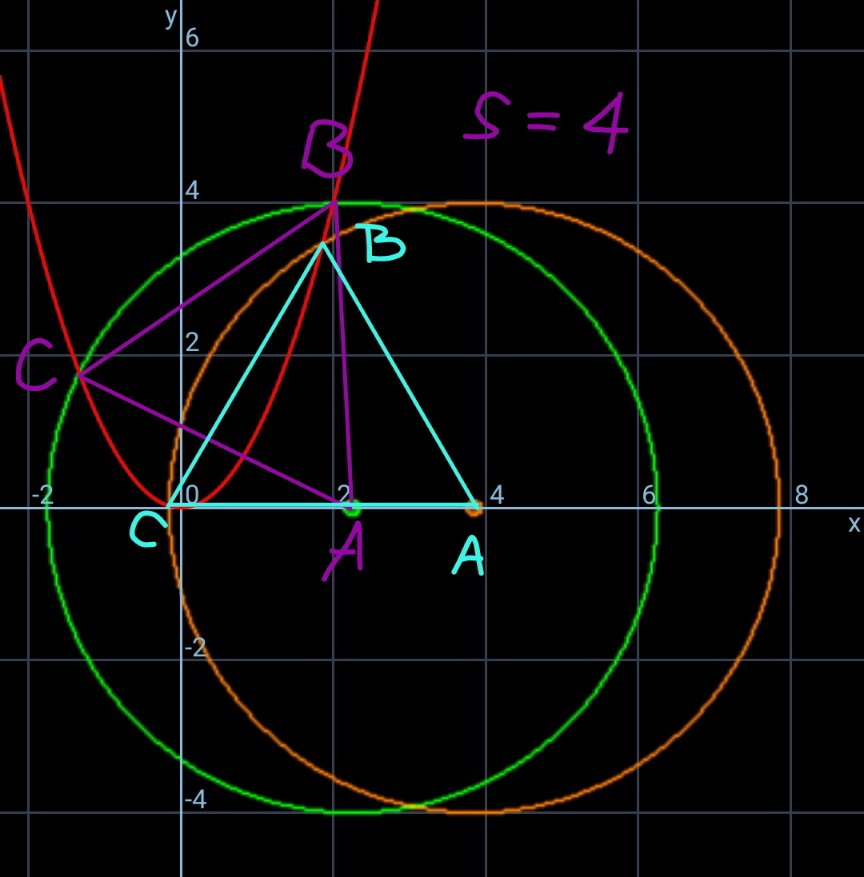
Commented by mr W last updated on 12/Dec/20
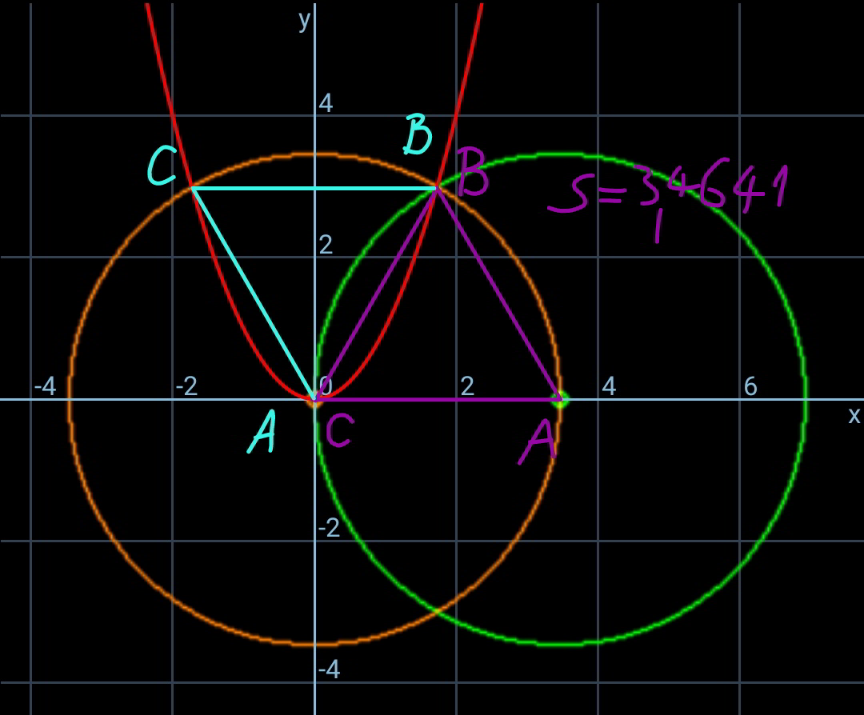
Answered by ajfour last updated on 12/Dec/20
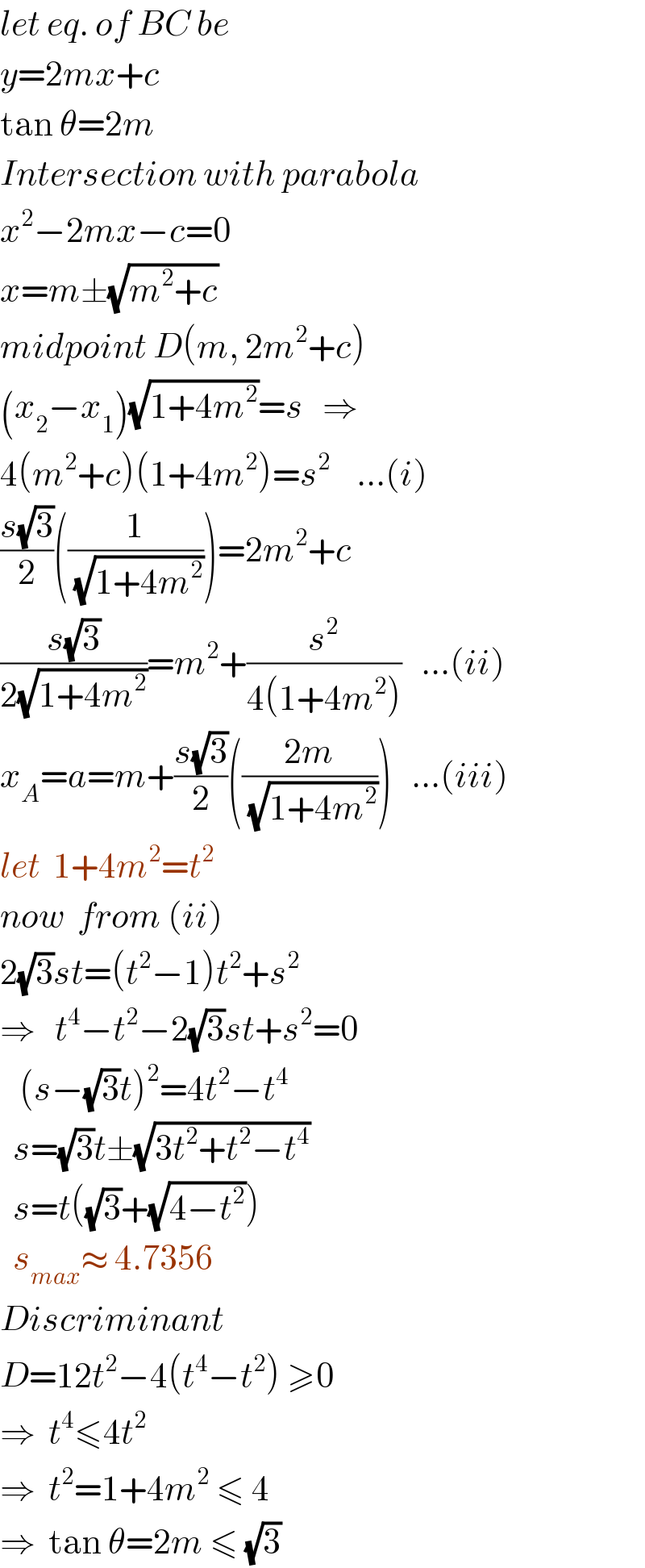
Commented by ajfour last updated on 12/Dec/20

Commented by ajfour last updated on 12/Dec/20
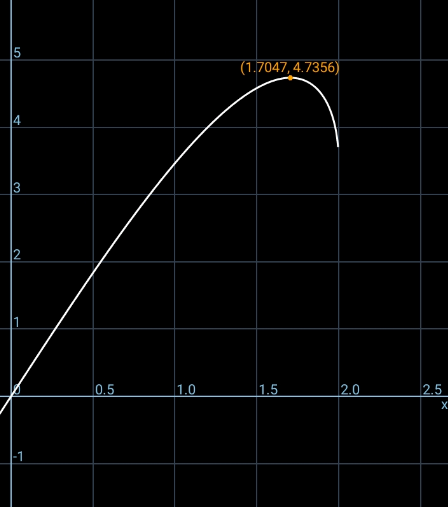
Commented by mr W last updated on 12/Dec/20
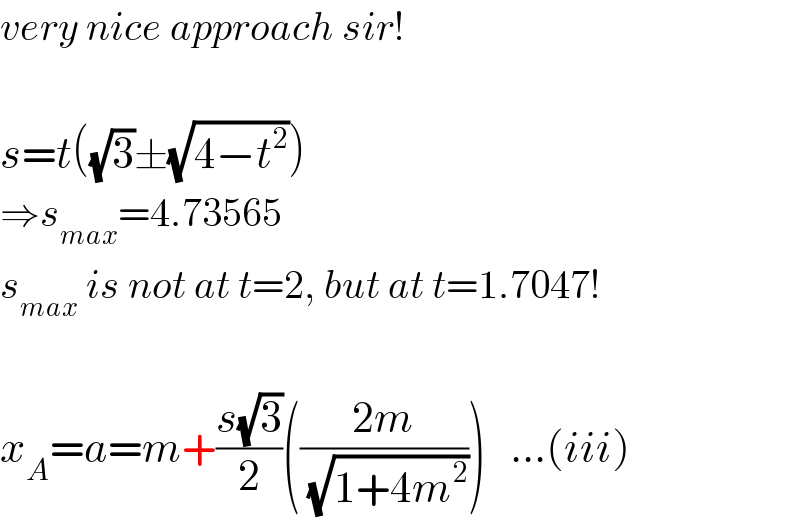
Commented by ajfour last updated on 12/Dec/20

Commented by mr W last updated on 12/Dec/20

Commented by ajfour last updated on 12/Dec/20

Commented by mr W last updated on 12/Dec/20

Commented by ajfour last updated on 12/Dec/20