Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 125685 by Hassen_Timol last updated on 12/Dec/20

$$$$$$\mathrm{Solve}\mathrm{this}\mathrm{differential}\mathrm{equation}$$$$$$$$q_{\left(t\right)}^{″}+\frac{1}{\mathrm{LC}}{q}_{\left(t\right)}=\frac{V}{L}$$$$$$$$\mathrm{with}(\mathrm{L},\mathrm{C},\mathrm{V})\in {\mathbb{R}}^3$$$$$$

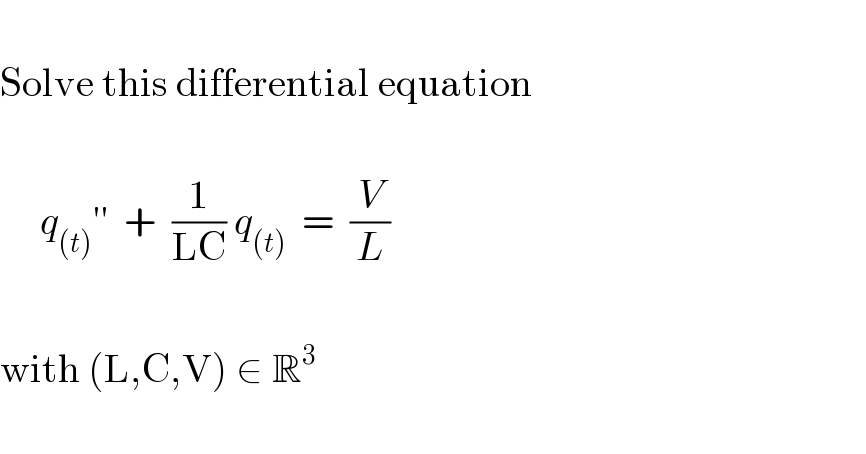
Answered by mr W last updated on 13/Dec/20

$$q\left(t\right)=A\cos \omega t+B\sin \omega t+VC$$$$with\omega =\sqrt{\frac{1}{LC}}$$

Commented by Hassen_Timol last updated on 13/Dec/20

$$\mathrm{Thank}\mathrm{you}\mathrm{a}\mathrm{lot}\mathrm{Sir}$$

Commented by Hassen_Timol last updated on 13/Dec/20

Isn't it ...+VC ? not VC² ? because V*L*C/L=VC

Commented by mr W last updated on 13/Dec/20

$$yes,VC.$$

Answered by mathmax by abdo last updated on 14/Dec/20

$$\mathrm{h}\to {\mathrm{r}}^2+\frac{1}{\mathrm{LC}}=0\Rightarrow \mathrm{r}=\stackrel{-}{+}\mathrm{i}\sqrt{\frac{1}{\mathrm{LC}}}\Rightarrow {\mathrm{q}}_{\mathrm{h}}\left(\mathrm{t}\right)={\mathrm{ae}}^{\mathrm{i}\sqrt{\frac{1}{\mathrm{LC}}}}+{\mathrm{be}}^{-\mathrm{i}\sqrt{\frac{1}{\mathrm{LC}}}}$$$$=\alpha \cos \left(\frac{\mathrm{t}}{\sqrt{\mathrm{LC}}}\right)+\beta \sin \left(\frac{\mathrm{t}}{\sqrt{\mathrm{LC}}}\right)=\alpha {\mathrm{u}}_1+\beta {\mathrm{u}}_2\mathrm{let}\mathrm{w}=\frac{1}{\sqrt{\mathrm{LC}}}$$$$\mathrm{W}({\mathrm{u}}_1,{\mathrm{u}}_2)=\left|\begin{array}{c}\cos \left(\mathrm{wt}\right)\sin \left(\mathrm{wt}\right)\\ -\mathrm{wsin}\left(\mathrm{wt}\right)\mathrm{wcos}\left(\mathrm{wt}\right)\end{array}\right|=\mathrm{w}\ne 0$$$${\mathrm{W}}_1=\left|\begin{array}{c}\mathrm{o}\sin \left(\mathrm{wt}\right)\\ \frac{\mathrm{V}}{\mathrm{L}}\mathrm{wcos}\left(\mathrm{wt}\right)\end{array}\right|=-\frac{\mathrm{V}}{\mathrm{L}}\sin \left(\mathrm{wt}\right)$$$${\mathrm{W}}_2=\left|\begin{array}{c}\cos \left(\mathrm{wt}\right)0\\ -\mathrm{wsin}\left(\mathrm{wt}\right)\frac{\mathrm{V}}{\mathrm{L}}\end{array}\right|=\frac{\mathrm{V}}{\mathrm{L}}\cos \left(\mathrm{wt}\right)$$$${\mathrm{v}}_1=\int \frac{{\mathrm{w}}_1}{\mathrm{w}}\mathrm{dt}=-\frac{\mathrm{V}}{\mathrm{L}}\int \frac{\sin \left(\mathrm{wt}\right)}{\mathrm{w}}\mathrm{dt}=-\frac{\mathrm{V}}{\mathrm{L}}\times \frac{1}{{\mathrm{w}}^2}\cos \left(\mathrm{wt}\right)$$$$=\frac{\mathrm{V}}{\mathrm{L}}\times \mathrm{LC}\cos \left(\mathrm{wt}\right)=\mathrm{VC}\cos \left(\mathrm{wt}\right)$$$${\mathrm{v}}_2=\int \frac{{\mathrm{w}}_2}{\mathrm{w}}\mathrm{dt}=\frac{\mathrm{V}}{\mathrm{L}}\int \frac{\cos \left(\mathrm{wt}\right)}{\mathrm{w}}\mathrm{dt}=\frac{\mathrm{V}}{\mathrm{L}}\times \frac{1}{{\mathrm{w}}^2}\sin \left(\mathrm{wt}\right)=\mathrm{VC}\sin \left(\mathrm{wt}\right)\Rightarrow$$$${\mathrm{q}}_{\mathrm{p}}={\mathrm{u}}_1{\mathrm{v}}_1+{\mathrm{u}}_2{\mathrm{v}}_2=\cos \left(\mathrm{wt}\right)\mathrm{VC}\cos \left(\mathrm{wt}\right)+\sin \left(\mathrm{wt}\right)\mathrm{VC}\sin \left(\mathrm{wt}\right)$$$$=\mathrm{VC}({\cos }^2\left(\mathrm{wt}\right)+{\sin }^2\left(\mathrm{wt}\right))=\mathrm{VC}\Rightarrow$$$$\mathrm{q}\left(\mathrm{t}\right)={\mathrm{q}}_{\mathrm{h}}\left(\mathrm{t}\right)+{\mathrm{q}}_{\mathrm{p}}\left(\mathrm{t}\right)=\alpha \cos \left(\mathrm{wt}\right)+\beta \sin \left(\mathrm{wt}\right)+\mathrm{VC}$$$$\mathrm{and}\mathrm{w}=\frac{1}{\sqrt{\mathrm{LC}}}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com