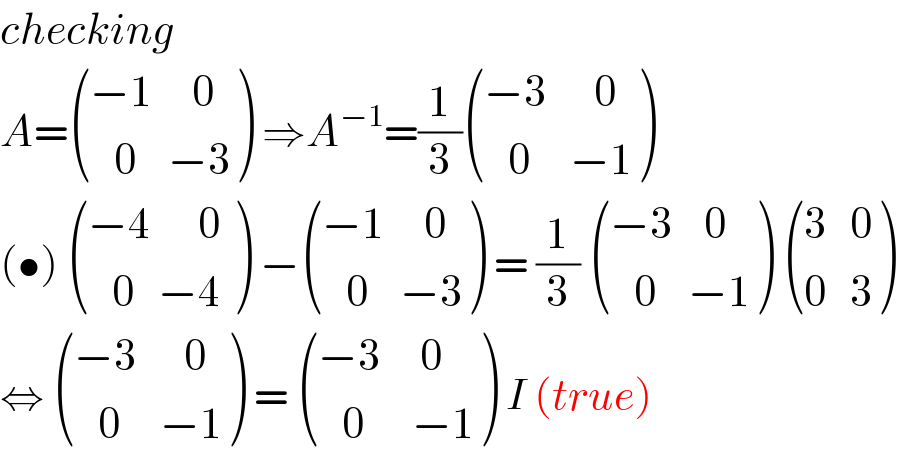Question and Answers Forum

All Questions      Topic List

Matrices and Determinants Questions

Previous in All Question      Next in All Question      

Previous in Matrices and Determinants      Next in Matrices and Determinants      

Question Number 125768 by Don08q last updated on 13/Dec/20

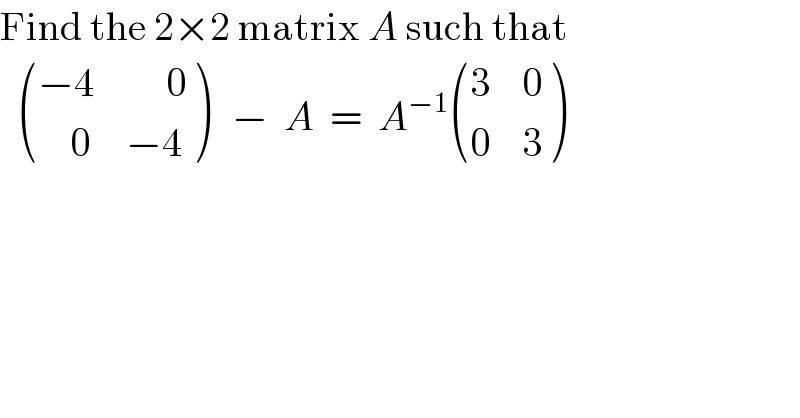
Find the 2×2 matrix A such that (((−4),( 0)),(( 0),(−4)) ) − A = A^(−1) ((3,0),(0,3) )

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{2}×\mathrm{2}\:\mathrm{matrix}\:{A}\:\mathrm{such}\:\mathrm{that} \\ $$$$\:\:\begin{pmatrix}{−\mathrm{4}}&{\:\:\:\:\:\mathrm{0}}\\{\:\:\:\:\mathrm{0}}&{−\mathrm{4}}\end{pmatrix}\:\:\:−\:\:{A}\:\:=\:\:{A}^{−\mathrm{1}} \begin{pmatrix}{\mathrm{3}}&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{3}}\end{pmatrix} \\ $$

Answered by 676597498 last updated on 13/Dec/20

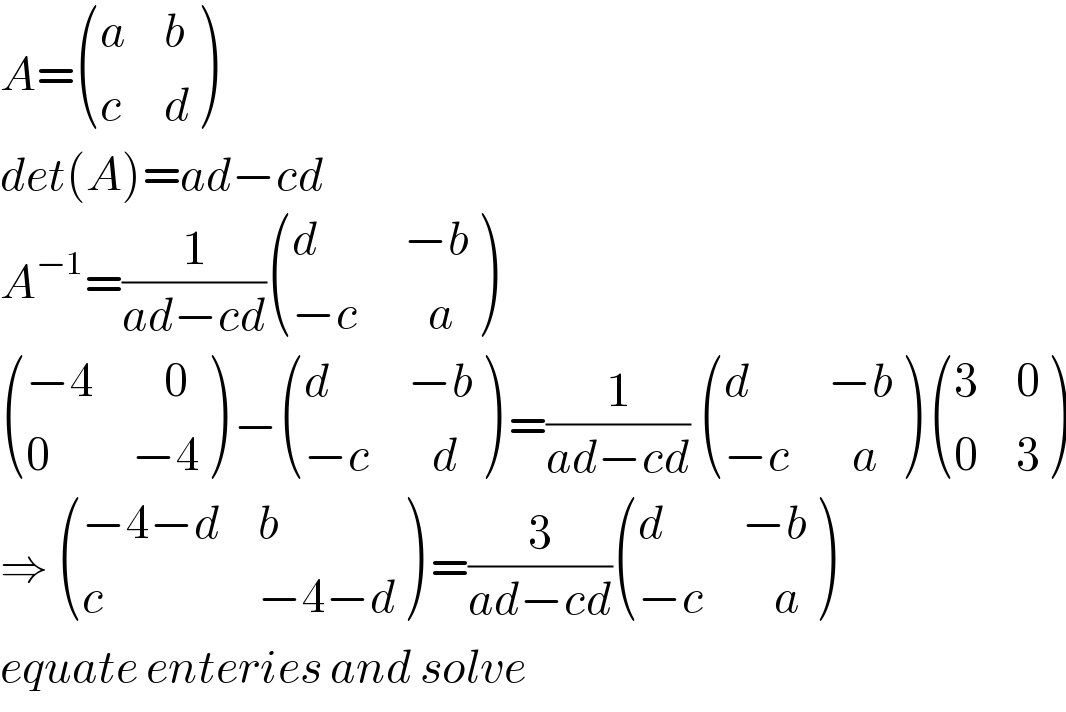
A= ((a,b),(c,d) ) det(A)=ad−cd A^(−1) =(1/(ad−cd)) ((d,(−b)),((−c ),( a)) ) (((−4),( 0)),(0,(−4)) ) − ((d,(−b)),((−c),( d)) ) =(1/(ad−cd)) ((d,(−b)),((−c),( a)) ) ((3,0),(0,3) ) ⇒ (((−4−d),b),(c,(−4−d)) ) =(3/(ad−cd)) ((d,(−b)),((−c),( a)) ) equate enteries and solve

$${A}=\begin{pmatrix}{{a}}&{{b}}\\{{c}}&{{d}}\end{pmatrix}\: \\ $$$${det}\left({A}\right)={ad}−{cd} \\ $$$${A}^{−\mathrm{1}} =\frac{\mathrm{1}}{{ad}−{cd}}\begin{pmatrix}{{d}}&{−{b}}\\{−{c}\:}&{\:\:\:{a}}\end{pmatrix} \\ $$$$\begin{pmatrix}{−\mathrm{4}}&{\:\:\:\:\mathrm{0}}\\{\mathrm{0}}&{−\mathrm{4}}\end{pmatrix}\:−\begin{pmatrix}{{d}}&{−{b}}\\{−{c}}&{\:\:\:{d}}\end{pmatrix}\:=\frac{\mathrm{1}}{{ad}−{cd}}\:\begin{pmatrix}{{d}}&{−{b}}\\{−{c}}&{\:\:\:{a}}\end{pmatrix}\:\begin{pmatrix}{\mathrm{3}}&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{3}}\end{pmatrix} \\ $$$$\Rightarrow\:\begin{pmatrix}{−\mathrm{4}−{d}}&{{b}}\\{{c}}&{−\mathrm{4}−{d}}\end{pmatrix}\:=\frac{\mathrm{3}}{{ad}−{cd}}\begin{pmatrix}{{d}}&{−{b}}\\{−{c}}&{\:\:\:\:{a}}\end{pmatrix} \\ $$$${equate}\:{enteries}\:{and}\:{solve} \\ $$

Answered by Olaf last updated on 13/Dec/20

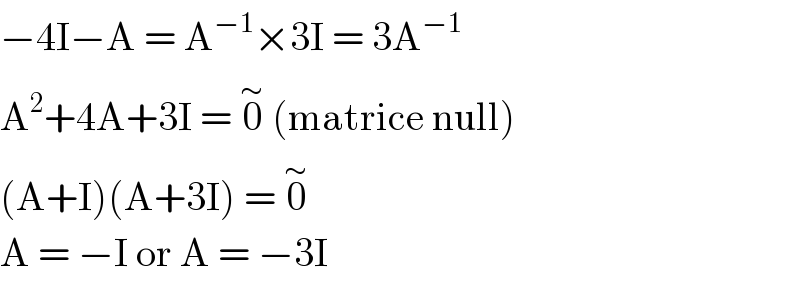
−4I−A = A^(−1) ×3I = 3A^(−1) A^2 +4A+3I = 0^∼ (matrice null) (A+I)(A+3I) = 0^∼ A = −I or A = −3I

$$−\mathrm{4I}−\mathrm{A}\:=\:\mathrm{A}^{−\mathrm{1}} ×\mathrm{3I}\:=\:\mathrm{3A}^{−\mathrm{1}} \\ $$$$\mathrm{A}^{\mathrm{2}} +\mathrm{4A}+\mathrm{3I}\:=\:\overset{\sim} {\mathrm{0}}\:\left(\mathrm{matrice}\:\mathrm{null}\right) \\ $$$$\left(\mathrm{A}+\mathrm{I}\right)\left(\mathrm{A}+\mathrm{3I}\right)\:=\:\overset{\sim} {\mathrm{0}} \\ $$$$\mathrm{A}\:=\:−\mathrm{I}\:\mathrm{or}\:\mathrm{A}\:=\:−\mathrm{3I} \\ $$

Commented by mindispower last updated on 13/Dec/20

AM=0⇏A=0 or M=0 (((0 0)),((1 0)) ). (((0 0)),((1 0 )) )=0

$${AM}=\mathrm{0}\nRightarrow{A}=\mathrm{0}\:{or}\:{M}=\mathrm{0} \\ $$$$\begin{pmatrix}{\mathrm{0}\:\:\:\:\mathrm{0}}\\{\mathrm{1}\:\:\:\:\mathrm{0}}\end{pmatrix}.\begin{pmatrix}{\mathrm{0}\:\:\:\:\mathrm{0}}\\{\mathrm{1}\:\:\:\:\mathrm{0}\:\:\:\:\:}\end{pmatrix}=\mathrm{0} \\ $$

Commented by Olaf last updated on 14/Dec/20

Sure sir but in your example the determinant of A and M are 0. It′s not the case in the exercise and we verify that the two solutions found are really solutions... of course.

$$\mathrm{Sure}\:\mathrm{sir}\:\mathrm{but}\:\mathrm{in}\:\mathrm{your}\:\mathrm{example} \\ $$$$\mathrm{the}\:\mathrm{determinant}\:\mathrm{of}\:\mathrm{A}\:\mathrm{and}\:\mathrm{M}\:\mathrm{are}\:\mathrm{0}. \\ $$$$\mathrm{It}'\mathrm{s}\:\mathrm{not}\:\mathrm{the}\:\mathrm{case}\:\mathrm{in}\:\mathrm{the}\:\mathrm{exercise}\:\mathrm{and}\:\mathrm{we} \\ $$$$\mathrm{verify}\:\mathrm{that}\:\mathrm{the}\:\mathrm{two}\:\mathrm{solutions}\:\mathrm{found} \\ $$$$\mathrm{are}\:\mathrm{really}\:\mathrm{solutions}...\:\mathrm{of}\:\mathrm{course}. \\ $$

Answered by liberty last updated on 13/Dec/20

(((a b)),((c d)) ) [ (((−4 0)),(( 0 −4)) )− (((a b)),((c d)) ) ] = (((3 0)),((0 3)) ) (((a b)),((c d)) ) (((−4−a − b)),(( −c −4−d)) ) = (((3 0)),((0 3)) ) (((−a^2 −4a−bc −ab−4b−bd)),((−ac−4c−cd −bc−4d−d^2 )) ) = (((3 0)),((0 3)) ) (•) −ab−4b−bd=0 ; b(a+4+d)=0 → { ((b=0)),((a+d=−4)) :} (••)−ac−4c−cd=0 ; c(a+d+4)=0→ { ((c=0)),((a+d=−4)) :} for b=0 ⇒−a^2 −4a=3 ; a^2 +4a+3=0 (a+1)(a+3)=0→ { ((a=−1 ∧d=−3)),((a=−3 ∧d=−1)) :} A= (((−1 0)),(( 0 −3)) ) or A= (((−3 0)),(( 0 −1)) )

$$\begin{pmatrix}{{a}\:\:\:\:{b}}\\{{c}\:\:\:\:{d}}\end{pmatrix}\:\left[\:\begin{pmatrix}{−\mathrm{4}\:\:\:\:\:\:\mathrm{0}}\\{\:\:\:\mathrm{0}\:\:\:\:\:−\mathrm{4}}\end{pmatrix}−\begin{pmatrix}{{a}\:\:\:\:\:{b}}\\{{c}\:\:\:\:\:\:{d}}\end{pmatrix}\:\right]\:=\:\begin{pmatrix}{\mathrm{3}\:\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\:\mathrm{3}}\end{pmatrix} \\ $$$$\begin{pmatrix}{{a}\:\:\:\:{b}}\\{{c}\:\:\:\:{d}}\end{pmatrix}\:\begin{pmatrix}{−\mathrm{4}−{a}\:\:\:\:\:\:\:\:−\:{b}}\\{\:\:\:\:\:\:−{c}\:\:\:\:\:\:−\mathrm{4}−{d}}\end{pmatrix}\:=\:\begin{pmatrix}{\mathrm{3}\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\:\:\mathrm{3}}\end{pmatrix} \\ $$$$\begin{pmatrix}{−{a}^{\mathrm{2}} −\mathrm{4}{a}−{bc}\:\:\:\:\:\:\:\:−{ab}−\mathrm{4}{b}−{bd}}\\{−{ac}−\mathrm{4}{c}−{cd}\:\:\:\:\:\:\:\:−{bc}−\mathrm{4}{d}−{d}^{\mathrm{2}} }\end{pmatrix}\:=\:\begin{pmatrix}{\mathrm{3}\:\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\:\mathrm{3}}\end{pmatrix} \\ $$$$\left(\bullet\right)\:−{ab}−\mathrm{4}{b}−{bd}=\mathrm{0}\:;\:{b}\left({a}+\mathrm{4}+{d}\right)=\mathrm{0}\:\rightarrow\begin{cases}{{b}=\mathrm{0}}\\{{a}+{d}=−\mathrm{4}}\end{cases} \\ $$$$\left(\bullet\bullet\right)−{ac}−\mathrm{4}{c}−{cd}=\mathrm{0}\:;\:{c}\left({a}+{d}+\mathrm{4}\right)=\mathrm{0}\rightarrow\begin{cases}{{c}=\mathrm{0}}\\{{a}+{d}=−\mathrm{4}}\end{cases} \\ $$$${for}\:{b}=\mathrm{0}\:\Rightarrow−{a}^{\mathrm{2}} −\mathrm{4}{a}=\mathrm{3}\:;\:{a}^{\mathrm{2}} +\mathrm{4}{a}+\mathrm{3}=\mathrm{0} \\ $$$$\:\left({a}+\mathrm{1}\right)\left({a}+\mathrm{3}\right)=\mathrm{0}\rightarrow\begin{cases}{{a}=−\mathrm{1}\:\wedge{d}=−\mathrm{3}}\\{{a}=−\mathrm{3}\:\wedge{d}=−\mathrm{1}}\end{cases} \\ $$$${A}=\begin{pmatrix}{−\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{0}}\\{\:\:\:\:\mathrm{0}\:\:\:\:\:\:−\mathrm{3}}\end{pmatrix}\:{or}\:{A}=\begin{pmatrix}{−\mathrm{3}\:\:\:\:\:\:\mathrm{0}}\\{\:\:\:\mathrm{0}\:\:\:\:\:−\mathrm{1}}\end{pmatrix} \\ $$

Commented by liberty last updated on 13/Dec/20

checking A= (((−1 0)),(( 0 −3)) ) ⇒A^(−1) =(1/3) (((−3 0)),(( 0 −1)) ) (•) (((−4 0 )),(( 0 −4)) ) − (((−1 0)),(( 0 −3)) ) = (1/3) (((−3 0)),(( 0 −1)) ) (((3 0)),((0 3)) ) ⇔ (((−3 0)),(( 0 −1)) ) = (((−3 0)),(( 0 −1)) ) I (true)

$${checking} \\ $$$${A}=\begin{pmatrix}{−\mathrm{1}\:\:\:\:\:\mathrm{0}}\\{\:\:\:\mathrm{0}\:\:\:\:−\mathrm{3}}\end{pmatrix}\:\Rightarrow{A}^{−\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{3}}\begin{pmatrix}{−\mathrm{3}\:\:\:\:\:\:\mathrm{0}}\\{\:\:\:\mathrm{0}\:\:\:\:\:−\mathrm{1}}\end{pmatrix} \\ $$$$\left(\bullet\right)\:\begin{pmatrix}{−\mathrm{4}\:\:\:\:\:\:\mathrm{0}\:}\\{\:\:\:\mathrm{0}\:\:\:−\mathrm{4}}\end{pmatrix}\:−\begin{pmatrix}{−\mathrm{1}\:\:\:\:\:\mathrm{0}}\\{\:\:\:\mathrm{0}\:\:\:\:−\mathrm{3}}\end{pmatrix}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:\begin{pmatrix}{−\mathrm{3}\:\:\:\:\mathrm{0}}\\{\:\:\:\mathrm{0}\:\:\:\:−\mathrm{1}}\end{pmatrix}\:\begin{pmatrix}{\mathrm{3}\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\mathrm{3}}\end{pmatrix} \\ $$$$\Leftrightarrow\:\begin{pmatrix}{−\mathrm{3}\:\:\:\:\:\:\mathrm{0}}\\{\:\:\:\mathrm{0}\:\:\:\:\:−\mathrm{1}}\end{pmatrix}\:=\:\begin{pmatrix}{−\mathrm{3}\:\:\:\:\:\mathrm{0}}\\{\:\:\:\mathrm{0}\:\:\:\:\:\:−\mathrm{1}}\end{pmatrix}\:{I}\:\left({true}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com