Question Number 125782 by ajfour last updated on 13/Dec/20
Commented by ajfour last updated on 13/Dec/20
$${Find}\:{radius}\:{of}\:{the}\:{smaller}\:{circle}. \\ $$
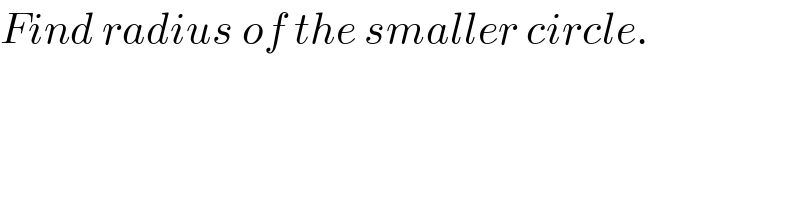
Commented by MJS_new last updated on 14/Dec/20
$$\mathrm{sorry}\:\mathrm{I}\:\mathrm{have}\:\mathrm{no}\:\mathrm{time}... \\ $$$$\mathrm{can}\:\mathrm{we}\:\mathrm{find}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{all}\:\mathrm{circles} \\ $$$$\left({x}−{m}\right)^{\mathrm{2}} +\left({y}−{n}\right)^{\mathrm{2}} ={n}^{\mathrm{2}} \:\mathrm{with}\:\mathrm{0}\leqslant{m}\leqslant{a} \\ $$$$\mathrm{touching}\:\mathrm{the}\:\mathrm{upper}\:\mathrm{half}\:\mathrm{ellipse} \\ $$$${y}=\frac{\mathrm{1}}{{a}}\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }\:\mathrm{with}\:\mathrm{1}<{a} \\ $$$$\mathrm{as}\:\mathrm{a}\:\mathrm{first}\:\mathrm{step}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{this}\:\mathrm{problem}? \\ $$
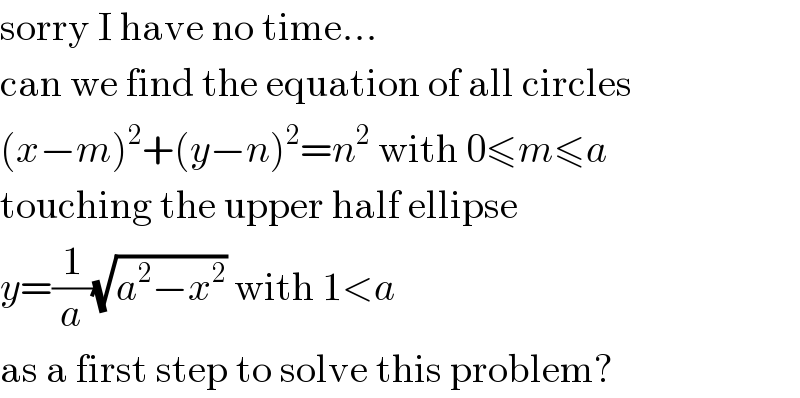
Answered by mr W last updated on 14/Dec/20
![let μ=(b/a), λ=(r/a) say P(a cos θ, b sin θ) tan ϕ=−((b cos θ)/(−a sin θ))=(μ/(tan θ)) a cos θ=(√(((b/2)+r)^2 −((b/2)−r)^2 ))+r sin ϕ ⇒a cos θ=(√(2br))+((μr)/( (√(μ^2 +tan^2 θ)))) ...(i) b sin θ=r+r cos ϕ ⇒b sin θ=r[1+((tan θ)/( (√(μ^2 +tan^2 θ))))] ...(ii) (ii)÷(i): μ tan θ=((r[1+((tan θ)/( (√(μ^2 +tan^2 θ))))])/( (√(2br))+((rμ)/( (√(μ^2 +tan^2 θ)))))) let t=tan^2 θ μt=(((√λ)[1+(t/( (√(μ^2 +t^2 ))))])/( (√(2μ))+(((√λ)μ)/( (√(μ^2 +t^2 )))))) (√λ)[1+(t/( (√(μ^2 +t^2 ))))]=(((√λ)μ^2 t)/( (√(μ^2 +t^2 ))))+μt(√(2μ)) ⇒λ=((2μ^3 t^2 )/([1+(((1−μ^2 )t)/( (√(μ^2 +t^2 ))))]^2 )) ...(I) from (ii): ((μt)/( (√(1+t^2 ))))=λ[1+(t/( (√(μ^2 +t^2 ))))] ⇒λ=((μt)/( (√(1+t^2 ))[1+(t/( (√(μ^2 +t^2 ))))])) ...(II) ⇒[1+(((1−μ^2 )t)/( (√(μ^2 +t^2 ))))]^2 =2μ^2 t(√(1+t^2 ))[1+(t/( (√(μ^2 +t^2 ))))] ...(III) we can get t from (III) and then λ from (I) or (II).](Q125825.png)
$${let}\:\mu=\frac{{b}}{{a}},\:\lambda=\frac{{r}}{{a}} \\ $$$${say}\:{P}\left({a}\:\mathrm{cos}\:\theta,\:{b}\:\mathrm{sin}\:\theta\right) \\ $$$$\mathrm{tan}\:\varphi=−\frac{{b}\:\mathrm{cos}\:\theta}{−{a}\:\mathrm{sin}\:\theta}=\frac{\mu}{\mathrm{tan}\:\theta} \\ $$$${a}\:\mathrm{cos}\:\theta=\sqrt{\left(\frac{{b}}{\mathrm{2}}+{r}\right)^{\mathrm{2}} −\left(\frac{{b}}{\mathrm{2}}−{r}\right)^{\mathrm{2}} }+{r}\:\mathrm{sin}\:\varphi \\ $$$$\Rightarrow{a}\:\mathrm{cos}\:\theta=\sqrt{\mathrm{2}{br}}+\frac{\mu{r}}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\theta}}\:\:\:...\left({i}\right) \\ $$$${b}\:\mathrm{sin}\:\:\theta={r}+{r}\:\mathrm{cos}\:\varphi \\ $$$$\Rightarrow{b}\:\mathrm{sin}\:\:\theta={r}\left[\mathrm{1}+\frac{\mathrm{tan}\:\theta}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\theta}}\right]\:\:\:...\left({ii}\right) \\ $$$$\left({ii}\right)\boldsymbol{\div}\left({i}\right): \\ $$$$\mu\:\mathrm{tan}\:\theta=\frac{{r}\left[\mathrm{1}+\frac{\mathrm{tan}\:\theta}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\theta}}\right]}{\:\sqrt{\mathrm{2}{br}}+\frac{{r}\mu}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\theta}}} \\ $$$${let}\:{t}=\mathrm{tan}^{\mathrm{2}} \:\theta \\ $$$$\mu{t}=\frac{\sqrt{\lambda}\left[\mathrm{1}+\frac{\mathrm{t}}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{t}^{\mathrm{2}} }}\right]}{\:\sqrt{\mathrm{2}\mu}+\frac{\sqrt{\lambda}\mu}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{t}^{\mathrm{2}} }}} \\ $$$$\sqrt{\lambda}\left[\mathrm{1}+\frac{\mathrm{t}}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{t}^{\mathrm{2}} }}\right]=\frac{\sqrt{\lambda}\mu^{\mathrm{2}} {t}}{\:\sqrt{\mu^{\mathrm{2}} +{t}^{\mathrm{2}} }}+\mu{t}\sqrt{\mathrm{2}\mu} \\ $$$$\Rightarrow\lambda=\frac{\mathrm{2}\mu^{\mathrm{3}} {t}^{\mathrm{2}} }{\left[\mathrm{1}+\frac{\left(\mathrm{1}−\mu^{\mathrm{2}} \right){t}}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{t}^{\mathrm{2}} }}\right]^{\mathrm{2}} }\:\:\:...\left({I}\right) \\ $$$${from}\:\left({ii}\right): \\ $$$$\frac{\mu{t}}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}=\lambda\left[\mathrm{1}+\frac{\mathrm{t}}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{t}^{\mathrm{2}} }}\right] \\ $$$$\Rightarrow\lambda=\frac{\mu{t}}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\left[\mathrm{1}+\frac{\mathrm{t}}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{t}^{\mathrm{2}} }}\right]}\:\:\:...\left({II}\right) \\ $$$$\Rightarrow\left[\mathrm{1}+\frac{\left(\mathrm{1}−\mu^{\mathrm{2}} \right){t}}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{t}^{\mathrm{2}} }}\right]^{\mathrm{2}} =\mathrm{2}\mu^{\mathrm{2}} {t}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\left[\mathrm{1}+\frac{\mathrm{t}}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{t}^{\mathrm{2}} }}\right]\:\:\:...\left({III}\right) \\ $$$${we}\:{can}\:{get}\:{t}\:{from}\:\left({III}\right)\:{and}\:{then}\:\lambda \\ $$$${from}\:\left({I}\right)\:{or}\:\left({II}\right). \\ $$
Commented by mr W last updated on 14/Dec/20
Commented by mr W last updated on 14/Dec/20
Commented by mr W last updated on 14/Dec/20
Commented by ajfour last updated on 14/Dec/20
$${Perfectly}\:{well}\:{managed},\:{Sir}! \\ $$$${Very}\:{pragmatic}\:{and}\:{wise}\:{sol}^{{n}} . \\ $$