
Question and Answers Forum
Previous in Differential Equation Next in Differential Equation
Question Number 125958 by bramlexs22 last updated on 15/Dec/20
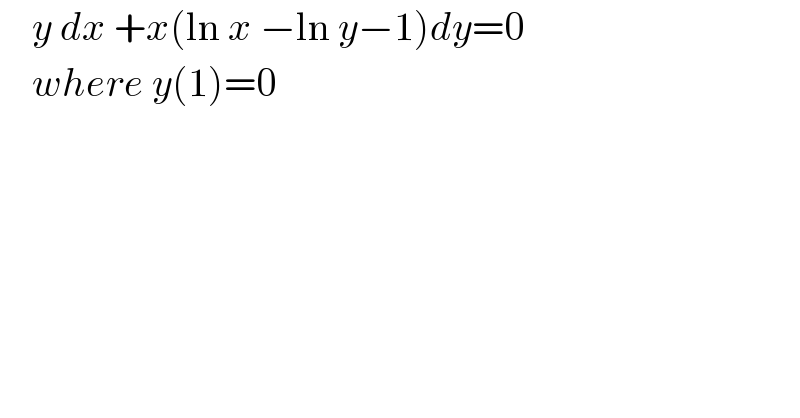
Answered by Olaf last updated on 16/Dec/20
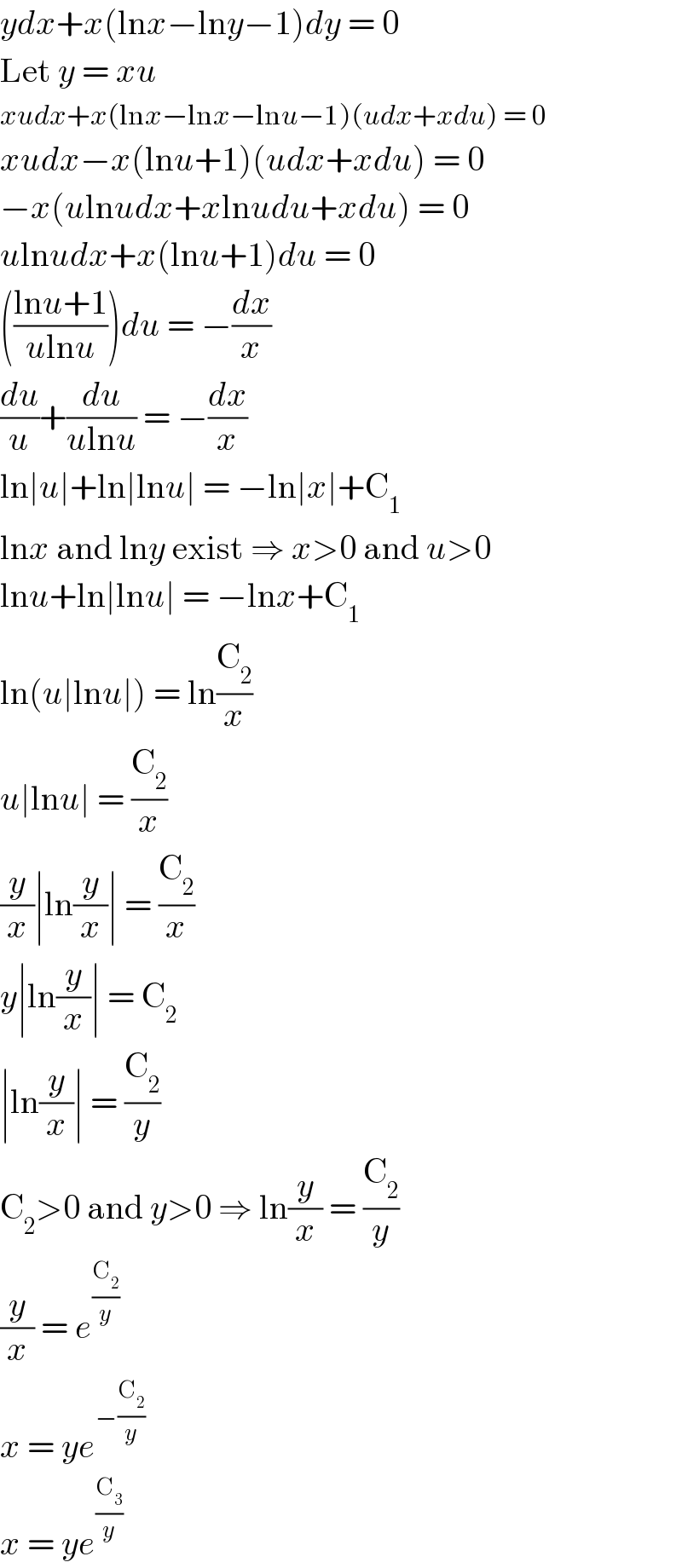
Answered by liberty last updated on 17/Dec/20
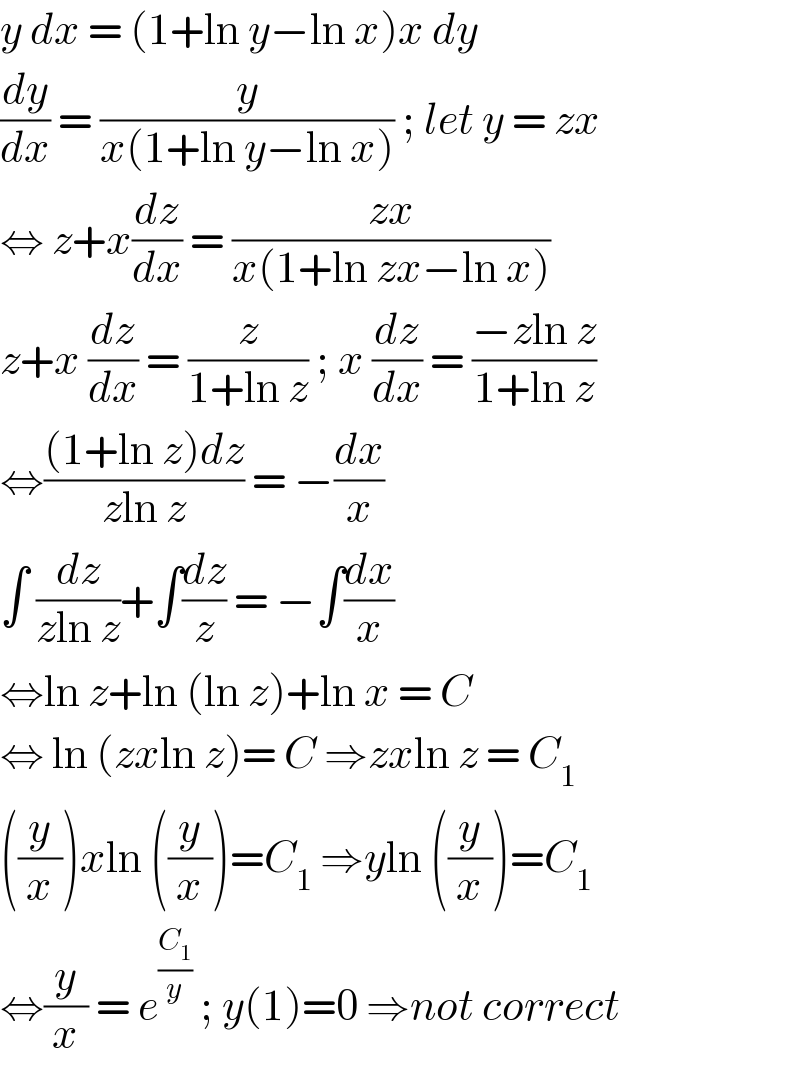
| ||
Question and Answers Forum | ||
Previous in Differential Equation Next in Differential Equation | ||
Question Number 125958 by bramlexs22 last updated on 15/Dec/20 | ||
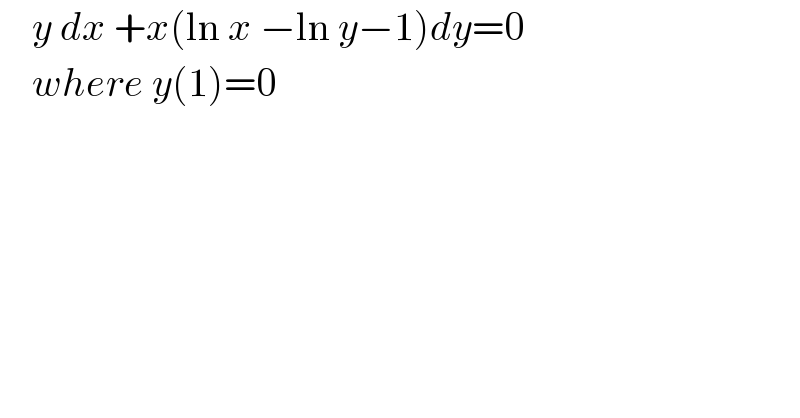 | ||
Answered by Olaf last updated on 16/Dec/20 | ||
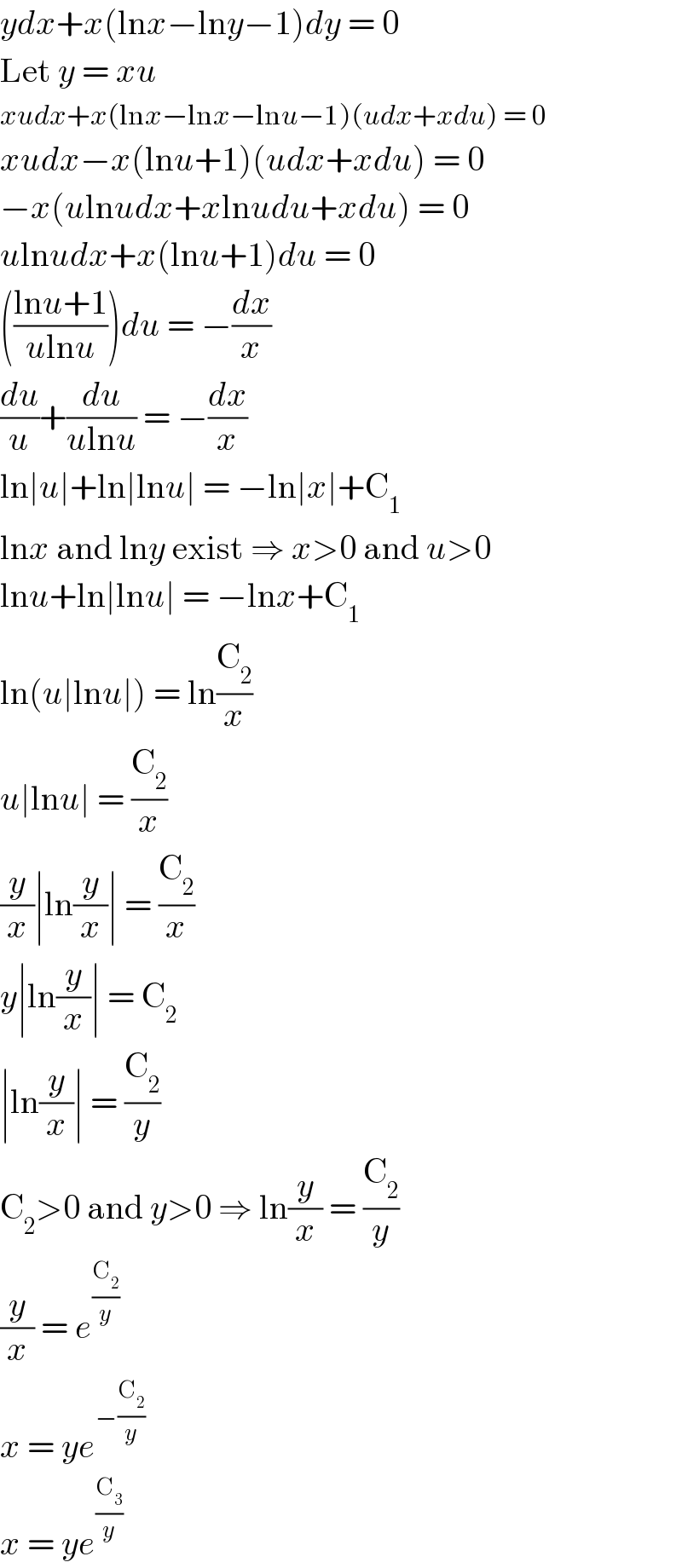 | ||
| ||
Answered by liberty last updated on 17/Dec/20 | ||
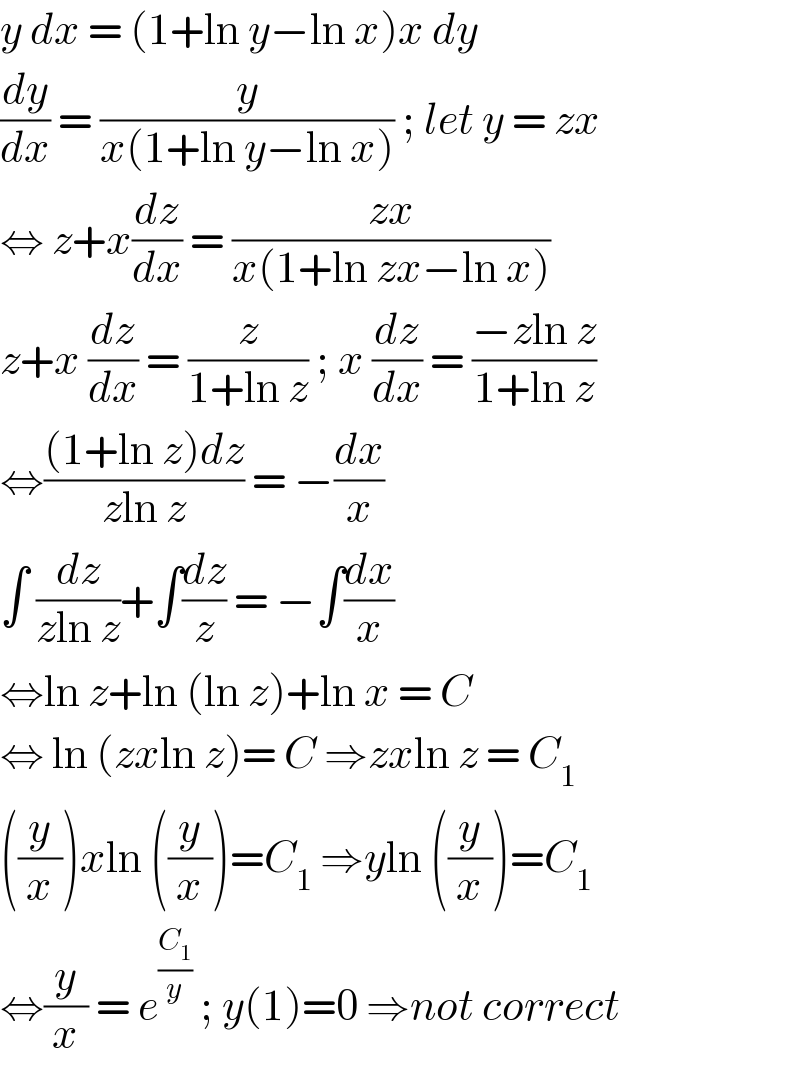 | ||
| ||