Math Question and Answers


Question and Answers Forum

All Questions Topic List
Differentiation Questions
Previous in All Question Next in All Question
Previous in Differentiation Next in Differentiation
Question Number 126003 by mnjuly1970 last updated on 16/Dec/20

$. . . n i c e i n t e g r a l . . .$ $p r o v e t h a t ::$ $ϕ = \int_{0}^{\frac{π}{2}} t a n (x) l n (s i n (x)) l n (c o s (x)) d x = \frac{ζ (3}{8}$ $G o o d l u c k$
	Answered by Olaf last updated on 16/Dec/20
	$φ = ∫_0 ^(π/2) tanxln(cosx)ln(sinx)dx φ = −∫_0 ^(π/2) [−tanxln(cosx)]ln(sinx)dx φ = −[(1/2)ln^2 (cosx)ln(sinx)]_0 ^(π/2) +∫_0 ^(π/2) [(1/2)ln^2 (cosx)]cotxdx φ = (1/2)∫_0 ^(π/2) cotx.ln^2 (cosx)dx Let u = cosx du = −sinxdx = −(√(1−u^2 ))dx φ = (1/2)∫_1 ^0 (u/( (√(1−u^2 ))))ln^2 u(−(du/( (√(1−u^2 ))))) φ = (1/2)∫_0 ^1 (u/( 1−u^2 ))ln^2 udu φ = (1/2)∫_0 ^1 u.ln^2 uΣ_(n=0) ^∞ u^(2n) du φ = (1/2)Σ_(n=0) ^∞ ∫_0 ^1 u^(2n+1) ln^2 udu φ = (1/2)Σ_(n=0) ^∞ {[(u^(2n+2) /(2n+2))ln^2 u]_0 ^1 −∫_0 ^1 (u^(2n+2) /(2n+2))(2((lnu)/u))du} φ = (1/2)Σ_(n=0) ^∞ {−∫_0 ^1 (u^(2n+2) /(2n+2))(2((lnu)/u))du} φ = −Σ_(n=0) ^∞ ∫_0 ^1 (u^(2n+1) /(2n+2))lnudu φ = −Σ_(n=0) ^∞ {[(u^(2n+2) /((2n+2)^2 ))lnu]_0 ^1 −∫_0 ^1 (u^(2n+2) /((2n+2)^2 )).(du/u)} φ = Σ_(n=0) ^∞ ∫_0 ^1 (u^(2n+2) /((2n+2)^2 )).(du/u) φ = Σ_(n=0) ^∞ ∫_0 ^1 (u^(2n+1) /((2n+2)^2 )).du φ = Σ_(n=0) ^∞ [(u^(2n+2) /((2n+2)^3 ))]_0 ^1 φ = Σ_(n=0) ^∞ (1/((2n+2)^3 )) φ = (1/8)Σ_(n=0) ^∞ (1/((n+1)^3 )) φ = (1/8)Σ_(n=1) ^∞ (1/n^3 ) φ = ((ζ(3))/8)$
	$ϕ = \int_{0}^{\frac{π}{2}} \tan x \ln (\cos x) \ln (\sin x) d x$ $ϕ = - \int_{0}^{\frac{π}{2}} [- \tan x \ln (\cos x)] \ln (\sin x) d x$ $ϕ = - {[\frac{1}{2} \ln^{2} (\cos x) \ln (\sin x)]}_{0}^{\frac{π}{2}}$ $+ \int_{0}^{\frac{π}{2}} [\frac{1}{2} \ln^{2} (\cos x)] \cot x d x$ $ϕ = \frac{1}{2} \int_{0}^{\frac{π}{2}} \cot x . \ln^{2} (\cos x) d x$ $Let u = \cos x$ $d u = - \sin x d x = - \sqrt{1 - u^{2}} d x$ $ϕ = \frac{1}{2} \int_{1}^{0} \frac{u}{\sqrt{1 - u^{2}}} \ln^{2} u (- \frac{d u}{\sqrt{1 - u^{2}}})$ $ϕ = \frac{1}{2} \int_{0}^{1} \frac{u}{1 - u^{2}} \ln^{2} u d u$ $ϕ = \frac{1}{2} \int_{0}^{1} u . \ln^{2} u \underset{n = 0}{\sum^{\infty}} u^{2 n} d u$ $ϕ = \frac{1}{2} \underset{n = 0}{\sum^{\infty}} \int_{0}^{1} u^{2 n + 1} \ln^{2} u d u$ $ϕ = \frac{1}{2} \underset{n = 0}{\sum^{\infty}} {{[\frac{u^{2 n + 2}}{2 n + 2} \ln^{2} u]}_{0}^{1} - \int_{0}^{1} \frac{u^{2 n + 2}}{2 n + 2} (2 \frac{\ln u}{u}) d u}$ $ϕ = \frac{1}{2} \underset{n = 0}{\sum^{\infty}} {- \int_{0}^{1} \frac{u^{2 n + 2}}{2 n + 2} (2 \frac{\ln u}{u}) d u}$ $ϕ = - \underset{n = 0}{\sum^{\infty}} \int_{0}^{1} \frac{u^{2 n + 1}}{2 n + 2} \ln u d u$ $ϕ = - \underset{n = 0}{\sum^{\infty}} {{[\frac{u^{2 n + 2}}{{(2 n + 2)}^{2}} \ln u]}_{0}^{1} - \int_{0}^{1} \frac{u^{2 n + 2}}{{(2 n + 2)}^{2}} . \frac{d u}{u}}$ $ϕ = \underset{n = 0}{\sum^{\infty}} \int_{0}^{1} \frac{u^{2 n + 2}}{{(2 n + 2)}^{2}} . \frac{d u}{u}$ $ϕ = \underset{n = 0}{\sum^{\infty}} \int_{0}^{1} \frac{u^{2 n + 1}}{{(2 n + 2)}^{2}} . d u$ $ϕ = \underset{n = 0}{\sum^{\infty}} {[\frac{u^{2 n + 2}}{{(2 n + 2)}^{3}}]}_{0}^{1}$ $ϕ = \underset{n = 0}{\sum^{\infty}} \frac{1}{{(2 n + 2)}^{3}}$ $ϕ = \frac{1}{8} \underset{n = 0}{\sum^{\infty}} \frac{1}{{(n + 1)}^{3}}$ $ϕ = \frac{1}{8} \underset{n = 1}{\sum^{\infty}} \frac{1}{n^{3}}$ $ϕ = \frac{ζ (3)}{8}$
	Commented by mnjuly1970 last updated on 16/Dec/20

	$t h a n k s a l o t s i r o l a f . . .$
	Answered by Lordose last updated on 16/Dec/20

	$Ω = \int_{0}^{\frac{π}{2}} \frac{\sin (x) \ln (\sqrt{1 - \cos^{2} (x)}) \ln (\cos (x))}{\cos (x)} dx \overset{u = \cos (x)}{=} \int_{1}^{0} \frac{- \ln (\sqrt{1 - u^{2}}) \ln (u)}{u} du$ $Ω = \frac{1}{2} \int_{0}^{1} \frac{\ln (1 - u^{2}) \ln (u)}{u} du = \frac{1}{2} \int_{0}^{1} \frac{- \ln (u) \underset{n = 1}{\sum^{\infty}} \frac{u^{2 n}}{n}}{u} du$ $Ω = - \frac{1}{2} \underset{n = 1}{\sum^{\infty}} \frac{1}{n} \int_{0}^{1} u^{2 n - 1} \ln (u) du = - \frac{1}{2} \underset{n = 1}{\sum^{\infty}} \frac{1}{n} ∣ \frac{u^{2 n} (2 nlnu - 1)}{{4 n}^{2}} ∣_{0}^{1}$ $Ω = - \frac{1}{2} \underset{n = 1}{\sum^{\infty}} \frac{1}{n} \cdot - \frac{1}{{4 n}^{2}} = \frac{1}{8} \underset{n = 1}{\sum^{\infty}} \frac{1}{n^{3}} = \frac{ζ (3)}{8}$
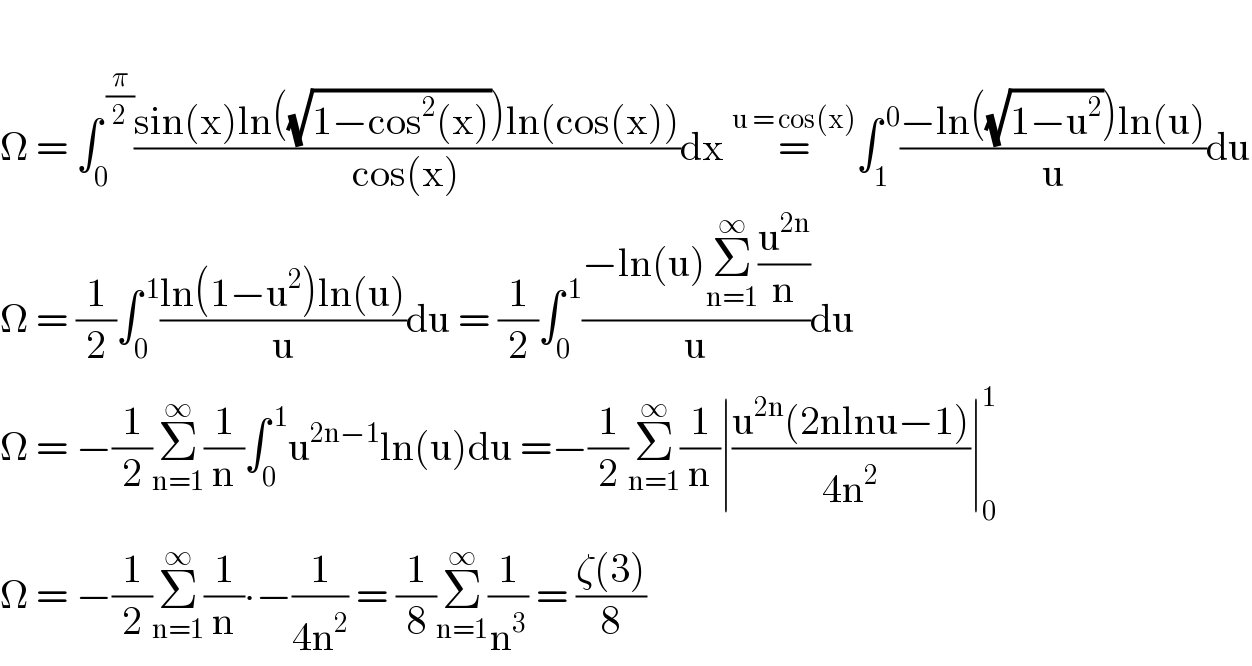
	Commented by mnjuly1970 last updated on 16/Dec/20

	$e x c e l l e n t s i r l o r d o s e . . .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum