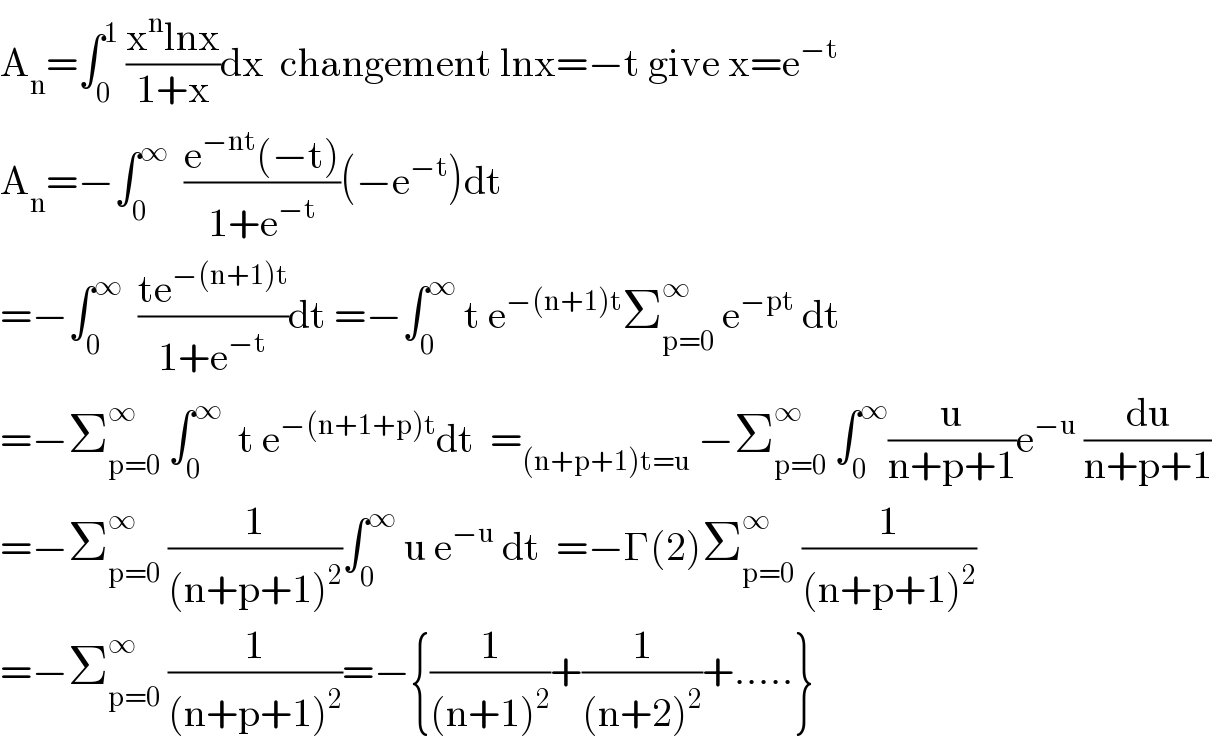Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 126139 by mnjuly1970 last updated on 17/Dec/20

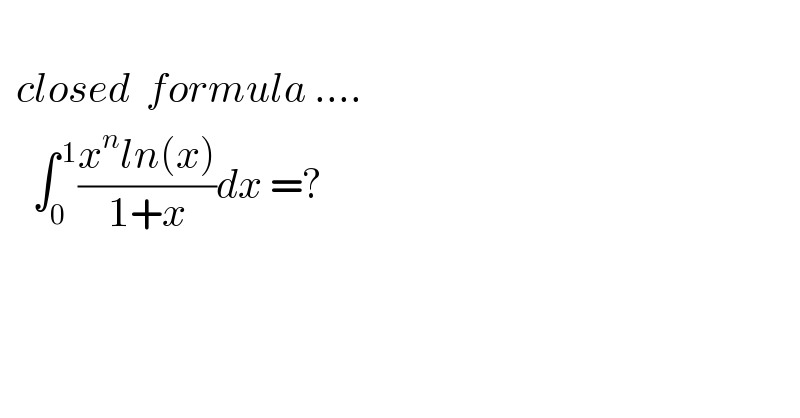
closed formula .... ∫_0 ^( 1) ((x^n ln(x))/(1+x))dx =?

$$\:\:\:\:\:\:\: \\ $$$$\:\:{closed}\:\:{formula}\:.... \\ $$$$\:\:\:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{x}^{{n}} {ln}\left({x}\right)}{\mathrm{1}+{x}}{dx}\:=? \\ $$$$\:\:\: \\ $$

Commented by Dwaipayan Shikari last updated on 17/Dec/20

Σ_(k=0) ^∞ (−1)^n ∫_0 ^1 x^n x^k log(x)dx =Σ_(k=0) ^∞ (−1)^k [log(x)(x^(n+k+1) /(n+k+1))]_0 ^1 −∫_0 ^1 (x^(n+k) /((n+k+1)))dx =Σ_(k=0) ^∞ (−1)^(k+1) (1/((n+k+1)^2 ))=−(1/((n+1+0)^2 ))+(1/((n+1+1)^2 ))−(1/((n+3)^2 ))+..=S (1/((n+1)^2 ))+(1/((n+2)^2 ))+(1/((n+3)^2 ))+..=ζ(2,n+1) S+ζ(2,n+1)=2((1/((n+2)^2 ))+(1/((n+4)^2 ))+....) S+ζ(2,n)=(1/2)Σ_(k=1) ^∞ (1/(((n/2)+k)^2 ))=(1/2)ζ(2,(n/2))−(2/n^2 ) S=(1/2)ζ(2,(n/2))−ζ(2,n+1)−(2/n^2 ) Note:Σ_(n=0) ^∞ (1/((n+k)^s ))=ζ(s,k) (Hurwitz zeta)

$$\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} {x}^{{k}} {log}\left({x}\right){dx} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{k}} \left[{log}\left({x}\right)\frac{{x}^{{n}+{k}+\mathrm{1}} }{{n}+{k}+\mathrm{1}}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{n}+{k}} }{\left({n}+{k}+\mathrm{1}\right)}{dx} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} \frac{\mathrm{1}}{\left({n}+{k}+\mathrm{1}\right)^{\mathrm{2}} }=−\frac{\mathrm{1}}{\left({n}+\mathrm{1}+\mathrm{0}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left({n}+\mathrm{1}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\left({n}+\mathrm{3}\right)^{\mathrm{2}} }+..={S} \\ $$$$\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left({n}+\mathrm{2}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left({n}+\mathrm{3}\right)^{\mathrm{2}} }+..=\zeta\left(\mathrm{2},{n}+\mathrm{1}\right) \\ $$$${S}+\zeta\left(\mathrm{2},{n}+\mathrm{1}\right)=\mathrm{2}\left(\frac{\mathrm{1}}{\left({n}+\mathrm{2}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left({n}+\mathrm{4}\right)^{\mathrm{2}} }+....\right) \\ $$$${S}+\zeta\left(\mathrm{2},{n}\right)=\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\frac{{n}}{\mathrm{2}}+{k}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}\zeta\left(\mathrm{2},\frac{{n}}{\mathrm{2}}\right)−\frac{\mathrm{2}}{{n}^{\mathrm{2}} } \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{2}}\zeta\left(\mathrm{2},\frac{{n}}{\mathrm{2}}\right)−\zeta\left(\mathrm{2},{n}+\mathrm{1}\right)−\frac{\mathrm{2}}{{n}^{\mathrm{2}} }\:\:\boldsymbol{{Note}}:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+{k}\right)^{{s}} }=\zeta\left({s},{k}\right)\:\left({Hurwitz}\:{zeta}\right) \\ $$

Commented by mnjuly1970 last updated on 17/Dec/20

thank you so much..

$${thank}\:\:{you}\:{so}\:{much}.. \\ $$

Commented by Dwaipayan Shikari last updated on 17/Dec/20

But the question seems to be deleted

$${But}\:{the}\:{question}\:{seems}\:{to}\:{be}\:{deleted} \\ $$

Commented by mnjuly1970 last updated on 17/Dec/20

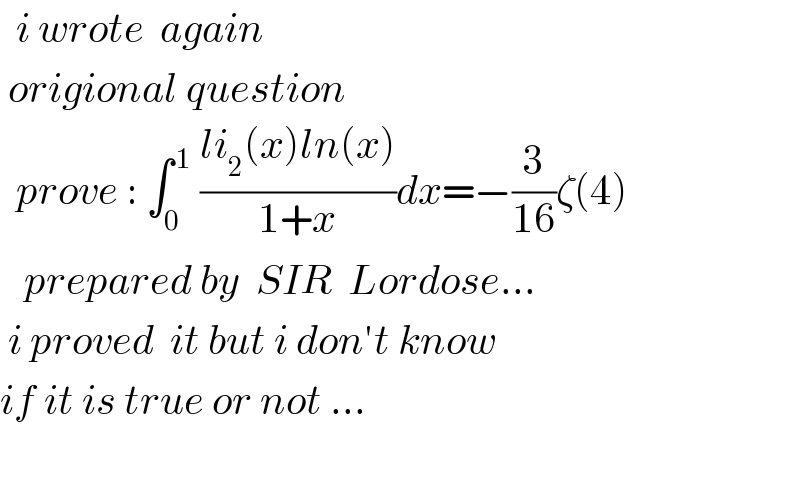
i wrote again origional question prove : ∫_0 ^( 1) ((li_2 (x)ln(x))/(1+x))dx=−(3/(16))ζ(4) prepared by SIR Lordose... i proved it but i don′t know if it is true or not ...

$$\:\:{i}\:{wrote}\:\:{again} \\ $$$$\:{origional}\:{question}\: \\ $$$$\:\:{prove}\::\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{{li}_{\mathrm{2}} \left({x}\right){ln}\left({x}\right)}{\mathrm{1}+{x}}{dx}=−\frac{\mathrm{3}}{\mathrm{16}}\zeta\left(\mathrm{4}\right) \\ $$$$\:\:\:{prepared}\:{by}\:\:{SIR}\:\:{Lordose}... \\ $$$$\:{i}\:{proved}\:\:{it}\:{but}\:{i}\:{don}'{t}\:{know} \\ $$$${if}\:{it}\:{is}\:{true}\:{or}\:{not}\:... \\ $$$$\: \\ $$

Answered by mathmax by abdo last updated on 17/Dec/20

A_n =∫_0 ^1 ((x^n lnx)/(1+x))dx changement lnx=−t give x=e^(−t) A_n =−∫_0 ^∞ ((e^(−nt) (−t))/(1+e^(−t) ))(−e^(−t) )dt =−∫_0 ^∞ ((te^(−(n+1)t) )/(1+e^(−t) ))dt =−∫_0 ^∞ t e^(−(n+1)t) Σ_(p=0) ^∞ e^(−pt) dt =−Σ_(p=0) ^∞ ∫_0 ^∞ t e^(−(n+1+p)t) dt =_((n+p+1)t=u) −Σ_(p=0) ^∞ ∫_0 ^∞ (u/(n+p+1))e^(−u) (du/(n+p+1)) =−Σ_(p=0) ^∞ (1/((n+p+1)^2 ))∫_0 ^∞ u e^(−u) dt =−Γ(2)Σ_(p=0) ^∞ (1/((n+p+1)^2 )) =−Σ_(p=0) ^∞ (1/((n+p+1)^2 ))=−{(1/((n+1)^2 ))+(1/((n+2)^2 ))+.....}

$$\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{n}} \mathrm{lnx}}{\mathrm{1}+\mathrm{x}}\mathrm{dx}\:\:\mathrm{changement}\:\mathrm{lnx}=−\mathrm{t}\:\mathrm{give}\:\mathrm{x}=\mathrm{e}^{−\mathrm{t}} \\ $$$$\mathrm{A}_{\mathrm{n}} =−\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{e}^{−\mathrm{nt}} \left(−\mathrm{t}\right)}{\mathrm{1}+\mathrm{e}^{−\mathrm{t}} }\left(−\mathrm{e}^{−\mathrm{t}} \right)\mathrm{dt} \\ $$$$=−\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{te}^{−\left(\mathrm{n}+\mathrm{1}\right)\mathrm{t}} }{\mathrm{1}+\mathrm{e}^{−\mathrm{t}} }\mathrm{dt}\:=−\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}\:\mathrm{e}^{−\left(\mathrm{n}+\mathrm{1}\right)\mathrm{t}} \sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{pt}} \:\mathrm{dt} \\ $$$$=−\sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \:\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{t}\:\mathrm{e}^{−\left(\mathrm{n}+\mathrm{1}+\mathrm{p}\right)\mathrm{t}} \mathrm{dt}\:\:=_{\left(\mathrm{n}+\mathrm{p}+\mathrm{1}\right)\mathrm{t}=\mathrm{u}} \:−\sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{u}}{\mathrm{n}+\mathrm{p}+\mathrm{1}}\mathrm{e}^{−\mathrm{u}} \:\frac{\mathrm{du}}{\mathrm{n}+\mathrm{p}+\mathrm{1}} \\ $$$$=−\sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{p}+\mathrm{1}\right)^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \:\mathrm{u}\:\mathrm{e}^{−\mathrm{u}} \:\mathrm{dt}\:\:=−\Gamma\left(\mathrm{2}\right)\sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{p}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=−\sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{p}+\mathrm{1}\right)^{\mathrm{2}} }=−\left\{\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{2}\right)^{\mathrm{2}} }+.....\right\} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com