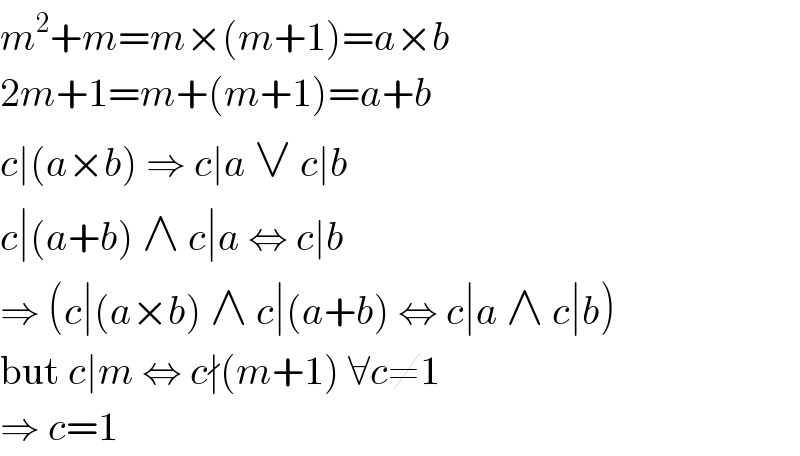show that m^2 +m and 2m+1 are prime betwen them.


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 126391 by mathocean1 last updated on 20/Dec/20

$s h o w t h a t$ $m^{2} + m a n d 2 m + 1 a r e p r i m e b e t w e n$ $t h e m .$
	Answered by akornes last updated on 20/Dec/20
	$for m ε Z^∗ −{−1} pgcd(m^2 +m ; 2m+1)=pgcd[m(m+1) ;m+(m+1)] =pgcd[m;(m+1)] =pgcd(m;1) =1 so m^2 +m and 2m+1 are prime betwen them$
	$f o r m ϵ Z^{*} - {- 1}$ $p g c d (m^{2} + m; 2 m + 1) = p g c d [m (m + 1); m + (m + 1)]$ $= p g c d [m; (m + 1)]$ $= p g c d (m; 1)$ $= 1 s o m^{2} + m a n d 2 m + 1 a r e p r i m e$ $b e t w e n t h e m$
	Commented by mathocean1 last updated on 20/Dec/20

	$t h a n k y o u a l l$
	Answered by mnjuly1970 last updated on 20/Dec/20
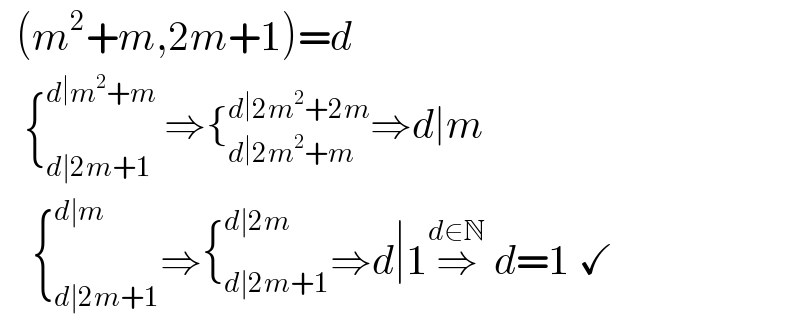
	$(m^2 +m,2m+1)=d {_(d∣2m+1) ^(d∣m^2 +m) ⇒{_(d∣2m^2 +m) ^(d∣2m^2 +2m) ⇒d∣m {_(d∣2m+1) ^(d∣m) ⇒{_(d∣2m+1) ^(d∣2m) ⇒d∣1⇒^(d∈N) d=1 ✓$
	$(m^{2} + m, 2 m + 1) = d$ ${_{d ∣ 2 m + 1}^{d ∣ m^{2} + m} \Rightarrow {_{d ∣ 2 m^{2} + m}^{d ∣ 2 m^{2} + 2 m} \Rightarrow d ∣ m$ ${_{d ∣ 2 m + 1}^{d ∣ m} \Rightarrow {_{d ∣ 2 m + 1}^{d ∣ 2 m} \Rightarrow d ∣ 1 \overset{d \in N}{\Rightarrow} d = 1 ✓$
	Answered by MJS_new last updated on 20/Dec/20

	$m^{2} + m = m \times (m + 1) = a \times b$ $2 m + 1 = m + (m + 1) = a + b$ $c ∣ (a \times b) \Rightarrow c ∣ a \lor c ∣ b$ $c ∣ (a + b) \land c ∣ a \Leftrightarrow c ∣ b$ $\Rightarrow (c ∣ (a \times b) \land c ∣ (a + b) \Leftrightarrow c ∣ a \land c ∣ b)$ $but c ∣ m \Leftrightarrow c ∤ (m + 1) \forall c \neq 1$ $\Rightarrow c = 1$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum