Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 126476 by mnjuly1970 last updated on 20/Dec/20

...nice calculus... calculate :: Ω=∫_0 ^( ∞) ((tanh(πx))/(x(1+x^2 ))) dx=?

$$\:\:\:\:\:\:\:\:...{nice}\:\:{calculus}... \\ $$$$\:\:{calculate}\::: \\ $$$$\:\:\:\:\:\:\Omega=\int_{\mathrm{0}} ^{\:\infty} \:\frac{{tanh}\left(\pi{x}\right)}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\:{dx}=? \\ $$

Answered by mathmax by abdo last updated on 21/Dec/20

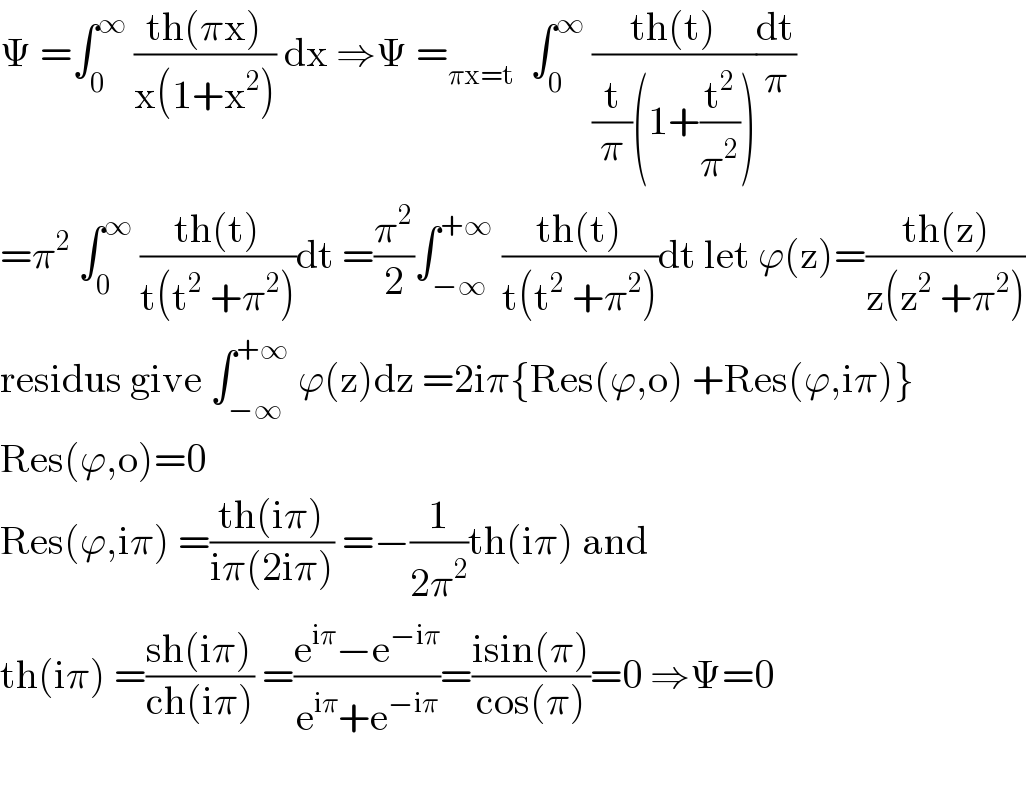
Ψ =∫_0 ^∞ ((th(πx))/(x(1+x^2 ))) dx ⇒Ψ =_(πx=t) ∫_0 ^∞ ((th(t))/((t/π)(1+(t^2 /π^2 ))))(dt/π) =π^2 ∫_0 ^∞ ((th(t))/(t(t^2 +π^2 )))dt =(π^2 /2)∫_(−∞) ^(+∞) ((th(t))/(t(t^2 +π^2 )))dt let ϕ(z)=((th(z))/(z(z^2 +π^2 ))) residus give ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{Res(ϕ,o) +Res(ϕ,iπ)} Res(ϕ,o)=0 Res(ϕ,iπ) =((th(iπ))/(iπ(2iπ))) =−(1/(2π^2 ))th(iπ) and th(iπ) =((sh(iπ))/(ch(iπ))) =((e^(iπ) −e^(−iπ) )/(e^(iπ) +e^(−iπ) ))=((isin(π))/(cos(π)))=0 ⇒Ψ=0

$$\Psi\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{th}\left(\pi\mathrm{x}\right)}{\mathrm{x}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}\:\mathrm{dx}\:\Rightarrow\Psi\:=_{\pi\mathrm{x}=\mathrm{t}} \:\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{th}\left(\mathrm{t}\right)}{\frac{\mathrm{t}}{\pi}\left(\mathrm{1}+\frac{\mathrm{t}^{\mathrm{2}} }{\pi^{\mathrm{2}} }\right)}\frac{\mathrm{dt}}{\pi} \\ $$$$=\pi^{\mathrm{2}} \:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{th}\left(\mathrm{t}\right)}{\mathrm{t}\left(\mathrm{t}^{\mathrm{2}} \:+\pi^{\mathrm{2}} \right)}\mathrm{dt}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{2}}\int_{−\infty} ^{+\infty} \:\frac{\mathrm{th}\left(\mathrm{t}\right)}{\mathrm{t}\left(\mathrm{t}^{\mathrm{2}} \:+\pi^{\mathrm{2}} \right)}\mathrm{dt}\:\mathrm{let}\:\varphi\left(\mathrm{z}\right)=\frac{\mathrm{th}\left(\mathrm{z}\right)}{\mathrm{z}\left(\mathrm{z}^{\mathrm{2}} \:+\pi^{\mathrm{2}} \right)} \\ $$$$\mathrm{residus}\:\mathrm{give}\:\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\left\{\mathrm{Res}\left(\varphi,\mathrm{o}\right)\:+\mathrm{Res}\left(\varphi,\mathrm{i}\pi\right)\right\} \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{o}\right)=\mathrm{0} \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{i}\pi\right)\:=\frac{\mathrm{th}\left(\mathrm{i}\pi\right)}{\mathrm{i}\pi\left(\mathrm{2i}\pi\right)}\:=−\frac{\mathrm{1}}{\mathrm{2}\pi^{\mathrm{2}} }\mathrm{th}\left(\mathrm{i}\pi\right)\:\mathrm{and} \\ $$$$\mathrm{th}\left(\mathrm{i}\pi\right)\:=\frac{\mathrm{sh}\left(\mathrm{i}\pi\right)}{\mathrm{ch}\left(\mathrm{i}\pi\right)}\:=\frac{\mathrm{e}^{\mathrm{i}\pi} −\mathrm{e}^{−\mathrm{i}\pi} }{\mathrm{e}^{\mathrm{i}\pi} +\mathrm{e}^{−\mathrm{i}\pi} }=\frac{\mathrm{isin}\left(\pi\right)}{\mathrm{cos}\left(\pi\right)}=\mathrm{0}\:\Rightarrow\Psi=\mathrm{0} \\ $$$$ \\ $$

Answered by mathmax by abdo last updated on 21/Dec/20

if you have another way post it sir mnj

$$\mathrm{if}\:\mathrm{you}\:\mathrm{have}\:\mathrm{another}\:\mathrm{way}\:\mathrm{post}\:\mathrm{it}\:\mathrm{sir}\:\mathrm{mnj} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com