Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 126682 by bramlexs22 last updated on 23/Dec/20

Find the remainder 7+77+777+7777+...+777...7_(2020 times) when divided by 9.

$$\:{Find}\:{the}\:{remainder}\: \\ $$$$\:\mathrm{7}+\mathrm{77}+\mathrm{777}+\mathrm{7777}+...+\underset{\mathrm{2020}\:{times}} {\underbrace{\mathrm{777}...\mathrm{7}}} \\ $$$${when}\:{divided}\:{by}\:\mathrm{9}. \\ $$

Answered by talminator2856791 last updated on 23/Dec/20

7Σ_(k=1) ^(2020) k(10^(2020−k) ) = 7Σ_(k=1) ^(2020) Σ_(i=1) ^k 10^(i−1) 10^n ≡ 1 mod 9 , n ∈ N ⇒ ((7Σ_(k=1) ^(2020) Σ_(i=1) ^k 10^(i−1) )/9) = 9j + 7(2020)+ 7Σ_(k=1) ^(2019) k = 9j + 14140 + 7(2019)(1010) = 9j + 14 288 470 ((14 288 470)/9) = 1 587 607.7777..... ⇒ 7+77+777+.......+777...7_(2020 times) has remainder of 7 when divided by 9

$$\: \\ $$$$\:\mathrm{7}\underset{{k}=\mathrm{1}} {\overset{\mathrm{2020}} {\sum}}\:{k}\left(\mathrm{10}^{\mathrm{2020}−{k}} \right)\:=\:\mathrm{7}\underset{{k}=\mathrm{1}} {\overset{\mathrm{2020}} {\sum}}\underset{{i}=\mathrm{1}} {\overset{{k}} {\sum}}\:\mathrm{10}^{{i}−\mathrm{1}} \\ $$$$\: \\ $$$$\:\mathrm{10}^{{n}} \:\equiv\:\mathrm{1}\:\mathrm{mod}\:\mathrm{9}\:,\:\:{n}\:\in\:\mathbb{N} \\ $$$$\: \\ $$$$\:\Rightarrow\:\frac{\mathrm{7}\underset{{k}=\mathrm{1}} {\overset{\mathrm{2020}} {\sum}}\underset{{i}=\mathrm{1}} {\overset{{k}} {\sum}}\:\mathrm{10}^{{i}−\mathrm{1}} }{\mathrm{9}}\:=\:\mathrm{9}{j}\:+\:\mathrm{7}\left(\mathrm{2020}\right)+\:\mathrm{7}\underset{{k}=\mathrm{1}} {\overset{\mathrm{2019}} {\sum}}{k}\: \\ $$$$\:\:\:\:\:\:\:=\:\mathrm{9}{j}\:+\:\mathrm{14140}\:+\:\mathrm{7}\left(\mathrm{2019}\right)\left(\mathrm{1010}\right) \\ $$$$\:\:\:\:\:\:\:=\:\mathrm{9}{j}\:+\:\mathrm{14}\:\mathrm{288}\:\mathrm{470}\: \\ $$$$\: \\ $$$$\:\frac{\mathrm{14}\:\mathrm{288}\:\mathrm{470}}{\mathrm{9}}\:=\:\mathrm{1}\:\mathrm{587}\:\mathrm{607}.\mathrm{7777}..... \\ $$$$\: \\ $$$$\:\Rightarrow\:\mathrm{7}+\mathrm{77}+\mathrm{777}+.......+\underset{\mathrm{2020}\:\mathrm{times}} {\underbrace{\mathrm{777}...\mathrm{7}}}\:\: \\ $$$$\:\:\:\:\:\:\:\:\mathrm{has}\:\mathrm{remainder}\:\mathrm{of}\:\mathrm{7}\:\mathrm{when}\:\mathrm{divided}\:\mathrm{by}\:\mathrm{9} \\ $$$$\: \\ $$

Answered by floor(10²Eta[1]) last updated on 23/Dec/20

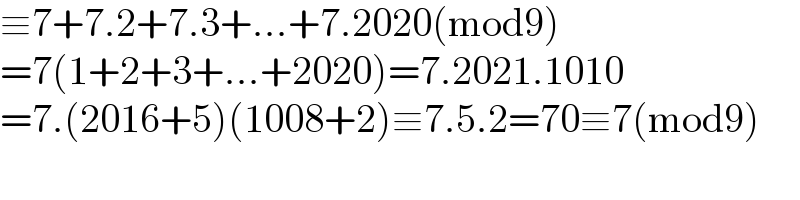
≡7+7.2+7.3+...+7.2020(mod9) =7(1+2+3+...+2020)=7.2021.1010 =7.(2016+5)(1008+2)≡7.5.2=70≡7(mod9)

$$\equiv\mathrm{7}+\mathrm{7}.\mathrm{2}+\mathrm{7}.\mathrm{3}+...+\mathrm{7}.\mathrm{2020}\left(\mathrm{mod9}\right) \\ $$$$=\mathrm{7}\left(\mathrm{1}+\mathrm{2}+\mathrm{3}+...+\mathrm{2020}\right)=\mathrm{7}.\mathrm{2021}.\mathrm{1010} \\ $$$$=\mathrm{7}.\left(\mathrm{2016}+\mathrm{5}\right)\left(\mathrm{1008}+\mathrm{2}\right)\equiv\mathrm{7}.\mathrm{5}.\mathrm{2}=\mathrm{70}\equiv\mathrm{7}\left(\mathrm{mod9}\right) \\ $$

Commented by talminator2856791 last updated on 24/Dec/20

how can you say ≡7+7.2+7.3+...+7.2020(mod9)?

$$\:\mathrm{how}\:\mathrm{can}\:\mathrm{you}\:\mathrm{say} \\ $$$$\:\equiv\mathrm{7}+\mathrm{7}.\mathrm{2}+\mathrm{7}.\mathrm{3}+...+\mathrm{7}.\mathrm{2020}\left(\mathrm{mod9}\right)? \\ $$$$\: \\ $$

Commented by floor(10²Eta[1]) last updated on 24/Dec/20

a_n 10^n +a_(n−1) 10^(n−1) +...+a_1 10+a_0 ≡a_n +a_(n−1) +...+a_1 +a_0 (mod 9) so 77≡7+7=7.2(mod 9) because 77=7.10+7 and so on...

$$\mathrm{a}_{\mathrm{n}} \mathrm{10}^{\mathrm{n}} +\mathrm{a}_{\mathrm{n}−\mathrm{1}} \mathrm{10}^{\mathrm{n}−\mathrm{1}} +...+\mathrm{a}_{\mathrm{1}} \mathrm{10}+\mathrm{a}_{\mathrm{0}} \\ $$$$\equiv\mathrm{a}_{\mathrm{n}} +\mathrm{a}_{\mathrm{n}−\mathrm{1}} +...+\mathrm{a}_{\mathrm{1}} +\mathrm{a}_{\mathrm{0}} \left(\mathrm{mod}\:\mathrm{9}\right) \\ $$$$\mathrm{so}\:\mathrm{77}\equiv\mathrm{7}+\mathrm{7}=\mathrm{7}.\mathrm{2}\left(\mathrm{mod}\:\mathrm{9}\right)\:\mathrm{because}\:\mathrm{77}=\mathrm{7}.\mathrm{10}+\mathrm{7} \\ $$$$\mathrm{and}\:\mathrm{so}\:\mathrm{on}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com