
Question Number 126865 by Lordose last updated on 24/Dec/20

$$\int_{\mathrm{0}} ^{\:\pi} \frac{\mathrm{x}}{\mathrm{2}+\mathrm{cos}\left(\mathrm{2x}\right)}\mathrm{dx}\:=\:\mathrm{0} \\ $$$$\mathrm{Prove}\:\mathrm{or}\:\mathrm{Disprove} \\ $$
Commented by Ar Brandon last updated on 25/Dec/20

Commented by bramlexs22 last updated on 25/Dec/20

Commented by liberty last updated on 25/Dec/20

Commented by MJS_new last updated on 25/Dec/20
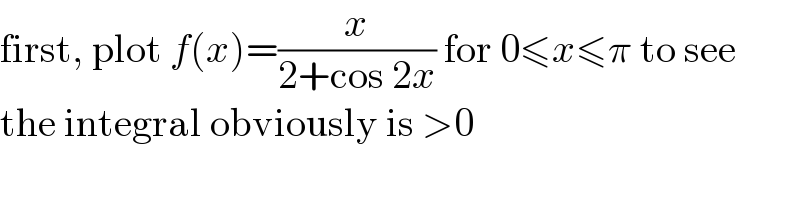
$$\mathrm{first},\:\mathrm{plot}\:{f}\left({x}\right)=\frac{{x}}{\mathrm{2}+\mathrm{cos}\:\mathrm{2}{x}}\:\mathrm{for}\:\mathrm{0}\leqslant{x}\leqslant\pi\:\mathrm{to}\:\mathrm{see} \\ $$$$\mathrm{the}\:\mathrm{integral}\:\mathrm{obviously}\:\mathrm{is}\:>\mathrm{0} \\ $$
Answered by Ar Brandon last updated on 25/Dec/20
![I=∫_0 ^π (x/(2+cos(2x)))dx I=∫_0 ^π ((π−x)/(2+cos(2π−2x)))dx=∫_0 ^π ((π−x)/(2+cos(2x)))dx 2I=∫_0 ^π (π/(2+cos(2x)))dx=∫_0 ^π (π/(1+2cos^2 x))dx =∫_0 ^π ((πsec^2 x)/(sec^2 x+2))dx=∫_0 ^π ((πd(tanx))/(3+tan^2 x)) =π[(1/( (√3)))Arctan(((tanx)/( (√3))))]_0 ^π =(π^2 /( (√3))) I=(π^2 /( 2(√3)))≈2.849109379](Q126866.png)
$$\mathcal{I}=\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{x}}{\mathrm{2}+\mathrm{cos}\left(\mathrm{2x}\right)}\mathrm{dx} \\ $$$$\mathcal{I}=\int_{\mathrm{0}} ^{\pi} \frac{\pi−\mathrm{x}}{\mathrm{2}+\mathrm{cos}\left(\mathrm{2}\pi−\mathrm{2x}\right)}\mathrm{dx}=\int_{\mathrm{0}} ^{\pi} \frac{\pi−\mathrm{x}}{\mathrm{2}+\mathrm{cos}\left(\mathrm{2x}\right)}\mathrm{dx} \\ $$$$\mathrm{2}\mathcal{I}=\int_{\mathrm{0}} ^{\pi} \frac{\pi}{\mathrm{2}+\mathrm{cos}\left(\mathrm{2x}\right)}\mathrm{dx}=\int_{\mathrm{0}} ^{\pi} \frac{\pi}{\mathrm{1}+\mathrm{2cos}^{\mathrm{2}} \mathrm{x}}\mathrm{dx} \\ $$$$\:\:\:\:\:\:=\int_{\mathrm{0}} ^{\pi} \frac{\pi\mathrm{sec}^{\mathrm{2}} \mathrm{x}}{\mathrm{sec}^{\mathrm{2}} \mathrm{x}+\mathrm{2}}\mathrm{dx}=\int_{\mathrm{0}} ^{\pi} \frac{\pi\mathrm{d}\left(\mathrm{tanx}\right)}{\mathrm{3}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}} \\ $$$$\:\:\:\:\:\:=\pi\left[\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{Arctan}\left(\frac{\mathrm{tanx}}{\:\sqrt{\mathrm{3}}}\right)\right]_{\mathrm{0}} ^{\pi} =\frac{\pi^{\mathrm{2}} }{\:\sqrt{\mathrm{3}}} \\ $$$$\mathcal{I}=\frac{\pi^{\mathrm{2}} }{\:\mathrm{2}\sqrt{\mathrm{3}}}\approx\mathrm{2}.\mathrm{849109379} \\ $$
Commented by Lordose last updated on 25/Dec/20

$$\mathrm{tan}\left(\pi\right)\:=\:\mathrm{0}\:\mathrm{bro} \\ $$
Commented by Ar Brandon last updated on 25/Dec/20

$$\mathrm{I}\:\mathrm{realized}\:\mathrm{sometime}\:\mathrm{ago}\:\mathrm{that}\:\mathrm{when}\:\mathrm{dealing}\:\mathrm{with} \\ $$$$\mathrm{Arctan}\left(\frac{\mathrm{tan}\left(\mathrm{x}\right)}{\mathrm{a}}\right)\:\mathrm{we}'\mathrm{ve}\:\mathrm{got}\:\mathrm{to}\:\mathrm{make}\:\mathrm{use}\:\mathrm{of}\:\mathrm{the}\:\mathrm{sign}\:\mathrm{on}\:\mathrm{zero}. \\ $$$$\mathrm{That}\:\mathrm{is}\:\mathrm{tan0}=\frac{\mathrm{sin0}}{\mathrm{cos0}}=\frac{\mathrm{0}}{+\mathrm{1}}=+\mathrm{0}\:\Rightarrow\mathrm{Arctan}\left(\frac{\mathrm{tan0}}{\mathrm{a}}\right)=\mathrm{Arctan}\left(+\mathrm{0}\right)=\mathrm{0} \\ $$$$\mathrm{And}\:\mathrm{same}\:\mathrm{goes}\:\mathrm{for}\:\mathrm{tan}\pi \\ $$$$\mathrm{tan}\pi=\frac{\mathrm{sin}\pi}{\mathrm{cos}\pi}=\frac{\mathrm{0}}{−\mathrm{1}}=−\mathrm{0}\:\mathrm{then}\:\mathrm{Arctan}\left(\frac{\mathrm{tan}\pi}{\mathrm{a}}\right)=\mathrm{Arctan}\left(−\mathrm{0}\right)=\pi \\ $$$$\mathrm{That}'\mathrm{s}\:\mathrm{why}\:\mathrm{my}\:\mathrm{answer}\:\mathrm{corresponds}\:\mathrm{with}\:\mathrm{that}\:\mathrm{obtained}\:\mathrm{using}\: \\ $$$$\mathrm{the}\:\mathrm{scientific}\:\mathrm{calculator}.\:\mathrm{Perhabs}\:\mathrm{someone}\:\mathrm{may}\:\mathrm{have}\:\mathrm{a} \\ $$$$\mathrm{better}\:\mathrm{explanation}\:\mathrm{for}\:\mathrm{this}\:\mathrm{result}. \\ $$
Commented by MJS_new last updated on 25/Dec/20
![the function f(x)=(π/(2+cos 2x)) obviously is symmetric to x=(π/2) ⇒ I=π∫_0 ^(π/2) (dx/(2+cos 2x))= [t=tan x → dx=cos^2 x dt] =π∫_0 ^∞ (dt/(t^2 +3))=((π(√3))/3)[arctan (t/( (√3)))]_0 ^∞ =((π^2 (√3))/6)≈2.84911](Q126982.png)
$$\mathrm{the}\:\mathrm{function}\:{f}\left({x}\right)=\frac{\pi}{\mathrm{2}+\mathrm{cos}\:\mathrm{2}{x}}\:\mathrm{obviously}\:\mathrm{is} \\ $$$$\mathrm{symmetric}\:\mathrm{to}\:{x}=\frac{\pi}{\mathrm{2}}\:\Rightarrow\: \\ $$$${I}=\pi\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{{dx}}{\mathrm{2}+\mathrm{cos}\:\mathrm{2}{x}}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:{x}\:\rightarrow\:{dx}=\mathrm{cos}^{\mathrm{2}} \:{x}\:{dt}\right] \\ $$$$=\pi\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{3}}=\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{3}}\left[\mathrm{arctan}\:\frac{{t}}{\:\sqrt{\mathrm{3}}}\right]_{\mathrm{0}} ^{\infty} =\frac{\pi^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{6}}\approx\mathrm{2}.\mathrm{84911} \\ $$
Commented by MJS_new last updated on 25/Dec/20
![...if the borders change from [a, b] to [c, c] you always have to look for symmetry. that is the point](Q126984.png)
$$...\mathrm{if}\:\mathrm{the}\:\mathrm{borders}\:\mathrm{change}\:\mathrm{from}\:\left[{a},\:{b}\right]\:\mathrm{to}\:\left[{c},\:{c}\right] \\ $$$$\mathrm{you}\:\mathrm{always}\:\mathrm{have}\:\mathrm{to}\:\mathrm{look}\:\mathrm{for}\:\mathrm{symmetry}.\:\mathrm{that} \\ $$$$\mathrm{is}\:\mathrm{the}\:\mathrm{point} \\ $$
Commented by Ar Brandon last updated on 26/Dec/20
Sounds better as an explanation.
Commented by Ar Brandon last updated on 26/Dec/20
Back from feast ? Haha !
Answered by Olaf last updated on 25/Dec/20
![Ω = ∫_0 ^π (x/(2+cos(2x)))dx (1) Let u = π−x 2Ω = ∫_π ^0 ((π−u)/(2+cos(2u)))(−du) = ∫_0 ^π ((π−u)/(2+cos(2u)))du (2) (1)+(2) : 2Ω = ∫_0 ^π (π/(2+cos(2x)))dx 2Ω = ∫_0 ^π (π/(2+((1−tan^2 x)/(1+tan^2 x))))dx 2Ω = ∫_0 ^π (π/(3−tan^2 x))(1+tan^2 x)dx 2Ω = ∫_0 ^(π/2) + ∫_(π/2) ^π = Ω_1 +Ω_2 Let v = tanx Ω_1 = π∫_0 ^∞ (dv/(3−v^2 )) Ω_1 = (π/(2(√3)))∫_0 ^∞ [(1/( (√3)+v))+(1/( (√3)−v))]dv Ω_1 = (π/(2(√3)))∫_0 ^∞ [ln∣(((√3)+v)/( (√3)−v))∣]_0 ^∞ = 0 ...and Ω_2 = 0 ⇒ Ω = 0](Q126867.png)
$$\Omega\:=\:\int_{\mathrm{0}} ^{\pi} \frac{{x}}{\mathrm{2}+\mathrm{cos}\left(\mathrm{2}{x}\right)}{dx}\:\left(\mathrm{1}\right) \\ $$$$\mathrm{Let}\:{u}\:=\:\pi−{x} \\ $$$$\mathrm{2}\Omega\:=\:\int_{\pi} ^{\mathrm{0}} \frac{\pi−{u}}{\mathrm{2}+\mathrm{cos}\left(\mathrm{2}{u}\right)}\left(−{du}\right)\:=\:\int_{\mathrm{0}} ^{\pi} \frac{\pi−{u}}{\mathrm{2}+\mathrm{cos}\left(\mathrm{2}{u}\right)}{du}\:\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)+\left(\mathrm{2}\right)\:: \\ $$$$\mathrm{2}\Omega\:=\:\int_{\mathrm{0}} ^{\pi} \frac{\pi}{\mathrm{2}+\mathrm{cos}\left(\mathrm{2}{x}\right)}{dx} \\ $$$$\mathrm{2}\Omega\:=\:\int_{\mathrm{0}} ^{\pi} \frac{\pi}{\mathrm{2}+\frac{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} {x}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} {x}}}{dx} \\ $$$$\mathrm{2}\Omega\:=\:\int_{\mathrm{0}} ^{\pi} \frac{\pi}{\mathrm{3}−\mathrm{tan}^{\mathrm{2}} {x}}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} {x}\right){dx} \\ $$$$\mathrm{2}\Omega\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} +\:\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} \:=\:\Omega_{\mathrm{1}} +\Omega_{\mathrm{2}} \\ $$$$\mathrm{Let}\:{v}\:=\:\mathrm{tan}{x} \\ $$$$\Omega_{\mathrm{1}} \:=\:\pi\int_{\mathrm{0}} ^{\infty} \frac{{dv}}{\mathrm{3}−{v}^{\mathrm{2}} } \\ $$$$\Omega_{\mathrm{1}} \:=\:\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}\int_{\mathrm{0}} ^{\infty} \left[\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}+{v}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}−{v}}\right]{dv} \\ $$$$\Omega_{\mathrm{1}} \:=\:\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}\int_{\mathrm{0}} ^{\infty} \left[\mathrm{ln}\mid\frac{\sqrt{\mathrm{3}}+{v}}{\:\sqrt{\mathrm{3}}−{v}}\mid\right]_{\mathrm{0}} ^{\infty} =\:\mathrm{0} \\ $$$$...\mathrm{and}\:\Omega_{\mathrm{2}} \:=\:\mathrm{0} \\ $$$$\Rightarrow\:\Omega\:=\:\mathrm{0} \\ $$
Commented by MJS_new last updated on 25/Dec/20

$$\mathrm{sorry}\:\mathrm{but}\:\mathrm{you}'\mathrm{re}\:\mathrm{wrong} \\ $$
