Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 126960 by bramlexs22 last updated on 25/Dec/20

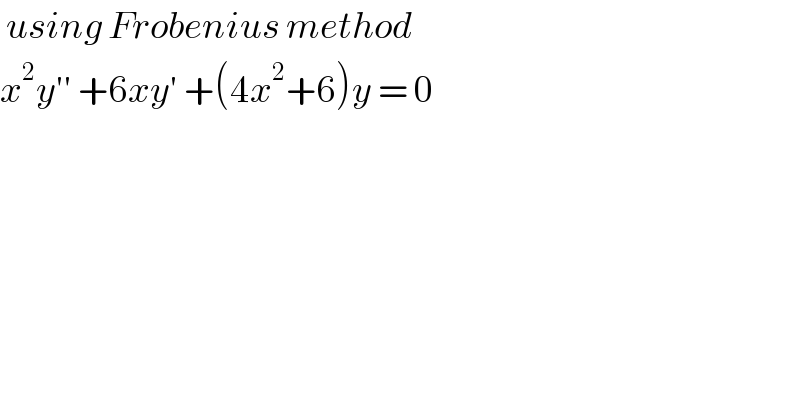
using Frobenius method x^2 y′′ +6xy′ +(4x^2 +6)y = 0

$$\:{using}\:{Frobenius}\:{method} \\ $$$${x}^{\mathrm{2}} {y}''\:+\mathrm{6}{xy}'\:+\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{6}\right){y}\:=\:\mathrm{0} \\ $$

Commented by liberty last updated on 26/Dec/20

put y=e^(rx) → { ((y′=re^(rx) )),((y′′=r^2 e^(rx) )) :} ⇔ x^2 (r^2 e^(rx) )+ 6x(r e^(rx) )+(4x^2 +6)e^(rx) = 0 ⇔ e^(rx) (x^2 r^2 +6xr +(4x^2 +6)) = 0 ⇒ x^2 r^2 + 6xr + (4x^2 +6) = 0 r = ((−6x±(√(36x^2 −4x^2 (4x^2 +6))))/(2x^2 )) r= ((−6x ± 2x(√(3−4x^2 )))/(2x^2 )) = ((−3±(√(3−4x^2 )))/x) r_1 =((−3+(√(3−4x^2 )))/x) ∧ r_2 = ((−3−(√(3−4x^2 )))/x) general solution ∴ y = C_1 e^(−3+(√(3−4x^2 ))) + C_2 e^(−3−(√(3−4x^2 ))) .

$${put}\:{y}={e}^{{rx}} \:\rightarrow\begin{cases}{{y}'={re}^{{rx}} }\\{{y}''={r}^{\mathrm{2}} {e}^{{rx}} }\end{cases} \\ $$$$\Leftrightarrow\:{x}^{\mathrm{2}} \left({r}^{\mathrm{2}} \:{e}^{{rx}} \:\right)+\:\mathrm{6}{x}\left({r}\:{e}^{{rx}} \right)+\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{6}\right){e}^{{rx}} \:=\:\mathrm{0} \\ $$$$\Leftrightarrow\:{e}^{{rx}} \:\left({x}^{\mathrm{2}} {r}^{\mathrm{2}} \:+\mathrm{6}{xr}\:+\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{6}\right)\right)\:=\:\mathrm{0} \\ $$$$\Rightarrow\:{x}^{\mathrm{2}} \:{r}^{\mathrm{2}} \:+\:\mathrm{6}{xr}\:+\:\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{6}\right)\:=\:\mathrm{0} \\ $$$$\:\:\:\:\:\:{r}\:=\:\frac{−\mathrm{6}{x}\pm\sqrt{\mathrm{36}{x}^{\mathrm{2}} −\mathrm{4}{x}^{\mathrm{2}} \left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{6}\right)}}{\mathrm{2}{x}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:{r}=\:\frac{−\mathrm{6}{x}\:\pm\:\mathrm{2}{x}\sqrt{\mathrm{3}−\mathrm{4}{x}^{\mathrm{2}} }}{\mathrm{2}{x}^{\mathrm{2}} }\:=\:\frac{−\mathrm{3}\pm\sqrt{\mathrm{3}−\mathrm{4}{x}^{\mathrm{2}} }}{{x}} \\ $$$$\:\:\:\:\:{r}_{\mathrm{1}} =\frac{−\mathrm{3}+\sqrt{\mathrm{3}−\mathrm{4}{x}^{\mathrm{2}} }}{{x}}\:\wedge\:{r}_{\mathrm{2}} =\:\frac{−\mathrm{3}−\sqrt{\mathrm{3}−\mathrm{4}{x}^{\mathrm{2}} }}{{x}} \\ $$$${general}\:{solution} \\ $$$$\:\therefore\:{y}\:=\:{C}_{\mathrm{1}} {e}^{−\mathrm{3}+\sqrt{\mathrm{3}−\mathrm{4}{x}^{\mathrm{2}} }} \:+\:{C}_{\mathrm{2}} {e}^{−\mathrm{3}−\sqrt{\mathrm{3}−\mathrm{4}{x}^{\mathrm{2}} }} \:.\: \\ $$

Commented by bramlexs22 last updated on 26/Dec/20

yes..thanks

$${yes}..{thanks}\: \\ $$

Answered by Dwaipayan Shikari last updated on 26/Dec/20

y=e^(λx) λ^2 x^2 e^(λx) +6λe^(λx) +(4x^2 +6)e^(λx) =0 ⇒λ^2 x^2 +6λx+4x^2 +6=0⇒λ=((−6x±(√(36x^2 −16x^4 −24x^2 )))/(2x^2 )) λ=−(3/x)±(√((3/x^2 )−4)) y=Λe^(−(3/x)+(√((3/x^2 )−4))) +Φe^(−(3/x)−(√((3/x^2 )−4)))

$${y}={e}^{\lambda{x}} \\ $$$$\lambda^{\mathrm{2}} {x}^{\mathrm{2}} {e}^{\lambda{x}} +\mathrm{6}\lambda{e}^{\lambda{x}} +\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{6}\right){e}^{\lambda{x}} =\mathrm{0} \\ $$$$\Rightarrow\lambda^{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{6}\lambda{x}+\mathrm{4}{x}^{\mathrm{2}} +\mathrm{6}=\mathrm{0}\Rightarrow\lambda=\frac{−\mathrm{6}{x}\pm\sqrt{\mathrm{36}{x}^{\mathrm{2}} −\mathrm{16}{x}^{\mathrm{4}} −\mathrm{24}{x}^{\mathrm{2}} }}{\mathrm{2}{x}^{\mathrm{2}} } \\ $$$$\lambda=−\frac{\mathrm{3}}{{x}}\pm\sqrt{\frac{\mathrm{3}}{{x}^{\mathrm{2}} }−\mathrm{4}} \\ $$$${y}=\Lambda{e}^{−\frac{\mathrm{3}}{{x}}+\sqrt{\frac{\mathrm{3}}{{x}^{\mathrm{2}} }−\mathrm{4}}} +\Phi{e}^{−\frac{\mathrm{3}}{{x}}−\sqrt{\frac{\mathrm{3}}{{x}^{\mathrm{2}} }−\mathrm{4}}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com