
Question and Answers Forum
Question Number 127017 by mnjuly1970 last updated on 26/Dec/20
![...NICE CALCULUS... prove that :: ∫_0 ^( ∞) (((x^2 ln(πx))/π^(πx) ))dx =(1/((πln(π))^3 ))[(3−2(γ+ln(ln(π)))]](Q127017.png)
Answered by mindispower last updated on 26/Dec/20
![=∫_0 ^∞ x^2 ln(πx)e^(−πxln(π)) dx u=πln(π)x ⇒dx=(du/(πln(π))) ⇔∫_0 ^∞ (u^2 /(π^2 ln^2 (π)))ln((u/(ln(π))))e^(−u) .(du/(πln(π))) =(1/(π^3 ln^3 (π)))[∫_0 ^∞ u^2 ln(u)e^(−u) du−ln(lnπ)∫_0 ^∞ u^2 e^(−u) ] =(1/(π^3 ln^3 (π))){Γ′(3)−ln(ln(π).Γ(3)} =((Γ(3).Ψ(3))/(π^3 ln^3 (π)))−(1/(π^3 ln^3 (π)))2ln(lnπ) =2((1/2)+1−γ).(1/(π^3 ln^3 (π)))−((2ln(lnπ))/(π^3 ln^3 (π))) =((3−2γ)/(π^3 ln^3 (π)))−((2ln(lnπ))/(π^3 ln^3 (π)))=(1/((πlnπ)^3 ))[(3−2(γ+ln(lnπ))]](Q127019.png)
Commented by mnjuly1970 last updated on 26/Dec/20

Answered by Dwaipayan Shikari last updated on 26/Dec/20
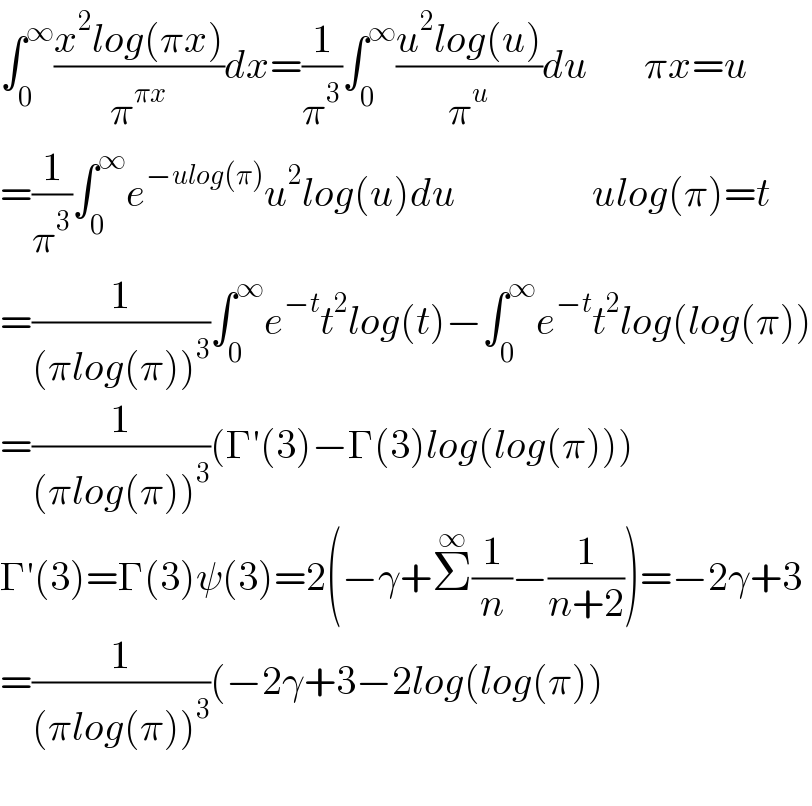
| ||
Question and Answers Forum | ||
Question Number 127017 by mnjuly1970 last updated on 26/Dec/20 | ||
![...NICE CALCULUS... prove that :: ∫_0 ^( ∞) (((x^2 ln(πx))/π^(πx) ))dx =(1/((πln(π))^3 ))[(3−2(γ+ln(ln(π)))]](Q127017.png) | ||
Answered by mindispower last updated on 26/Dec/20 | ||
![=∫_0 ^∞ x^2 ln(πx)e^(−πxln(π)) dx u=πln(π)x ⇒dx=(du/(πln(π))) ⇔∫_0 ^∞ (u^2 /(π^2 ln^2 (π)))ln((u/(ln(π))))e^(−u) .(du/(πln(π))) =(1/(π^3 ln^3 (π)))[∫_0 ^∞ u^2 ln(u)e^(−u) du−ln(lnπ)∫_0 ^∞ u^2 e^(−u) ] =(1/(π^3 ln^3 (π))){Γ′(3)−ln(ln(π).Γ(3)} =((Γ(3).Ψ(3))/(π^3 ln^3 (π)))−(1/(π^3 ln^3 (π)))2ln(lnπ) =2((1/2)+1−γ).(1/(π^3 ln^3 (π)))−((2ln(lnπ))/(π^3 ln^3 (π))) =((3−2γ)/(π^3 ln^3 (π)))−((2ln(lnπ))/(π^3 ln^3 (π)))=(1/((πlnπ)^3 ))[(3−2(γ+ln(lnπ))]](Q127019.png) | ||
| ||
Commented by mnjuly1970 last updated on 26/Dec/20 | ||
 | ||
Answered by Dwaipayan Shikari last updated on 26/Dec/20 | ||
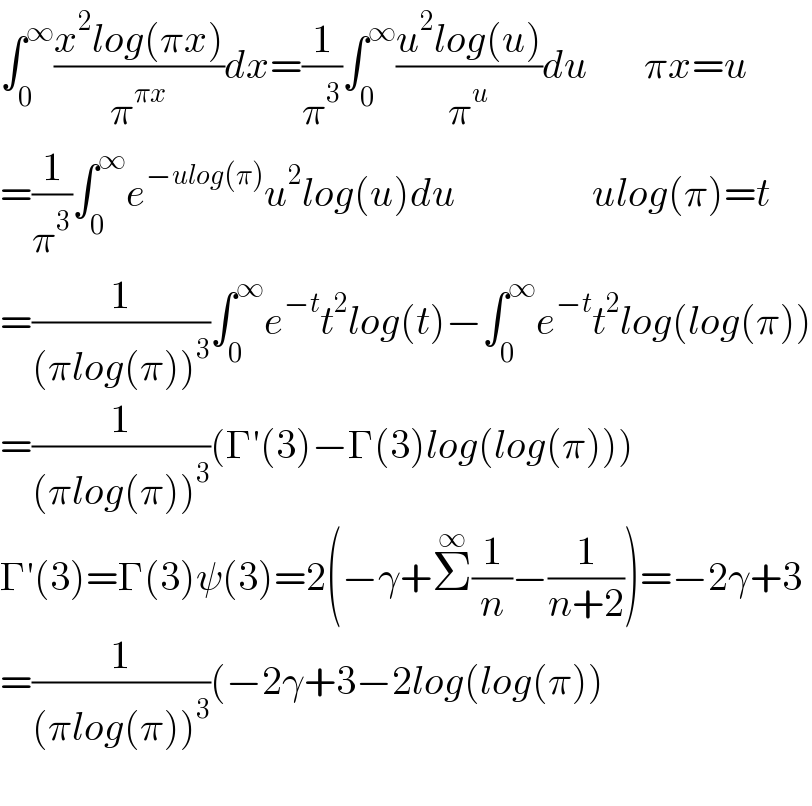 | ||
| ||