
Question Number 127094 by kolos last updated on 26/Dec/20

Commented by kolos last updated on 26/Dec/20
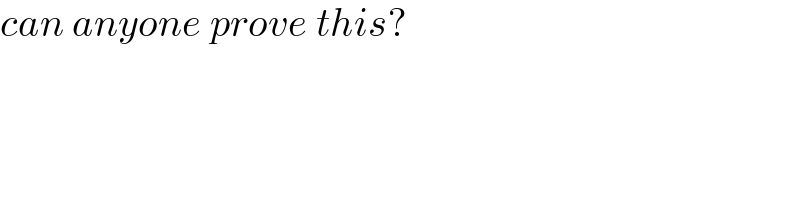
$${can}\:{anyone}\:{prove}\:{this}? \\ $$
Answered by mindispower last updated on 27/Dec/20
![x−(1/2)−(1/π)arctan(tg(πx−(π/2)))=f(x) f(1+x)=x+(1/2)−(1/π)arctan(tg(πx+π−(π/2))) =x+(1/2)−arctan(tg(πx−(π/2))=1+x−(1/2)−(1/π)arctan(tg(π(x−(1/2))) =1+f(x) suffisent to show ∀x∈[0,1[ [x]=x−(1/2)−((arctan(tg(π(x−(1/2)))))/π) arctan(tg(π(x−(1/2))).(1/π) x∈[0,1[]π(x−(1/2))∈[−(π/2),(π/2)] arctan(tg(π(x−(1/2)))=π(x−(1/2)) f(x)=x−(1/2)−(1/π)π(x−(1/2))=0=[x],∀x∈[0,1[ f(1+x)=1+f(x)=[1+x]=1+[x]⇒ by translation ∀x∈R [x]=x−(1/2)−((arctan(tg(π(x−(1/2))))/π)](Q127134.png)
$${x}−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\pi}{arctan}\left({tg}\left(\pi{x}−\frac{\pi}{\mathrm{2}}\right)\right)={f}\left({x}\right) \\ $$$${f}\left(\mathrm{1}+{x}\right)={x}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\pi}{arctan}\left({tg}\left(\pi{x}+\pi−\frac{\pi}{\mathrm{2}}\right)\right) \\ $$$$={x}+\frac{\mathrm{1}}{\mathrm{2}}−{arctan}\left({tg}\left(\pi{x}−\frac{\pi}{\mathrm{2}}\right)=\mathrm{1}+{x}−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\pi}{arctan}\left({tg}\left(\pi\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)\right)\right.\right. \\ $$$$=\mathrm{1}+{f}\left({x}\right) \\ $$$${suffisent}\:{to}\:{show}\:\forall{x}\in\left[\mathrm{0},\mathrm{1}\left[\right.\right. \\ $$$$\left[{x}\right]={x}−\frac{\mathrm{1}}{\mathrm{2}}−\frac{{arctan}\left({tg}\left(\pi\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)\right)\right)}{\pi}\: \\ $$$${arctan}\left({tg}\left(\pi\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)\right).\frac{\mathrm{1}}{\pi}\right. \\ $$$${x}\in\left[\mathrm{0},\mathrm{1}\left[\right]\pi\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)\in\left[−\frac{\pi}{\mathrm{2}},\frac{\pi}{\mathrm{2}}\right]\right. \\ $$$${arctan}\left({tg}\left(\pi\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)\right)=\pi\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)\right. \\ $$$${f}\left({x}\right)={x}−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\pi}\pi\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{0}=\left[{x}\right],\forall{x}\in\left[\mathrm{0},\mathrm{1}\left[\right.\right. \\ $$$${f}\left(\mathrm{1}+{x}\right)=\mathrm{1}+{f}\left({x}\right)=\left[\mathrm{1}+{x}\right]=\mathrm{1}+\left[{x}\right]\Rightarrow \\ $$$${by}\:{translation}\:\forall{x}\in\mathbb{R} \\ $$$$\left[{x}\right]={x}−\frac{\mathrm{1}}{\mathrm{2}}−\frac{{arctan}\left({tg}\left(\pi\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)\right)\right.}{\pi} \\ $$
