find the value of x such that { ((x=2 (mod 5))),((x=3 (mod 8) )),((x=2 (mod 3))) :}


Question and Answers Forum

All Questions Topic List
Number Theory Questions
Previous in All Question Next in All Question
Previous in Number Theory Next in Number Theory
Question Number 127111 by benjo_mathlover last updated on 26/Dec/20

$f i n d t h e v a l u e o f x s u c h t h a t$ ${\begin{cases} x = 2 (m o d 5) \\ x = 3 (m o d 8) \\ x = 2 (m o d 3) \end{cases}$
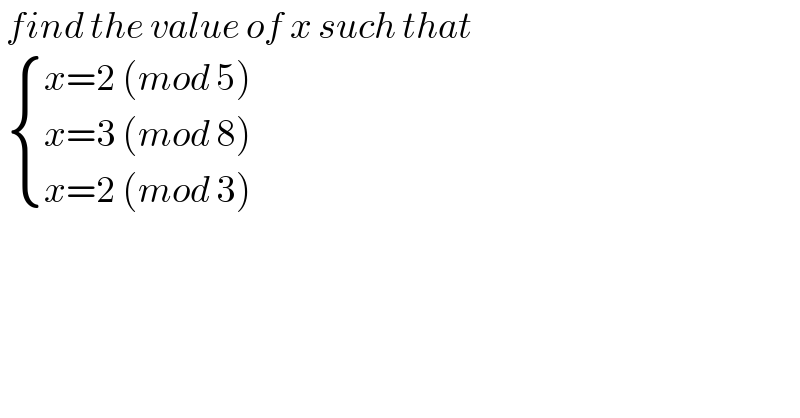
	Answered by liberty last updated on 04/Jan/21

	$g i v e n {\begin{cases} x = 2 (m o d 5) . . . (i) \\ x = 3 (m o d 8) . . . (i i) \\ x = 2 (m o d 3) . . . (i i i) \end{cases}$ $f o r (i) \Rightarrow 24 a \equiv 2 (m o d 5)$ $- a \equiv 2 (m o d 5); a \equiv - 2 (m o d 5)$ $f o r (i i) \Rightarrow 15 b \equiv 3 (m o d 8)$ $- b \equiv 3 (m o d 8); b \equiv - 3 (m o d 8)$ $f o r (i i i) \Rightarrow 40 c \equiv 2 (m o d 3)$ $c \equiv 2 (m o d 3)$ $n o w w e h a v e t h e g e n e r a l s o l u t i o n$ $∴ 24 (- 2) + 15 (- 3) + 40 (2) + 120 k; k \in Z$ $i . e : 120 k - 13; k \in Z or 120 k + 107; k \in Z$
	Answered by physicstutes last updated on 27/Dec/20

	$x \equiv 2 (\mod 3) . . . . . (i) \Rightarrow x = 3 t + 2, t \in Z . . . . . . (i)$ $x \equiv 3 (\mod 8) . . . . . . (i i)$ $(i) in (i) \Rightarrow 3 t + 2 \equiv 3 (\mod 8)$ $3 t \equiv - 1 (\mod 8)$ $but - 1 \equiv 7 (\mod 8) therefore$ $3 t \equiv 7 (\mod 8) by trial and error we find a number t which when$ $multiplied by 3 and divided by 8 gives a remainder of 7 .$ $so i find t = 3 after some tries .$ $\Rightarrow t \equiv 3 (\mod 8) \Rightarrow t = 8 s + 3, s \in Z . . . . . . (i i i)$ $putting (i i i) in (i) \Rightarrow x = 3 (8 s + 3) + 2 = 24 s + 11$ $so : x = 24 s + 11 . . . . . (i v)$ $x \equiv 2 (\mod 5) . . . . . . (v)$ $(i v) in (v) \Rightarrow 24 s + 11 \equiv 2 (\mod 5)$ $24 s \equiv - 9 (\mod 5)$ $but - 9 \equiv 1 (\mod 5) therefore 24 s \equiv 1 (\mod 5) by trial and error$ $s \equiv 4 (\mod 5) \Rightarrow s = 5 u + 4 . . . . . (v i i) u \in Z$ $\Rightarrow x = 24 (5 u + 4) + 11$ $x = 120 u + 107$ $x \equiv 107 (\mod 120)$
	Answered by floor(10²Eta[1]) last updated on 27/Dec/20

	$x \equiv 3 (\mod 8) \Rightarrow x = 8 a + 3, a \in Z$ $8 a + 3 \equiv 3 a + 3 \equiv 2 (\mod 5)$ $3 a \equiv 4 (\mod 5) \Rightarrow a \equiv 3 (\mod 5)$ $\Rightarrow a = 5 b + 3$ $\Rightarrow x = 8 (5 b + 3) + 3 = 40 b + 27, b \in Z$ $40 b + 27 \equiv b \equiv 2 (\mod 3) \Rightarrow b = 3 c + 2$ $\Rightarrow x = 40 (3 c + 2) + 27$ $\Rightarrow x = 120 c + 107, c \in Z$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum