Given a sequence (u_n ) defined reculsively by u_(n+1) = 3u_n + 4u_(n−1) , u_0 = 1 , u_2 = 3 show that u_(n+1) −4u_n = (−1)^(n+1) (3u_0 −4u_1 ) hence show that u


Question and Answers Forum

All Questions Topic List
Coordinate Geometry Questions
Previous in All Question Next in All Question
Previous in Coordinate Geometry Next in Coordinate Geometry
Question Number 127116 by physicstutes last updated on 27/Dec/20

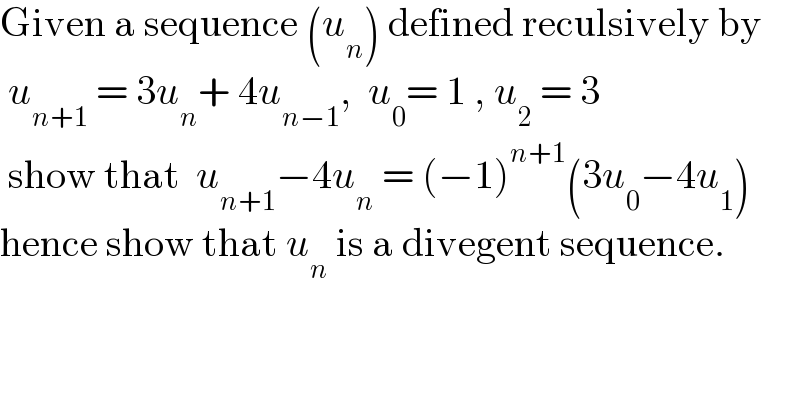
$Given a sequence (u_{n}) defined reculsively by$ $u_{n + 1} = 3 u_{n} + 4 u_{n - 1}, u_{0} = 1, u_{2} = 3$ $show that u_{n + 1} - 4 u_{n} = {(- 1)}^{n + 1} (3 u_{0} - 4 u_{1})$ $hence show that u_{n} is a divegent sequence .$
Commented by 676597498 last updated on 27/Dec/20

$f . m a t h s g c e 2020 .$ $i g o t t h e m a r k g u i d e$
Commented by Ar Brandon last updated on 27/Dec/20
Quel pays ?
	Answered by mr W last updated on 27/Dec/20

	$p^{2} - 3 p - 4 = 0$ $(p - 4) (p + 1) = 0$ $p = 4, - 1$ $u_{n} = A \times 4^{n} + B \times {(- 1)}^{n}$ $u_{2} = 16 A + B = 3$ $u_{0} = A + B = 1$ $\Rightarrow A = \frac{2}{15}$ $\Rightarrow B = \frac{13}{15}$ $u_{n} = \frac{2}{15} \times 4^{n} + \frac{13}{15} {(- 1)}^{n}$ $u_{1} = \frac{8}{15} - \frac{13}{15} = - \frac{1}{3}$ $3 u_{0} - 4 u_{1} = 3 + \frac{4}{3} = \frac{13}{3} = 5 B$ $u_{n + 1} - 4 u_{n} = A \times 4^{n + 1} + B \times {(- 1)}^{n + 1} - 4 A \times 4^{n} - 4 B \times {(- 1)}^{n}$ $= 5 B \times {(- 1)}^{n + 1} = {(- 1)}^{n + 1} (3 u_{0} - 4 u_{1})$
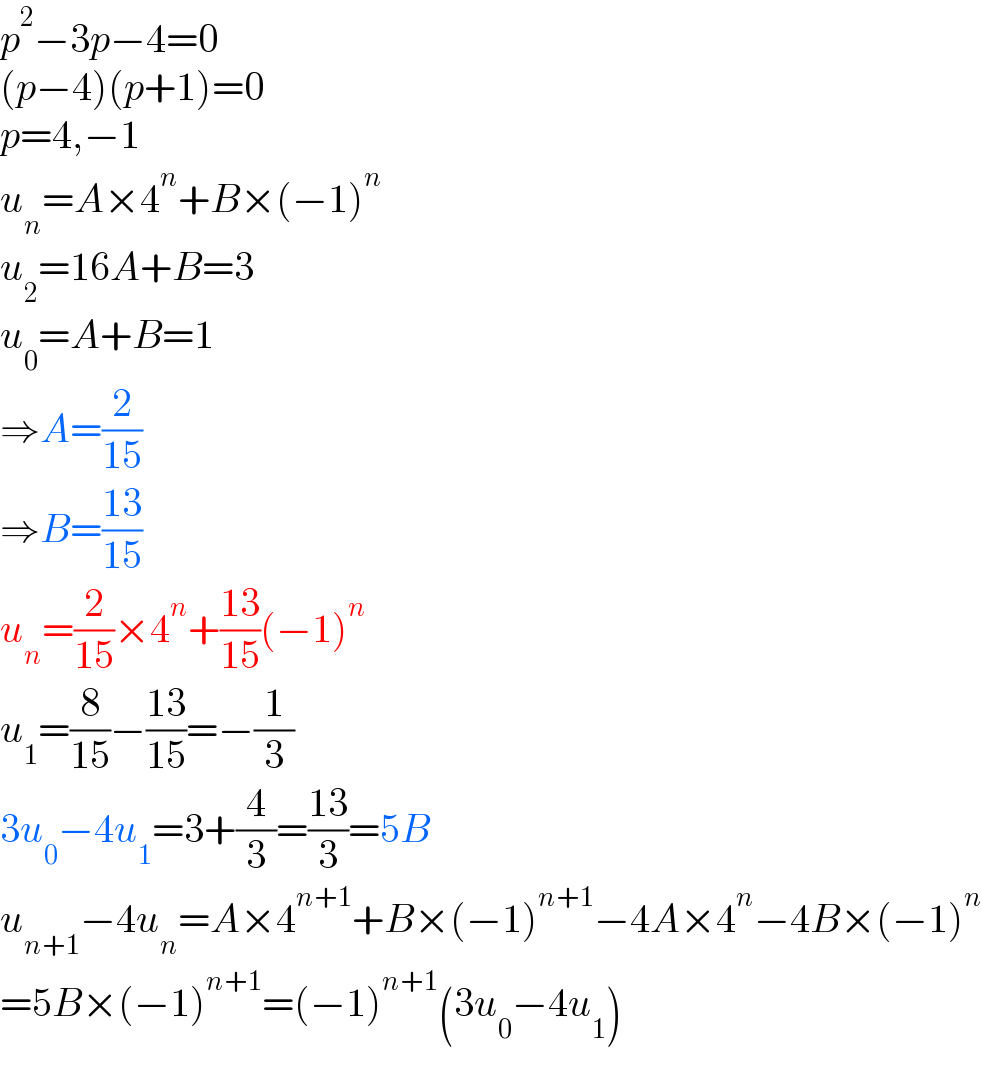
	Commented by physicstutes last updated on 27/Dec/20

	$thats wonderful gracias$
	Answered by Raxreedoroid last updated on 27/Dec/20

	$Given a sequence (u_{n}) defined reculsively by$ $u_{n + 1} = 3 u_{n} + 4 u_{n - 1}, u_{0} = 1, u_{2} = 3$ $show that u_{n + 1} - 4 u_{n} = {(- 1)}^{n + 1} (3 u_{0} - 4 u_{1})$ $hence show that u_{n} is a divegent sequence .$ $3 u_{1} = u_{2} - 4 u_{0}$ $u_{1} = \frac{3 - 4}{3} = - 0 . \overline{3}$ $u_{n + 1} - 4 u_{n} = {(- 1)}^{n + 1} (3 \times 1 + 4 \times 0 . \overline{3})$ $u_{n + 1} - 4 u_{n} = 4 . \bar{3} {(- 1)}^{n + 1}$ $L e t n = 1 t h e n u_{2} - 4 u_{1} = {(- 1)}^{1 + 1} (4 . \overline{3})$ $3 - 4 (- 0 . \bar{3}) = 4 . \bar{3}$ $4 . \bar{3} = 4 . \bar{3} ✓$ $(a) : A s s u m e u_{n + 1} - 4 u_{n} = 4 . \bar{3} {(- 1)}^{n + 1}$ $S u b t i t u t e x a s 4 . \bar{3} {(- 1)}^{n + 1} u_{n + 1} - 4 u_{n} = x$ $s o l v e f o r x$ $u_{n + 1} = 3 u_{n} + 4 u_{n - 1} ∴ 3 u_{n} + 4 u_{n - 1} - 4 u_{n} = x$ $x = 4 u_{n - 1} - u_{n}$ $∴ - x = u_{n} - 4 u_{n - 1}$ $u_{n} - 4 u_{n - 1} = 4 . \bar{3} (- 1) {(- 1)}^{n + 1}$ $u_{n} - 4 u_{n - 1} = 4 . \bar{3} {(- 1)}^{n + 2} = 4 . \bar{3} {(- 1)}^{2} {(- 1)}^{n} = 4 . \bar{3} {(- 1)}^{n}$ $S u b s i t u t e n a s n + 1$ $u_{n + 1} - 4 u_{n} = 4 . \bar{3} {(- 1)}^{n + 1} w h i c h i s t r u e f r o m (a)$ $u_{n + 1} = 4 . \bar{3} {(- 1)}^{n + 1} + 4 u_{n}$ $= 4 . \bar{3} {(- 1)}^{n + 1} + 4 \times 4 . \bar{3} {(- 1)}^{n} + 16 u_{n - 1} . . . 4^{n} {(- 1)}^{n + 1} + 4^{n + 1}$ $u_{n + 1} = 4^{n + 1} + \underset{i = 1}{\sum^{n + 1}} 4^{i - 1} \times 4 . \bar{3} {(- 1)}^{n - i}$ $u_{n} = 4^{n} + 4 . \bar{3} \underset{i = 1}{\sum^{n}} 4^{i - 1} {(- 1)}^{n - i - 1}$ $u_{n} = 4^{n} + 4 . \bar{3} \underset{i = 1}{\sum^{n}} 4^{i - 1} {(- 1)}^{n - i - 1}$ $\underset{n \to \infty}{l i m} (4^{n} + 4 . \bar{3} \underset{i = 1}{\sum^{n}} 4^{i - 1} {(- 1)}^{n - i - 1}) = \infty$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum