Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 127152 by mnjuly1970 last updated on 27/Dec/20

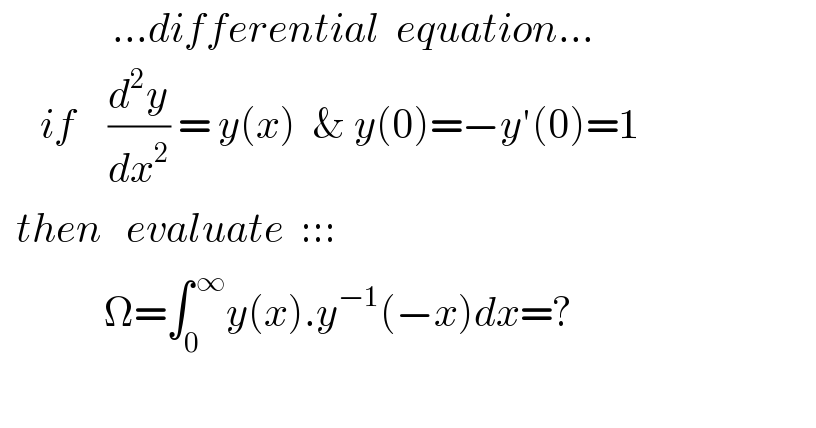
...differential equation... if (d^2 y/dx^2 ) = y(x) & y(0)=−y′(0)=1 then evaluate ::: Ω=∫_0 ^( ∞) y(x).y^(−1) (−x)dx=?

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:...{differential}\:\:{equation}...\:\:\:\:\:\:\:\: \\ $$ $$\:\:\:\:\:{if}\:\:\:\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:=\:{y}\left({x}\right)\:\:\&\:{y}\left(\mathrm{0}\right)=−{y}'\left(\mathrm{0}\right)=\mathrm{1} \\ $$ $$\:\:{then}\:\:\:{evaluate}\:\:::: \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\Omega=\int_{\mathrm{0}} ^{\:\infty} {y}\left({x}\right).{y}^{−\mathrm{1}} \left(−{x}\right){dx}=? \\ $$ $$ \\ $$

Answered by mathmax by abdo last updated on 27/Dec/20

y^(′′) =y and y(0)=1 ,y^′ (0)=−1 r^2 −1=0 ⇒y =ae^x +be^(−x) y(0)=1 ⇒a+b=1 ,y^′ =ae^x −be^(−x) ,y^′ (0)=−1 ⇒a−b=−1 ⇒ { ((a+b=1)),((a−b=−1 ⇒ { ((a=0 ⇒y(x)=e^(−x) )),((b=1 )) :})) :} y(x)=t ⇒x=y^(−1) (t) ⇒e^(−x) =t ⇒−x =ln(t) ⇒x=−lnt ⇒ y^(−1) (x)=−lnx ⇒Ω =∫_0 ^∞ e^(−x) (−ln(−x))dx =−∫_0 ^∞ e^(−x) (iπ +ln(x))dx =−iπ ∫_0 ^∞ e^(−x) dx −∫_0 ^∞ e^(−x) ln(x)dx =−iπ[−e^(−x) ]_0 ^∞ +γ =γ−iπ

$$\mathrm{y}^{''} =\mathrm{y}\:\:\mathrm{and}\:\mathrm{y}\left(\mathrm{0}\right)=\mathrm{1}\:,\mathrm{y}^{'} \left(\mathrm{0}\right)=−\mathrm{1} \\ $$ $$\mathrm{r}^{\mathrm{2}} −\mathrm{1}=\mathrm{0}\:\Rightarrow\mathrm{y}\:=\mathrm{ae}^{\mathrm{x}} \:+\mathrm{be}^{−\mathrm{x}} \\ $$ $$\mathrm{y}\left(\mathrm{0}\right)=\mathrm{1}\:\Rightarrow\mathrm{a}+\mathrm{b}=\mathrm{1}\:,\mathrm{y}^{'} \:=\mathrm{ae}^{\mathrm{x}} −\mathrm{be}^{−\mathrm{x}} \:,\mathrm{y}^{'} \left(\mathrm{0}\right)=−\mathrm{1}\:\Rightarrow\mathrm{a}−\mathrm{b}=−\mathrm{1}\:\Rightarrow \\ $$ $$\begin{cases}{\mathrm{a}+\mathrm{b}=\mathrm{1}}\\{\mathrm{a}−\mathrm{b}=−\mathrm{1}\:\:\Rightarrow\begin{cases}{\mathrm{a}=\mathrm{0}\:\Rightarrow\mathrm{y}\left(\mathrm{x}\right)=\mathrm{e}^{−\mathrm{x}} }\\{\mathrm{b}=\mathrm{1}\:\:}\end{cases}}\end{cases} \\ $$ $$\mathrm{y}\left(\mathrm{x}\right)=\mathrm{t}\:\Rightarrow\mathrm{x}=\mathrm{y}^{−\mathrm{1}} \left(\mathrm{t}\right)\:\Rightarrow\mathrm{e}^{−\mathrm{x}} \:=\mathrm{t}\:\Rightarrow−\mathrm{x}\:=\mathrm{ln}\left(\mathrm{t}\right)\:\Rightarrow\mathrm{x}=−\mathrm{lnt}\:\Rightarrow \\ $$ $$\mathrm{y}^{−\mathrm{1}} \left(\mathrm{x}\right)=−\mathrm{lnx}\:\Rightarrow\Omega\:=\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{e}^{−\mathrm{x}} \:\left(−\mathrm{ln}\left(−\mathrm{x}\right)\right)\mathrm{dx} \\ $$ $$=−\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{x}} \left(\mathrm{i}\pi\:+\mathrm{ln}\left(\mathrm{x}\right)\right)\mathrm{dx}\:\:=−\mathrm{i}\pi\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{x}} \mathrm{dx}\:−\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{x}\right)\mathrm{dx} \\ $$ $$=−\mathrm{i}\pi\left[−\mathrm{e}^{−\mathrm{x}} \right]_{\mathrm{0}} ^{\infty} +\gamma\:\:=\gamma−\mathrm{i}\pi \\ $$

Commented bymnjuly1970 last updated on 27/Dec/20

thanks alot sir max...

$${thanks}\:{alot}\:{sir}\:\:{max}... \\ $$

Commented bymathmax by abdo last updated on 27/Dec/20

you are welcome

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$

Answered by mnjuly1970 last updated on 27/Dec/20

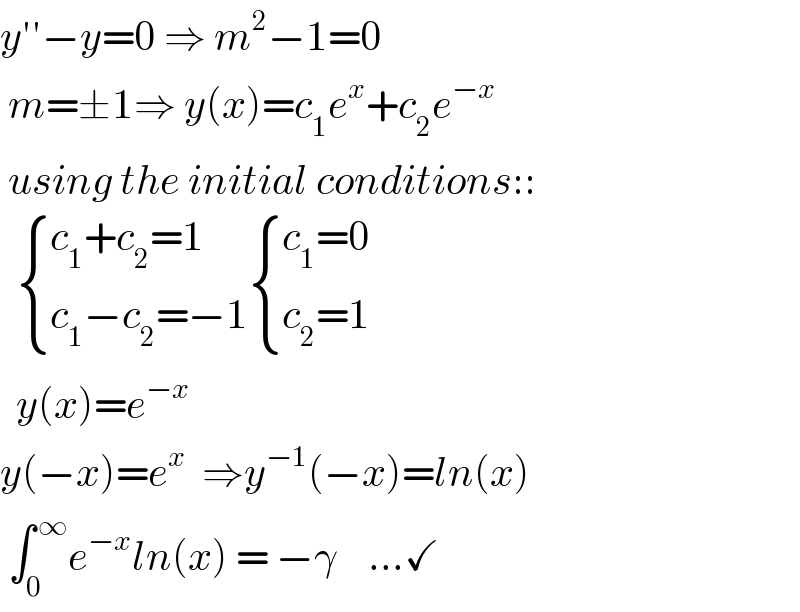
y′′−y=0 ⇒ m^2 −1=0 m=±1⇒ y(x)=c_1 e^x +c_2 e^(−x) using the initial conditions:: { ((c_1 +c_2 =1)),((c_1 −c_2 =−1)) :} { ((c_1 =0)),((c_2 =1)) :} y(x)=e^(−x) y(−x)=e^x ⇒y^(−1) (−x)=ln(x) ∫_(0 ) ^( ∞) e^(−x) ln(x) = −γ ...✓

$${y}''−{y}=\mathrm{0}\:\Rightarrow\:{m}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$ $$\:{m}=\pm\mathrm{1}\Rightarrow\:{y}\left({x}\right)={c}_{\mathrm{1}} {e}^{{x}} +{c}_{\mathrm{2}} {e}^{−{x}} \\ $$ $$\:{using}\:{the}\:{initial}\:{conditions}:: \\ $$ $$\:\:\begin{cases}{{c}_{\mathrm{1}} +{c}_{\mathrm{2}} =\mathrm{1}}\\{{c}_{\mathrm{1}} −{c}_{\mathrm{2}} =−\mathrm{1}}\end{cases}\begin{cases}{{c}_{\mathrm{1}} =\mathrm{0}}\\{{c}_{\mathrm{2}} =\mathrm{1}}\end{cases} \\ $$ $$\:\:{y}\left({x}\right)={e}^{−{x}} \\ $$ $${y}\left(−{x}\right)={e}^{{x}} \:\:\Rightarrow{y}^{−\mathrm{1}} \left(−{x}\right)={ln}\left({x}\right) \\ $$ $$\:\int_{\mathrm{0}\:} ^{\:\infty} {e}^{−{x}} {ln}\left({x}\right)\:=\:−\gamma\:\:\:\:...\checkmark \\ $$

Answered by Dwaipayan Shikari last updated on 27/Dec/20

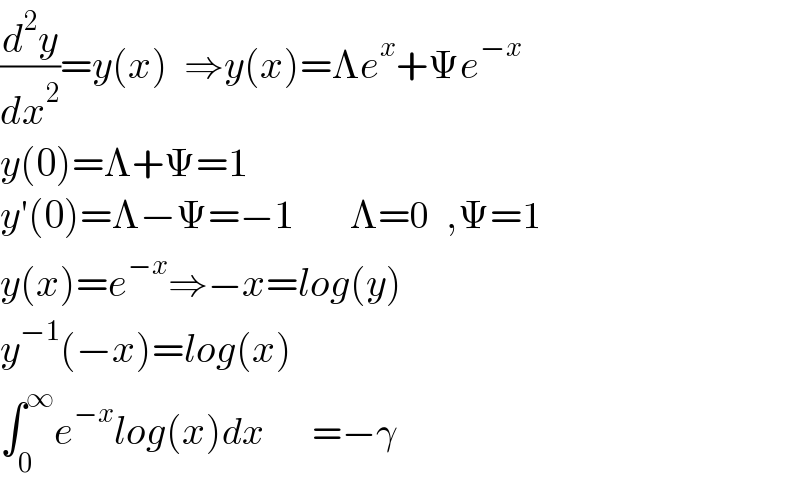
(d^2 y/dx^2 )=y(x) ⇒y(x)=Λe^x +Ψe^(−x) y(0)=Λ+Ψ=1 y′(0)=Λ−Ψ=−1 Λ=0 ,Ψ=1 y(x)=e^(−x) ⇒−x=log(y) y^(−1) (−x)=log(x) ∫_0 ^∞ e^(−x) log(x)dx =−γ

$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }={y}\left({x}\right)\:\:\Rightarrow{y}\left({x}\right)=\Lambda{e}^{{x}} +\Psi{e}^{−{x}} \\ $$ $${y}\left(\mathrm{0}\right)=\Lambda+\Psi=\mathrm{1} \\ $$ $${y}'\left(\mathrm{0}\right)=\Lambda−\Psi=−\mathrm{1}\:\:\:\:\:\:\:\Lambda=\mathrm{0}\:\:,\Psi=\mathrm{1} \\ $$ $${y}\left({x}\right)={e}^{−{x}} \Rightarrow−{x}={log}\left({y}\right) \\ $$ $${y}^{−\mathrm{1}} \left(−{x}\right)={log}\left({x}\right) \\ $$ $$\int_{\mathrm{0}} ^{\infty} {e}^{−{x}} {log}\left({x}\right){dx}\:\:\:\:\:\:=−\gamma \\ $$

Commented bymnjuly1970 last updated on 27/Dec/20

grateful...

$${grateful}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com