
Question and Answers Forum
Question Number 127160 by kaivan.ahmadi last updated on 27/Dec/20
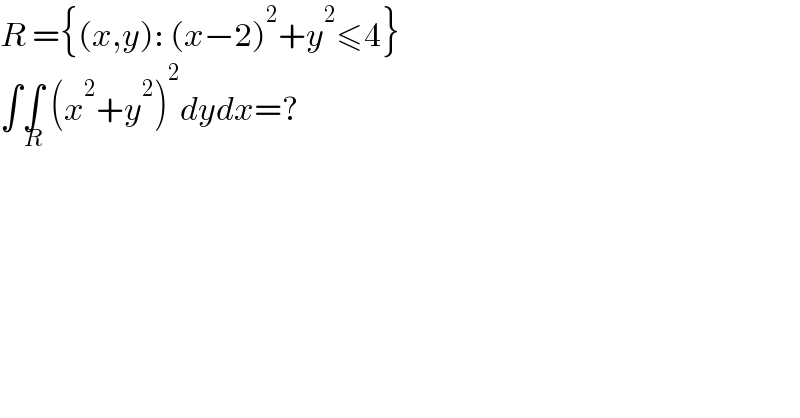
Answered by mathmax by abdo last updated on 27/Dec/20
![we use the diffeomorphism { ((x−2=rcosθ)),((y=rsinθ)) :} (x−2)^2 +y^2 ≤4 ⇒r^2 ≤4 ⇒0≤r≤2 ∫∫_R (x^2 +y^2 )^2 dxdy =∫_0 ^2 ∫_(−π) ^π ((rcosθ +2)^2 +r^2 sin^2 θ)^2 rdrdθ = ∫_0 ^2 ∫_(−π) ^π {r^2 cos^2 θ +4rcosθ +4+r^2 sin^2 θ)^2 drdθ = ∫_0 ^2 ∫_(−π) ^π {r^2 +4rcosθ +4)^2 drdθ =∫_0 ^2 ∫_(−π) ^π {(r^2 +4)^2 +8rcosθ(r^2 +4)+16r^2 cos^2 θ}drdθ =2π ∫_0 ^2 (r^2 +4)^(2 ) dr +8 ∫_0 ^2 (r^3 +4r)dr∫_(−π) ^π cosθ dθ(→0)+16∫_0 ^2 r^2 dr∫_(−π) ^π cos^2 θ dθ ∫_0 ^2 (r^2 +4)^2 dr =∫_0 ^2 (r^4 +8r^2 +16)dr =[(r^5 /5)+(8/3)r^3 +16r]_0 ^2 =.... ∫_0 ^2 r^2 dr =[(r^3 /3)]_0 ^2 =(8/3) ∫_(−π) ^π cos^2 θ dθ =2∫_0 ^π ((1+cos(2θ))/2)dθ =π rest to collect the values...](Q127183.png)
| ||
Question and Answers Forum | ||
Question Number 127160 by kaivan.ahmadi last updated on 27/Dec/20 | ||
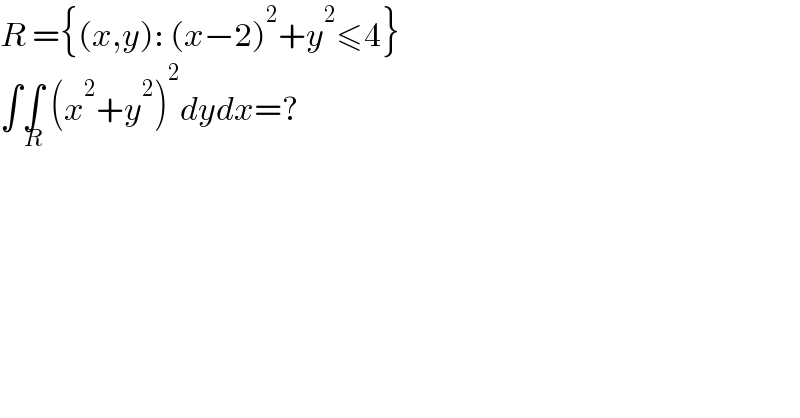 | ||
Answered by mathmax by abdo last updated on 27/Dec/20 | ||
![we use the diffeomorphism { ((x−2=rcosθ)),((y=rsinθ)) :} (x−2)^2 +y^2 ≤4 ⇒r^2 ≤4 ⇒0≤r≤2 ∫∫_R (x^2 +y^2 )^2 dxdy =∫_0 ^2 ∫_(−π) ^π ((rcosθ +2)^2 +r^2 sin^2 θ)^2 rdrdθ = ∫_0 ^2 ∫_(−π) ^π {r^2 cos^2 θ +4rcosθ +4+r^2 sin^2 θ)^2 drdθ = ∫_0 ^2 ∫_(−π) ^π {r^2 +4rcosθ +4)^2 drdθ =∫_0 ^2 ∫_(−π) ^π {(r^2 +4)^2 +8rcosθ(r^2 +4)+16r^2 cos^2 θ}drdθ =2π ∫_0 ^2 (r^2 +4)^(2 ) dr +8 ∫_0 ^2 (r^3 +4r)dr∫_(−π) ^π cosθ dθ(→0)+16∫_0 ^2 r^2 dr∫_(−π) ^π cos^2 θ dθ ∫_0 ^2 (r^2 +4)^2 dr =∫_0 ^2 (r^4 +8r^2 +16)dr =[(r^5 /5)+(8/3)r^3 +16r]_0 ^2 =.... ∫_0 ^2 r^2 dr =[(r^3 /3)]_0 ^2 =(8/3) ∫_(−π) ^π cos^2 θ dθ =2∫_0 ^π ((1+cos(2θ))/2)dθ =π rest to collect the values...](Q127183.png) | ||
| ||