
Question Number 127182 by danielasebhofoh last updated on 27/Dec/20

Answered by Dwaipayan Shikari last updated on 27/Dec/20
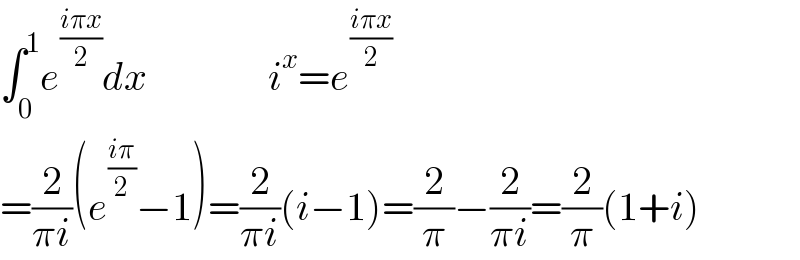
$$\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{\frac{{i}\pi{x}}{\mathrm{2}}} {dx}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{i}^{{x}} ={e}^{\frac{{i}\pi{x}}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{2}}{\pi{i}}\left({e}^{\frac{{i}\pi}{\mathrm{2}}} −\mathrm{1}\right)=\frac{\mathrm{2}}{\pi{i}}\left({i}−\mathrm{1}\right)=\frac{\mathrm{2}}{\pi}−\frac{\mathrm{2}}{\pi{i}}=\frac{\mathrm{2}}{\pi}\left(\mathrm{1}+{i}\right) \\ $$
Answered by Ar Brandon last updated on 27/Dec/20
![I=∫_0 ^1 i^x dx=[(i^x /(lni))]_0 ^1 =(i/(lni))−(1/(lni)) , i=e^((π/2)i) =(i/((π/2)i))−(1/((π/2)i))=(2/π)−(2/(iπ))](Q127185.png)
$$\mathcal{I}=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{i}^{\mathrm{x}} \mathrm{dx}=\left[\frac{\mathrm{i}^{\mathrm{x}} }{\mathrm{lni}}\right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{i}}{\mathrm{lni}}−\frac{\mathrm{1}}{\mathrm{lni}}\:,\:\mathrm{i}=\mathrm{e}^{\frac{\pi}{\mathrm{2}}\mathrm{i}} \\ $$$$\:\:\:=\frac{\mathrm{i}}{\left(\pi/\mathrm{2}\right)\mathrm{i}}−\frac{\mathrm{1}}{\left(\pi/\mathrm{2}\right)\mathrm{i}}=\frac{\mathrm{2}}{\pi}−\frac{\mathrm{2}}{\mathrm{i}\pi} \\ $$
