∫_0 ^( π^2 ) x^(−(1/2)) e^(−x) dx


Question and Answers Forum

All Questions Topic List
None Questions
Previous in All Question Next in All Question
Previous in None Next in None
Question Number 127211 by mohammad17 last updated on 27/Dec/20

$\int_{0}^{π^{2}} x^{- \frac{1}{2}} e^{- x} d x$
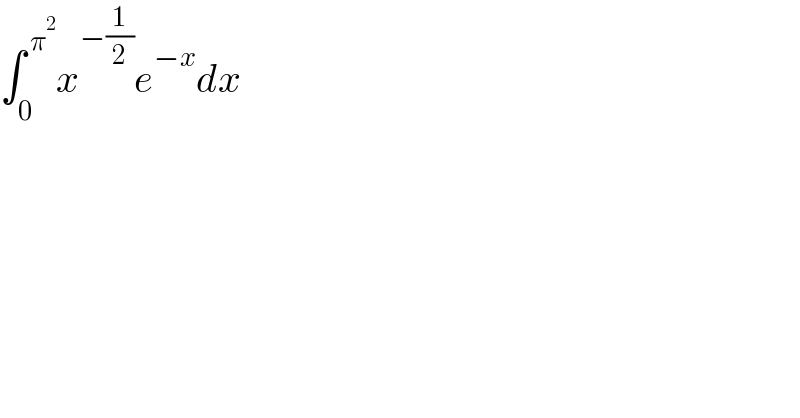
	Answered by Dwaipayan Shikari last updated on 27/Dec/20

	$\int_{0}^{π^{2}} x^{- \frac{1}{2}} e^{- x} d x x = u^{2} \Rightarrow 1 = 2 u \frac{d u}{d x}$ $= 2 \int_{0}^{π} e^{- u^{2}} d u = 2 \int_{0}^{\infty} e^{- u^{2}} d u - 2 \int_{π}^{\infty} e^{- u^{2}} d u$ $= \sqrt{π} - \frac{2 e^{- π^{2}}}{2 π + \frac{1}{π + \frac{2}{2 π + \frac{3}{π + . . .}}}}$ $O r \int_{0}^{π^{2}} x^{- \frac{1}{2}} e^{- x} d x = \int_{0}^{\infty} x^{- \frac{1}{2}} e^{- x} - \int_{π^{2}}^{\infty} x^{- \frac{1}{2}} e^{- x^{2}} = Γ (\frac{1}{2}) - Γ (\frac{1}{2}, π^{2})$ $I n c o m p l e t e G a m m a Γ (a, z) = \int_{z}^{\infty} t^{a - 1} e^{- t} d t$
	Commented by mohammad17 last updated on 27/Dec/20

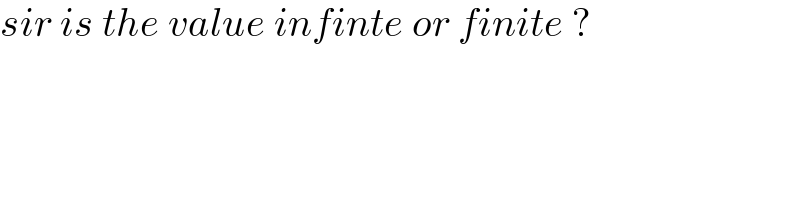
	$s i r i s t h e v a l u e i n f i n t e o r f i n i t e ?$
	Commented by Dwaipayan Shikari last updated on 27/Dec/20
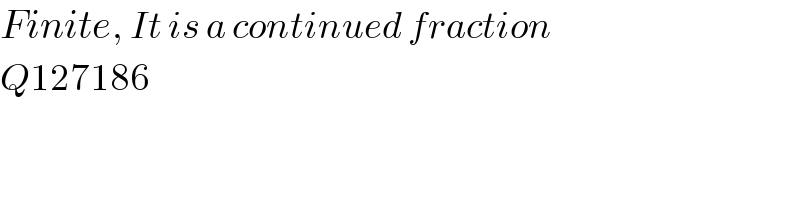
	$Finite, It is a continued fraction Q127186$
	$F i n i t e, I t i s a c o n t i n u e d f r a c t i o n$ $Q 127186$
	Answered by mindispower last updated on 28/Dec/20

	$\sum_{k ⩾ 0} \int^{π^{2}} x^{- \frac{1}{2}} . \frac{{(- x)}^{k}}{k!} d x$ $= \sum_{k ⩾ 0} \frac{{(- 1)}^{k}}{k!} \int_{0}^{π^{2}} x^{k - \frac{1}{2}} d x$ $= \sum_{k ⩾ 0} \frac{{(- 1)}^{k}}{k!} {[\frac{x^{k + \frac{1}{2}}}{k + \frac{1}{2}}]}_{0}^{π} = \sum_{k ⩾ 0} \frac{{(- 1)}^{k} π^{2 k + 1}}{(k + \frac{1}{2}) k!}$ $= 2 π + 2 π \sum_{k ⩾ 1} \frac{\underset{j = 0}{\prod^{k - 1}} (\frac{1}{2} + j)}{\underset{j = 0}{\prod^{k - 1}} (\frac{3}{2} + j)} . \frac{{(- π^{2})}^{k}}{k!}$ $= 2 π (1 + \sum_{k ⩾ 1} \frac{{(\frac{1}{2})}_{k}}{{(\frac{3}{2})}_{k}} . \frac{{(- π^{2})}^{k}}{k!})$ $= 2 π_{1} F_{1} (\frac{1}{2}; \frac{3}{2}; - π^{2})$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum