Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 127260 by bramlexs22 last updated on 28/Dec/20

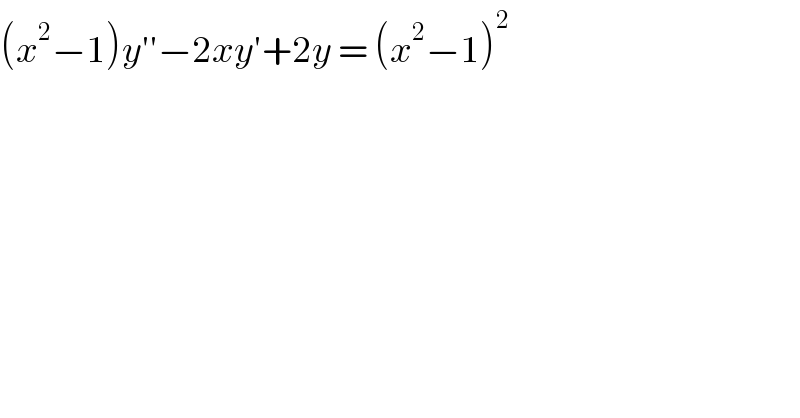
(x^2 −1)y′′−2xy′+2y = (x^2 −1)^2

$$\left({x}^{\mathrm{2}} −\mathrm{1}\right){y}''−\mathrm{2}{xy}'+\mathrm{2}{y}\:=\:\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \\ $$

Answered by liberty last updated on 28/Dec/20

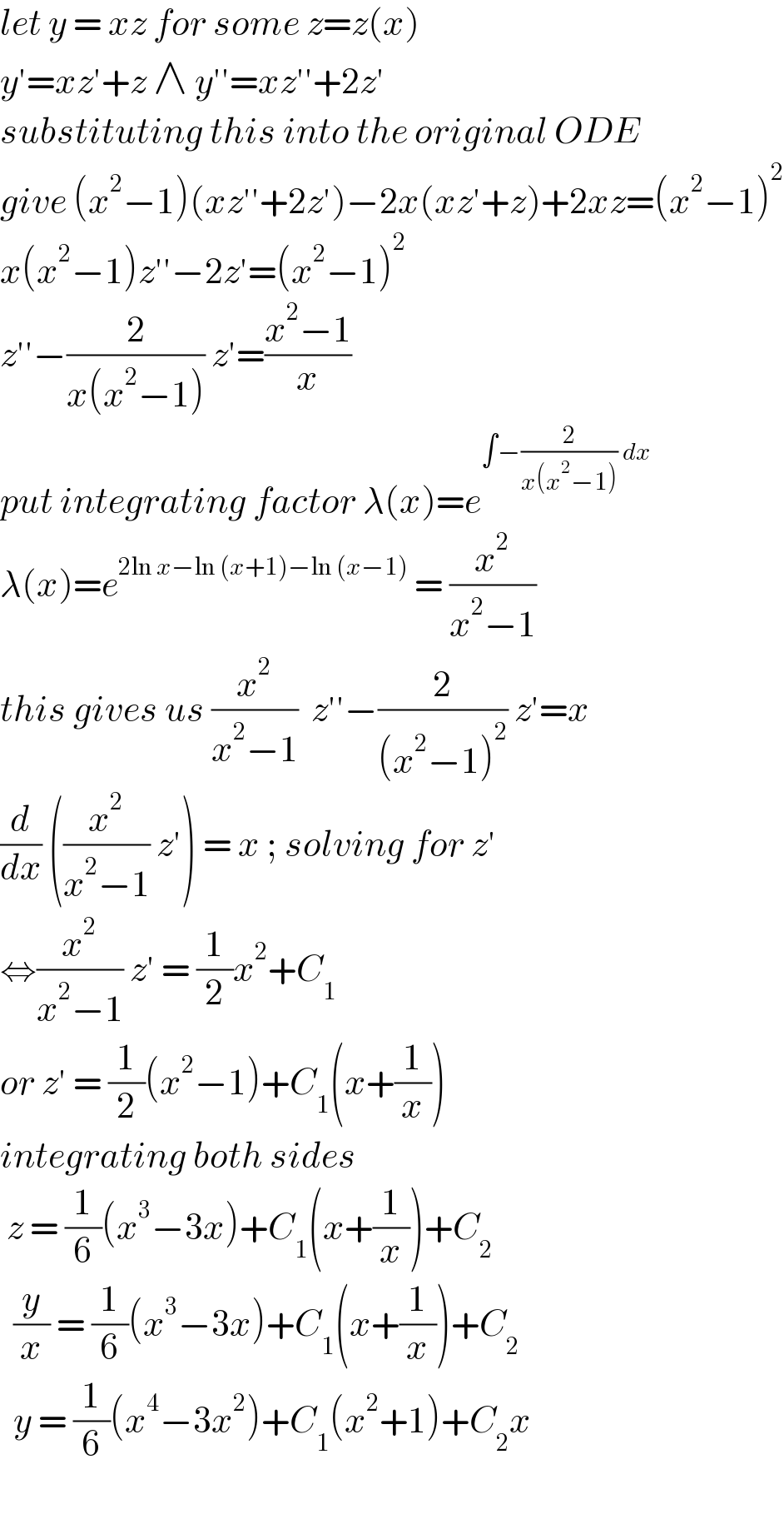
let y = xz for some z=z(x) y′=xz′+z ∧ y′′=xz′′+2z′ substituting this into the original ODE give (x^2 −1)(xz′′+2z′)−2x(xz′+z)+2xz=(x^2 −1)^2 x(x^2 −1)z′′−2z′=(x^2 −1)^2 z′′−(2/(x(x^2 −1))) z′=((x^2 −1)/x) put integrating factor λ(x)=e^(∫−(2/(x(x^2 −1))) dx) λ(x)=e^(2ln x−ln (x+1)−ln (x−1)) = (x^2 /(x^2 −1)) this gives us (x^2 /(x^2 −1)) z′′−(2/((x^2 −1)^2 )) z′=x (d/dx) ((x^2 /(x^2 −1)) z′) = x ; solving for z′ ⇔(x^2 /(x^2 −1)) z′ = (1/2)x^2 +C_1 or z′ = (1/2)(x^2 −1)+C_1 (x+(1/x)) integrating both sides z = (1/6)(x^3 −3x)+C_1 (x+(1/x))+C_2 (y/x) = (1/6)(x^3 −3x)+C_1 (x+(1/x))+C_2 y = (1/6)(x^4 −3x^2 )+C_1 (x^2 +1)+C_2 x

$${let}\:{y}\:=\:{xz}\:{for}\:{some}\:{z}={z}\left({x}\right) \\ $$$${y}'={xz}'+{z}\:\wedge\:{y}''={xz}''+\mathrm{2}{z}' \\ $$$${substituting}\:{this}\:{into}\:{the}\:{original}\:{ODE} \\ $$$${give}\:\left({x}^{\mathrm{2}} −\mathrm{1}\right)\left({xz}''+\mathrm{2}{z}'\right)−\mathrm{2}{x}\left({xz}'+{z}\right)+\mathrm{2}{xz}=\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \\ $$$${x}\left({x}^{\mathrm{2}} −\mathrm{1}\right){z}''−\mathrm{2}{z}'=\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \\ $$$${z}''−\frac{\mathrm{2}}{{x}\left({x}^{\mathrm{2}} −\mathrm{1}\right)}\:{z}'=\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}} \\ $$$${put}\:{integrating}\:{factor}\:\lambda\left({x}\right)={e}^{\int−\frac{\mathrm{2}}{{x}\left({x}^{\mathrm{2}} −\mathrm{1}\right)}\:{dx}} \\ $$$$\lambda\left({x}\right)={e}^{\mathrm{2ln}\:{x}−\mathrm{ln}\:\left({x}+\mathrm{1}\right)−\mathrm{ln}\:\left({x}−\mathrm{1}\right)} \:=\:\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} −\mathrm{1}} \\ $$$${this}\:{gives}\:{us}\:\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} −\mathrm{1}}\:\:{z}''−\frac{\mathrm{2}}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }\:{z}'={x} \\ $$$$\frac{{d}}{{dx}}\:\left(\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} −\mathrm{1}}\:{z}'\right)\:=\:{x}\:;\:{solving}\:{for}\:{z}' \\ $$$$\Leftrightarrow\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} −\mathrm{1}}\:{z}'\:=\:\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} +{C}_{\mathrm{1}} \\ $$$${or}\:{z}'\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left({x}^{\mathrm{2}} −\mathrm{1}\right)+{C}_{\mathrm{1}} \left({x}+\frac{\mathrm{1}}{{x}}\right) \\ $$$${integrating}\:{both}\:{sides}\: \\ $$$$\:{z}\:=\:\frac{\mathrm{1}}{\mathrm{6}}\left({x}^{\mathrm{3}} −\mathrm{3}{x}\right)+{C}_{\mathrm{1}} \left({x}+\frac{\mathrm{1}}{{x}}\right)+{C}_{\mathrm{2}} \\ $$$$\:\:\frac{{y}}{{x}}\:=\:\frac{\mathrm{1}}{\mathrm{6}}\left({x}^{\mathrm{3}} −\mathrm{3}{x}\right)+{C}_{\mathrm{1}} \left({x}+\frac{\mathrm{1}}{{x}}\right)+{C}_{\mathrm{2}} \\ $$$$\:\:{y}\:=\:\frac{\mathrm{1}}{\mathrm{6}}\left({x}^{\mathrm{4}} −\mathrm{3}{x}^{\mathrm{2}} \right)+{C}_{\mathrm{1}} \left({x}^{\mathrm{2}} +\mathrm{1}\right)+{C}_{\mathrm{2}} {x}\: \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com