Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 127315 by mnjuly1970 last updated on 28/Dec/20

...advanced calculud... compute ::: ψ(i)=??

$$\:\:\:\:\:\:\:\:\:...{advanced}\:\:\:{calculud}... \\ $$$$\:\:\:\:{compute}\:\:::: \\ $$$$\:\:\:\:\:\psi\left({i}\right)=?? \\ $$$$\:\:\:\:\:\:\: \\ $$

Commented by Dwaipayan Shikari last updated on 28/Dec/20

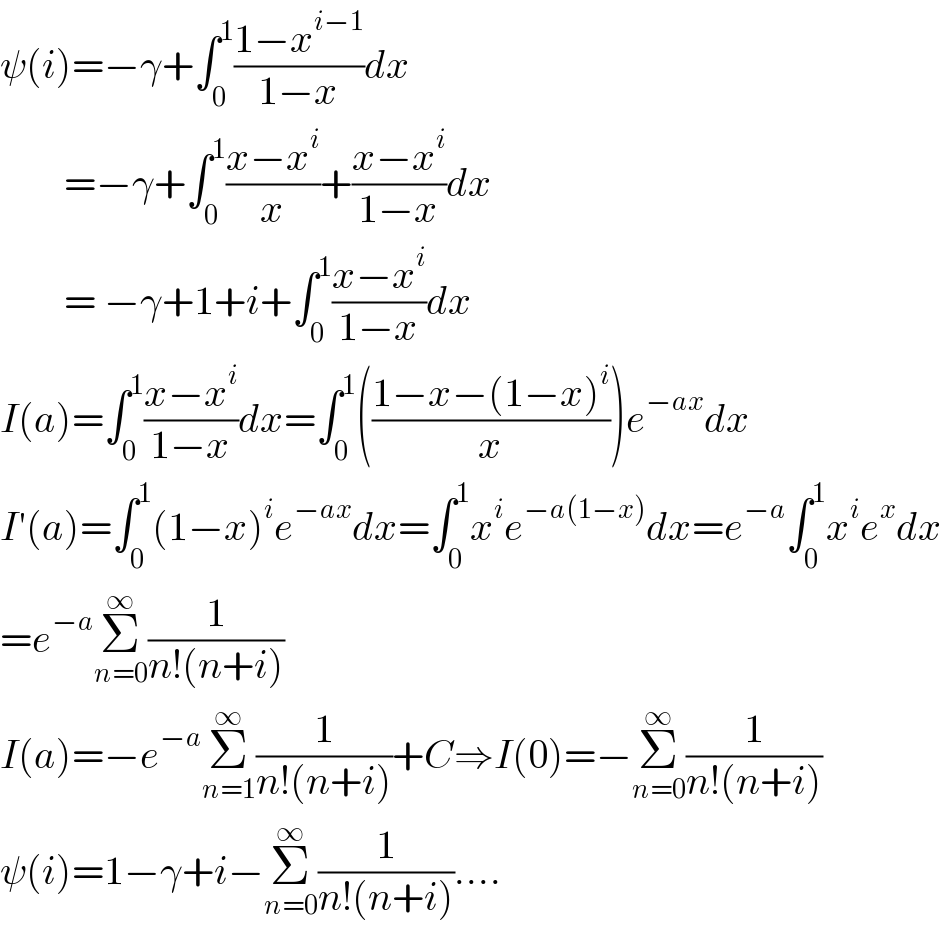
ψ(i)=−γ+∫_0 ^1 ((1−x^(i−1) )/(1−x))dx =−γ+∫_0 ^1 ((x−x^i )/x)+((x−x^i )/(1−x))dx = −γ+1+i+∫_0 ^1 ((x−x^i )/(1−x))dx I(a)=∫_0 ^1 ((x−x^i )/(1−x))dx=∫_0 ^1 (((1−x−(1−x)^i )/x))e^(−ax) dx I′(a)=∫_0 ^1 (1−x)^i e^(−ax) dx=∫_0 ^1 x^i e^(−a(1−x)) dx=e^(−a) ∫_0 ^1 x^i e^x dx =e^(−a) Σ_(n=0) ^∞ (1/(n!(n+i))) I(a)=−e^(−a) Σ_(n=1) ^∞ (1/(n!(n+i)))+C⇒I(0)=−Σ_(n=0) ^∞ (1/(n!(n+i))) ψ(i)=1−γ+i−Σ_(n=0) ^∞ (1/(n!(n+i)))....

$$\psi\left({i}\right)=−\gamma+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{x}^{{i}−\mathrm{1}} }{\mathrm{1}−{x}}{dx} \\ $$$$\:\:\:\:\:\:\:\:=−\gamma+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}−{x}^{{i}} }{{x}}+\frac{{x}−{x}^{{i}} }{\mathrm{1}−{x}}{dx} \\ $$$$\:\:\:\:\:\:\:\:=\:−\gamma+\mathrm{1}+{i}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}−{x}^{{i}} }{\mathrm{1}−{x}}{dx} \\ $$$${I}\left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}−{x}^{{i}} }{\mathrm{1}−{x}}{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{1}−{x}−\left(\mathrm{1}−{x}\right)^{{i}} }{{x}}\right){e}^{−{ax}} {dx} \\ $$$${I}'\left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}\right)^{{i}} {e}^{−{ax}} {dx}=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{i}} {e}^{−{a}\left(\mathrm{1}−{x}\right)} {dx}={e}^{−{a}} \int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{i}} {e}^{{x}} {dx} \\ $$$$={e}^{−{a}} \underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!\left({n}+{i}\right)} \\ $$$${I}\left({a}\right)=−{e}^{−{a}} \underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!\left({n}+{i}\right)}+{C}\Rightarrow{I}\left(\mathrm{0}\right)=−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!\left({n}+{i}\right)} \\ $$$$\psi\left({i}\right)=\mathrm{1}−\gamma+{i}−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!\left({n}+{i}\right)}.... \\ $$

Commented by dsardor2004 last updated on 28/Dec/20

?

$$? \\ $$

Answered by Olaf last updated on 28/Dec/20

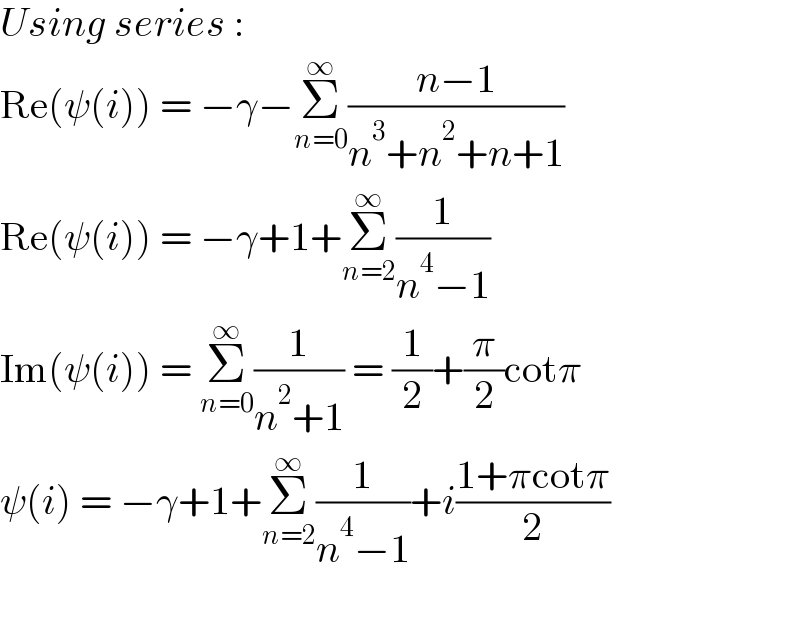
Using series : Re(ψ(i)) = −γ−Σ_(n=0) ^∞ ((n−1)/(n^3 +n^2 +n+1)) Re(ψ(i)) = −γ+1+Σ_(n=2) ^∞ (1/(n^4 −1)) Im(ψ(i)) = Σ_(n=0) ^∞ (1/(n^2 +1)) = (1/2)+(π/2)cotπ ψ(i) = −γ+1+Σ_(n=2) ^∞ (1/(n^4 −1))+i((1+πcotπ)/2)

$${Using}\:{series}\:: \\ $$$$\mathrm{Re}\left(\psi\left({i}\right)\right)\:=\:−\gamma−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{n}−\mathrm{1}}{{n}^{\mathrm{3}} +{n}^{\mathrm{2}} +{n}+\mathrm{1}} \\ $$$$\mathrm{Re}\left(\psi\left({i}\right)\right)\:=\:−\gamma+\mathrm{1}+\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{4}} −\mathrm{1}} \\ $$$$\mathrm{Im}\left(\psi\left({i}\right)\right)\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} +\mathrm{1}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}+\frac{\pi}{\mathrm{2}}\mathrm{cot}\pi \\ $$$$\psi\left({i}\right)\:=\:−\gamma+\mathrm{1}+\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{4}} −\mathrm{1}}+{i}\frac{\mathrm{1}+\pi\mathrm{cot}\pi}{\mathrm{2}} \\ $$$$ \\ $$

Commented by mnjuly1970 last updated on 28/Dec/20

thank you ...

$${thank}\:{you}\:... \\ $$

Answered by mindispower last updated on 28/Dec/20

Ψ(i)=−γ+Σ_(n≥1) ((1/(n+1))−(1/(n+i))) =−γ+Σ_(n≥0) ((1/(n+1))−((n−i)/(n^2 +1))) =−γ+Σ_(n≥0) ((−n+1)/(n^3 +n^2 +n+1))+iΣ_(n≥0) (1/(n^2 +1)) ReΨ(i)=−γ−Σ_(n≥0) ((n−1)/(n^3 +n^2 +n+1)) Im(Ψ(i))=Σ_(n≥0) (1/(n^2 +1))=(1/2)(Σ_(−∞) ^∞ (1/(n^2 +1))+1) =(1/2)(1−2Reπcoth(iπ).(1/(1−i))) =(1/2)(1−Re(πicoth(π).(1+i)) =(1/2)(1+πcotth(π)) Im(Ψ(i))=(1/2)+(π/2)coth(π) Re(Ψ(i))=−γ−Σ_(n≥1) ((n−1)/(n^3 +n^2 +n+1))..no close form in elementry function

$$\Psi\left({i}\right)=−\gamma+\underset{{n}\geqslant\mathrm{1}} {\sum}\left(\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{{n}+{i}}\right) \\ $$$$=−\gamma+\underset{{n}\geqslant\mathrm{0}} {\sum}\left(\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{{n}−{i}}{{n}^{\mathrm{2}} +\mathrm{1}}\right) \\ $$$$=−\gamma+\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{−{n}+\mathrm{1}}{{n}^{\mathrm{3}} +{n}^{\mathrm{2}} +{n}+\mathrm{1}}+{i}\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{{n}^{\mathrm{2}} +\mathrm{1}} \\ $$$${Re}\Psi\left({i}\right)=−\gamma−\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{{n}−\mathrm{1}}{{n}^{\mathrm{3}} +{n}^{\mathrm{2}} +{n}+\mathrm{1}} \\ $$$${Im}\left(\Psi\left({i}\right)\right)=\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{{n}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}}\left(\underset{−\infty} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} +\mathrm{1}}+\mathrm{1}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{2}{Re}\pi{coth}\left({i}\pi\right).\frac{\mathrm{1}}{\mathrm{1}−{i}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−{Re}\left(\pi{icoth}\left(\pi\right).\left(\mathrm{1}+{i}\right)\right)\right. \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\pi{cotth}\left(\pi\right)\right) \\ $$$${Im}\left(\Psi\left({i}\right)\right)=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\pi}{\mathrm{2}}{coth}\left(\pi\right) \\ $$$${Re}\left(\Psi\left({i}\right)\right)=−\gamma−\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{n}−\mathrm{1}}{{n}^{\mathrm{3}} +{n}^{\mathrm{2}} +{n}+\mathrm{1}}..{no}\:{close}\:{form}\: \\ $$$${in}\:{elementry}\:{function} \\ $$

Commented by mnjuly1970 last updated on 28/Dec/20

thank you so much sir power..

$${thank}\:{you}\:{so}\:{much}\:{sir}\:{power}.. \\ $$

Commented by mindispower last updated on 29/Dec/20

always pleasur sir

$${always}\:{pleasur}\:{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com