Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 127383 by Lordose last updated on 29/Dec/20

Is there any analytic proof of the result sin(x+y) = sin(x)cos(y) + sin(y)cos(x)

$$\mathrm{Is}\:\mathrm{there}\:\mathrm{any}\:\mathrm{analytic}\:\mathrm{proof}\:\mathrm{of}\:\mathrm{the}\:\mathrm{result} \\ $$$$\mathrm{sin}\left(\mathrm{x}+\mathrm{y}\right)\:=\:\mathrm{sin}\left(\mathrm{x}\right)\mathrm{cos}\left(\mathrm{y}\right)\:+\:\mathrm{sin}\left(\mathrm{y}\right)\mathrm{cos}\left(\mathrm{x}\right) \\ $$

Answered by bemath last updated on 29/Dec/20

Answered by liberty last updated on 29/Dec/20

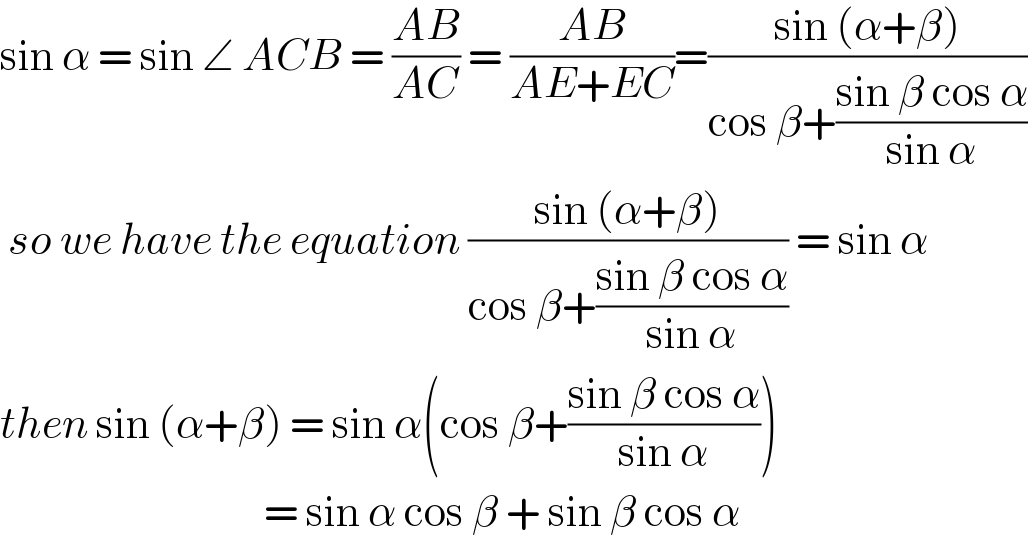
sin α = sin ∠ ACB = ((AB)/(AC)) = ((AB)/(AE+EC))=((sin (α+β))/(cos β+((sin β cos α)/(sin α)))) so we have the equation ((sin (α+β))/(cos β+((sin β cos α)/(sin α)))) = sin α then sin (α+β) = sin α(cos β+((sin β cos α)/(sin α))) = sin α cos β + sin β cos α

$$\mathrm{sin}\:\alpha\:=\:\mathrm{sin}\:\angle\:{ACB}\:=\:\frac{{AB}}{{AC}}\:=\:\frac{{AB}}{{AE}+{EC}}=\frac{\mathrm{sin}\:\left(\alpha+\beta\right)}{\mathrm{cos}\:\beta+\frac{\mathrm{sin}\:\beta\:\mathrm{cos}\:\alpha}{\mathrm{sin}\:\alpha}} \\ $$$$\:{so}\:{we}\:{have}\:{the}\:{equation}\:\frac{\mathrm{sin}\:\left(\alpha+\beta\right)}{\mathrm{cos}\:\beta+\frac{\mathrm{sin}\:\beta\:\mathrm{cos}\:\alpha}{\mathrm{sin}\:\alpha}}\:=\:\mathrm{sin}\:\alpha \\ $$$${then}\:\mathrm{sin}\:\left(\alpha+\beta\right)\:=\:\mathrm{sin}\:\alpha\left(\mathrm{cos}\:\beta+\frac{\mathrm{sin}\:\beta\:\mathrm{cos}\:\alpha}{\mathrm{sin}\:\alpha}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{sin}\:\alpha\:\mathrm{cos}\:\beta\:+\:\mathrm{sin}\:\beta\:\mathrm{cos}\:\alpha\: \\ $$

Commented by liberty last updated on 29/Dec/20

Answered by MJS_new last updated on 29/Dec/20

sin α =((e^(iα) −e^(−iα) )/(2i))∧cos α =((e^(iα) +e^(−iα) )/2) sin (x+y) =((e^(i(x+y)) −e^(−i(x+y)) )/(2i))=((e^(ix) e^(iy) −e^(−ix) e^(−iy) )/(2i))= [let e^(ix) =u∧e^(iy) =v] =((uv−(1/(uv)))/(2i))=((2uv−(2/(uv)))/(4i))= =((2uv+(u/v)−(u/v)+(v/u)−(v/u)−(2/(uv)))/(4i))= =((uv+(u/v)−(v/u)−(1/(uv)))/(4i))+((uv−(u/v)+(v/u)−(1/(uv)))/(4i))= (((u−(1/u))(v+(1/v)))/(4i))+(((u+(1/u))(v−(1/v)))/(4i))= [u=e^(ix) ∧v=e^(iy) ] =((e^(ix) −e^(−ix) )/(2i))×((e^(iy) +e^(−iy) )/2)+((e^(ix) +e^(−ix) )/2)×((e^(iy) −e^(−iy) )/(2i))= =sin x cos y +cos x sin y

$$\mathrm{sin}\:\alpha\:=\frac{\mathrm{e}^{\mathrm{i}\alpha} −\mathrm{e}^{−\mathrm{i}\alpha} }{\mathrm{2i}}\wedge\mathrm{cos}\:\alpha\:=\frac{\mathrm{e}^{\mathrm{i}\alpha} +\mathrm{e}^{−\mathrm{i}\alpha} }{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{sin}\:\left({x}+{y}\right)\:=\frac{\mathrm{e}^{\mathrm{i}\left({x}+{y}\right)} −\mathrm{e}^{−\mathrm{i}\left({x}+{y}\right)} }{\mathrm{2i}}=\frac{\mathrm{e}^{\mathrm{i}{x}} \mathrm{e}^{\mathrm{i}{y}} −\mathrm{e}^{−\mathrm{i}{x}} \mathrm{e}^{−\mathrm{i}{y}} }{\mathrm{2i}}= \\ $$$$\:\:\:\:\:\left[\mathrm{let}\:\mathrm{e}^{\mathrm{i}{x}} ={u}\wedge\mathrm{e}^{\mathrm{i}{y}} ={v}\right] \\ $$$$=\frac{{uv}−\frac{\mathrm{1}}{{uv}}}{\mathrm{2i}}=\frac{\mathrm{2}{uv}−\frac{\mathrm{2}}{{uv}}}{\mathrm{4i}}= \\ $$$$=\frac{\mathrm{2}{uv}+\frac{{u}}{{v}}−\frac{{u}}{{v}}+\frac{{v}}{{u}}−\frac{{v}}{{u}}−\frac{\mathrm{2}}{{uv}}}{\mathrm{4i}}= \\ $$$$=\frac{{uv}+\frac{{u}}{{v}}−\frac{{v}}{{u}}−\frac{\mathrm{1}}{{uv}}}{\mathrm{4i}}+\frac{{uv}−\frac{{u}}{{v}}+\frac{{v}}{{u}}−\frac{\mathrm{1}}{{uv}}}{\mathrm{4i}}= \\ $$$$\frac{\left({u}−\frac{\mathrm{1}}{{u}}\right)\left({v}+\frac{\mathrm{1}}{{v}}\right)}{\mathrm{4i}}+\frac{\left({u}+\frac{\mathrm{1}}{{u}}\right)\left({v}−\frac{\mathrm{1}}{{v}}\right)}{\mathrm{4i}}= \\ $$$$\:\:\:\:\:\left[{u}=\mathrm{e}^{\mathrm{i}{x}} \wedge{v}=\mathrm{e}^{\mathrm{i}{y}} \right] \\ $$$$=\frac{\mathrm{e}^{\mathrm{i}{x}} −\mathrm{e}^{−\mathrm{i}{x}} }{\mathrm{2i}}×\frac{\mathrm{e}^{\mathrm{i}{y}} +\mathrm{e}^{−\mathrm{i}{y}} }{\mathrm{2}}+\frac{\mathrm{e}^{\mathrm{i}{x}} +\mathrm{e}^{−\mathrm{i}{x}} }{\mathrm{2}}×\frac{\mathrm{e}^{\mathrm{i}{y}} −\mathrm{e}^{−\mathrm{i}{y}} }{\mathrm{2i}}= \\ $$$$=\mathrm{sin}\:{x}\:\mathrm{cos}\:{y}\:+\mathrm{cos}\:{x}\:\mathrm{sin}\:{y} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com